Стаффорд Бир:
Мозг Фирмы.
Часть I. Концептуальные компоненты.
Глава 5. Иерархия управления

Дискуссия, начатая в предыдущей главе, нуждается в продолжении. Она касалась эвристических методов, которые, как представляется, единственно способны организовать системы, названные нами немыслимыми. Был показан принцип работы устройства управления ими. Это алгедоническая цепь, содержащая алгоритм, порождающий эвристику. Вместе с тем было показано, что необходимый для этого алгоритм можно составить только на метаязыке. Это означает, что необходимо наличие системы второго порядка, связанной и соединённой с первой своей алгедонической цепью. Процесс продолжается до тех пор, пока не образуется командная иерархия, а он может продолжаться бесконечно. Логически можно строго доказать, что вся система в целом требует бесконечного числа метаязыков; и нельзя завершить их создание. Тогда, следовательно, нам рано или поздно придётся остановиться — без всякого логического основания — на наивысшей метасистеме как её вершине.

Такой неутешительный вывод не представляет, однако, ничего большего, чем параллель с обычными фактами существования любой организации. В деловом мире отделы координируются подразделениями, подразделения координируются отделениями, а отделения — гигантскими корпорациями. Различные уровни такого управления в значительной степени автономны, а управление ими в основном осуществляется алгедонически. (Об этом подробнее будет сказано в части II.) Глава корпорации сам смотрит наверх, на метасистему, называемую отраслью промышленности, и выше, на метасистему, называемую правительством. Обе они связаны с его корпорацией алгедонической цепью. И хотя довольно просто предвидеть остальную иерархию вплоть до системы космического масштаба, на практике мы удовлетворяемся вышестоящим уровнем управления как конечным судьёй наших дел. Никто из нас не в состоянии влиять более чем на одну или две системы выше нашей, и поэтому обычно мы принимаем алгедонический результат деятельности вышестоящего уровня как говорящий на языке «приказа».

Интересно начать анализ структур иерархического управления, задавшись вопросом о базисных решающих элементах, которые в общем случае формируют и отдают команды. Если рассматривать самую совершенную систему управления в природе — головной мозг человека, то элементарную ячейку управления можно представить в виде отдельной нервной клетки — нейрона. В промышленности или в правительстве, фактически в любой тесно связанной социальной группе, таким элементом является любой начальник, любой руководитель.

Как нейрон, так и руководитель призваны выполнять одну единственную фундаментальную роль — решать. В случае нейрона импульс может либо задействовать выходящий из него нерв (аксон), либо нет. Для управляющего фундаментальная задача тоже сводится к тому, чтобы сказать да или нет. Верно, что руководители не тратят всю свою жизнь на произнесение только этих двух слов; они могут вообще никогда их не произносить. Тем не менее в этом их роль, а замены, нюансы типа «могу посоветовать», «вероятно, Вам бы лучше…» — принятые в обществе формы вежливо сказать да или нет.

Чтобы выбрать между да и нет, между 0 и 1, решающий элемент вынужден установить порог принятия решения. Можно представить, что он выдаёт сообщение 0 до тех пор, пока обстоятельства не заставят его сообщить о скачке в 1. Это будет разрешающий тип управления, при котором решающий элемент ничего не делает, пока обстоятельства не заставят его действовать. Он и не должен реагировать на всякий случайный импульс или шум, и это обстоятельство предопределяет необходимость в таком пороге. Сверхчувствительный нейрон быстро сведёт с ума как человека, так и фирму. Когда что-то реально начинает происходить, решающий элемент накапливает тому свидетельства. Когда он убедится, что действительно произошло событие, требующее его действия, то есть иными словами, когда сумма внешних импульсов достигла порога, он срабатывает.

Сказанное здесь может показаться мелочью. Но я искал описание, которое было бы общим и для руководителя, и для нейрона. И если всё ранее сказанное имеет смысл, то можно перейти к общей теории систем, с тем чтобы описать порог чувствительности как функцию преобразования. Дан набор импульсов, которые, подчиняясь определённому критерию, преобразуются в 0 или 1 на выходе. Поскольку, как было показано в двух предыдущих главах, организации не могут надеяться на детализированное управление событиями сверху, лучше всего рассматривать функцию преобразования как обеспечивающую скромную степень алгедонического одобрения при нормальном состоянии системы. Так, если мы располагаем 20 алгедоническими каналами ввода, то, возможно, в 15 из них установлен уровень 1, когда дела идут нормально. Пять, уровень которых установлен на 0, представляют меру, с которой вся алгедоническая система обратной связи подвержена возможному административному вмешательству. Если события выйдут из-под контроля в системе более низкого уровня, то уровень всех 20 алгедонических каналов может оказаться нулевым, но если дела пойдут весьма успешно, то некоторые из первоначальных нулей могут перейти в единицы.

Предположим, однако, что сама функция преобразования оказалась неверной, то есть неверно учитывающей условия окружающей среды, в которой срабатывает или не срабатывает нейрон или руководитель. Конечно, такое суждение будет сделано метасистемой. Тогда, предположим, функция преобразования должна изменить свой знак, что никуда не годится; мы не можем позволить функции преобразования такого сальто-мортале на выходе, смены результата с 0 на 1 и обратно таким скачком просто потому, что окружающая среда несколько неустойчива. Было бы лучше постепенно изменять порог чувствительности так, чтобы решающий элемент соответственно изменял свою реакцию. Лучше всего понять это, если рассматривать серию суждений, при которых очевидно значимый результат на выходе получается более или менее резко и наблюдаются его последствия. Иначе говоря, сформировать обратную связь, которая приведёт к адаптации самой функции преобразования. Следует отметить, что некоторые условия окружающей среды могут потребовать большей чувствительности нейронов или руководителей, а другие её условия — её уменьшения.

Последнее относится к особому случаю теории управления, рассматриваемому в Главе 2. При этом на сенсорном входе и моторном выходе сохраняются афферентные и эфферентные импульсы соответственно. Сохраняется также анастомотик ретикулум, который мы не собираемся детально анализировать или подвергать управлению соответствующими для этого случая командами. Более того, его действия ясно продемонстрированы (пока что) на примере машины из дерева и меди в предыдущей главе.

Рассмотрим сенсорное устройство такой машины. У неё 10 контактов, которые собирают данные, передаваемые им из внешнего мира, представленного колесом рулетки. В своё время мы говорили, что таких контактов может быть хоть сотня. Конечно, может быть и любое произвольное число контактов, как угодно разбросанных по сенсориуму. Машина будет по-прежнему работать. Более того, предположим, что функция преобразования, представленная отношением числа контактов, находящихся на двух медных полосах А:В в любое данное время не является очень грубой. Можно представить себе в качестве примера химическую клетку, порог срабатывания которой представлен значением рН или какой-то электрической величиной, прочитанной от преобразователя на языке Мета–1 и усиленной или подавленной цепью связи.

В таком случае связь между входом и выходом проследить невозможно. Часть её (периферийная) по характеру дискретная — поток двоичных импульсов поступает (и распространяется) в высшей степени запутанную сеть линий. Проследить всё это достаточно трудно и фактически невозможно, если сеть будет непрерывно изменяться — линии могут атрофироваться или непостижимым образом включаться в работу или выключаться. Однако если их достаточно много, машина продолжит работу. Хуже того, внутриклеточная связь будет прослеживаться только на молекулярном уровне. Практически мы будем иметь дело со статистическим эффектом массы. Наиболее близкое описательное название, которое обозреватель может присвоить этой внутренней части нейрона, могло бы быть «аналоговое устройство», поскольку основной двоичный характер системы потерян. Как бы там ни было, в конечном счёте вся система связи и взаимодействие в ней могли бы служить отличным примером анастомотик ретикулум.

Как представляется, реальный живой нейрон выглядит весьма на это похожим. Более того, наше его описание достаточно хорошо соответствует и управляющему. При рассмотрении сути этого замечания опасайтесь путаницы в оценке различий в их разрешающей способности (в оптическом смысле). Мы рассматриваем нейрон (как естественный, так и искусственный) и управляющего как простой элемент решения в сети нейронов (мозг) или как человека (в обществе управляющих). Тот факт, что в мозгу управляющего содержится 10 миллиардов нейронов, не имеет значения для нашего сравнения. Тем не менее это интересное замечание, когда мы приступаем также к рассмотрению иерархии команд. Во всём этом наблюдается удивительная гомогенность, а собственный язык управляющего, очевидно, является метаязыком n-го порядка по отношению к машинному языку его собственных нейронов.

Кстати, если сенсориум изобретённой нами машины может быть представлен большим, возможно неизвестным, числом входов вместо первичных десяти, алгедоническая цепь сможет успешно работать и на менее точной основе. Мы говорили, что срабатывание цепи алгедонической обратной связи вызовет движение деревянного бруса, при котором контакт, один из десяти, переместится с пластины A на пластину В. Однако если число произвольно разбросанных контактов весьма велико, то это правило становится бессмысленным. Во всяком случае, нет никаких оснований, в силу которых алгедоническое движение должно быть дискретным, осуществляемым небольшими скачками. Давайте представим этот обусловленный процесс как своеобразное давление, под действием которого очень незначительно перемещается деревянный брус, при этом плавно исправляя ошибки. Теперь мы знаем, что алгедоническая функция сама определена метаязыковым решением, чем-то таким, что ценится высшим руководством. Какой бы ни была система, определяющая сигнал, алгедоническая цепь различает не только верен ли выданный зажегшейся лампочкой сигнал, но и насколько он верен или неверен. Давайте зафиксируем этот результат и используем его применительно к силе, двигающей деревянный брус. Обычно его перемещение невелико: вероятность А: В может измениться с 50:50 на 51:49. Если «неверный» ответ внезапно (металингвистически) становится опасным, давление будет продолжаться; отношение 50:50 может сразу же измениться на 99:1 (однако не на 100:0, поскольку это исключает возможность изменения соотношений). И вновь совершенно ясной становится аналогия действий управляющего и движения, с которым связано решение о поощрении или наказании.

Прежде чем переходить к рассмотрению действующих ступеней иерархий, уместно сделать общее замечание. Нас всегда учили представлять командные сети как специально созданные, располагающие узловыми пунктами, действующими в качестве переключателей, зависящими от обратной связи в инженерном смысле (см. Главу 2). Однако, во-первых, жизнеспособные системы фактически демонстрируют наличие в них скорее анастомотик ретикулум, чем надлежащим образом разработанной сети, элементы которой формируются и переформировываются самостоятельно в соответствующие структуры. Во-вторых, элементы, являющиеся узловыми пунктами, управляются меняющимися функциями преобразования; они лучше всего описываются как непрерывно модифицирующиеся условные вероятности, а не неизменные операторы, которые в представлении стандартной теории управления являются дифференциальными уравнениями. В-третьих, цепи обратной связи не просто устройства коррекции ошибок, которые приводят выходной результат в соответствие с «правильным» значением. Они являются алгедоническими цепями, идущими от систем высшего порядка, влияющими на первые два вида изменений. Но и в такой роли согласно стандартной теории управления главной функцией этих систем остаётся обратная связь.

Из того, что было до сих пор изложено, вытекает, что нейрофизиологическую и управляющую системы (если взять две жизнеспособные системы, которые, как оказалось, имеют много общего) легче всего понять, представляя именно с учётом сказанного, а их основные элементы — нейрон и управляющего — как работающих в соответствии с моделью, представленной в её самой простой форме деревянно-медной машины. Для облегчения дальнейших ссылок надо её назвать, и я выбрал в качестве имени алгедонод. Я знаю, насколько утомительно продолжать вводить новые для читателя названия, в особенности (как в данном случае) если я вынужден самих изобретать. Однако словарь, представляемый управляющим, поразительно ограничен. Здесь вводится понятие, определённое с той степенью глубины, с которой мне удалось это сделать. Решающий элемент в системе управления состоит в принципе из входящей (или афферентной) и выходной (или эфферентной) подсистемы информации, соединённой с помощью анастомотик ретикулум. Все эти три части системы управления были достаточно подробно определены ранее. Этот решающий элемент является узлом в сети решающих элементов, образующих систему управления. Но этот узел как решающий элемент обусловлен (в смысле путей его изучения) метасистемой, использующей эвристический метод поощрения и наказания, который мы назвали алгедоническим. Все это вместе является алгедонодом. Наша деревянно-медная машина — грубый его пример, но и нейрон мозга, и отдельный руководитель в числе членов правления — тоже алгедоноды.

Нашим следующим шагом будет попытка распространить принцип машины, представленной на Рис. № 10, на всю командную иерархию и посмотреть, как подобная машина работает. Пусть следующий вариант деревянно-медной машины состоит из 32 элементов, каждый из которых сам является алгедонодом. Если наши ряды из восьми алгедонодов представить так, как показано на Рис. № 11, то получится устройство, способное принимать восемь двоичных решений вместо одного.

Рисунок № 11.

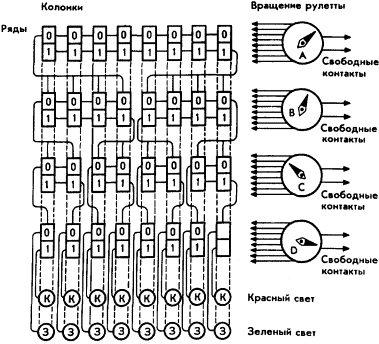
(Никакой мистики в этих числах нет — они выбраны просто для удобства.) Нижний ряд выглядит как восемь отдельных алгедонодов, на их выходе остаётся знакомая нам пара красного и зелёного света. Результат зажигания (выход) теперь кроется в первых трёх рядах, а двоичный выходной результат каждого алгедонода служит для выбора следующей группы элементов, которые тогда будут задействованы. На правой стороне рисунка показаны четыре рулетки в произвольных положениях, каждое из которых представляет неизвестный входной сигнал из внешнего мира.

Вращение четырёх, рулеток отражает «состояние внешнего мира». Легко видеть, что если каждое колесо рулетки располагает числами положений от 0 до 9, то общее число выходных состояний составит 10 000. (Представьте себе результат деятельности банка игральных костей, который фиксирует любую цифру между 0000 и 9999.) Имеется восемь контактов, связанных с входом А, на восьми колонках медных полос, и они поочерёдно находятся в состоянии 0 или 1 своего ряда. (Их соединения не показаны на рисунке, поскольку они слишком усложнили бы его, однако позднее они будут приведены на Рис. № 12.) Два контакта из десяти на колесе рулетки оставлены свободными в соответствии с законами мутации, исследованными нами ранее (как обходящие логику системы). Первый ряд алгедонодов тогда выбирает либо правую, либо левую группу из четырёх алгедонодов второго ряда. Один из свободных контактов направлен прямо к каждой из этих групп. Таково начальное условие игры, при котором точно соблюдается вероятность 50:50, что первый ряд задействует либо правую, либо левую группу из четырёх алгедонодов во втором ряду.

Рисунок № 12.

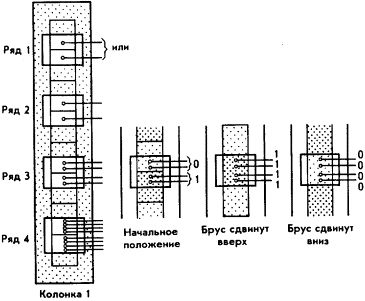
Во втором ряду тоже восемь контактов, представляющих случайный вход В. Они организованы так, что состояния как 0, так и 1 отражены каждым алгедонодом в каждой группе из четырёх алгедонодов. Это значит, что у нас всего 16 контактов и любой вход В задействует два из них — один в левой и один в правой группе. Однако решение первого ряда уже исключило одну из групп. Тогда ряд 2 задействует пару алгедонодов в ряду 3 либо через эту систему, либо (как и прежде) напрямую через два свободных входа. Для выбора остаются две пары либо из правой, либо из левой двойной группы в зависимости от решения ряда 2. Какая из этих пар будет задействована, зависит от положения рулетки С. В ряду 3 у нас четыре контакта к каждому из алгедонодов — два в положении 0 и два в положении 1, снова организованных в параллель. Таким образом, к ряду 3 сработают 32 контакта и только восемь из них (плюс два свободных для входа С) имеют отношение к третьему решению, поскольку три из четырёх пар ряда 3 уже исключены. Ряд 3 теперь определит, какой из алгедонодов в ряду 4 будет задействован.

Ряд 4 принимает окончательное решение, основанное на положении рулетки D. На этот раз все восемь контактов организованы в параллель на каждом алгедоноде (к этому моменту, следовательно, состоится 64 соединения), четыре из которых в положении 0 и четыре в положении 1. Ряд 3 решает, какую колонку задействовать, а ряд 4 решает, будет ли зажжён зелёный или красный свет. Повторим, что два резервных импульса, на этот раз от рулетки D, будут проходить прямо к той или другой лампочке.

Поскольку согласно исходным условиям весь наш ретикулум основан на 32 алгедонодах, предлагающих равное число значений 0 и 1, так сказать, на медных полосах, то результат игры полностью непредсказуем. Запустим все четыре рулетки. Они случайно задействуют контакт в своём ряду и каждый из рядов наполовину тоже случайно сокращает разнообразие следующего ряда. Любой из восьми парных контактов может сработать при равных вероятностях загорания зелёной или красной лампочки. Таким образом, мы располагаем двумя возможными двоичными решениями в физическом смысле: у нас имеется четыре ряда алгедонодов, которые, следовательно, способны принимать решения, осуществляя выбор из 2⁴ = 16 результатов на выходе, то есть из 16 вариантов зажигания лампочек. Теория, описывающая такой процесс, была изложена в Главе 3.

Чтобы заставить такую машину работать как электромеханическое устройство, потребуются «принимающие решения» реле, а эти реле будут срабатывать при совпадении поступления входного импульса данного ряда с выходным импульсом, определённым в предыдущем ряду. Одно реле необходимо как выходное для ряда 1; оно будет осуществлять подключение к одной из двух групп алгедонодов в ряду 2. Выходной результат рядов 2 и 3, очевидно, требует двух и четырёх реле соответственно. Ряду 4 не нужны никакие реле, поскольку он прямо зажигает лампочки. Из этого следует, что требуется 2^{n — 1} — 1 фактически решающих элементов (реле). В нашем случае когда, n = 4, число состояний на выходе 2⁴ = 16 и число реле составляет 2³ — 1 = 7. Если степень неопределённости увеличить на 1, то получим n = 5,2⁵ = 32 состояния на выходе, 2⁴ — 1 = 15 реле и, следовательно, 16 колонок. Но такая машина будет дополнительно воспринимать выходной сигнал Е и может управлять 100 000 состояниями мира.

Хорошо сказать «может управлять», подразумевая, что ретикулум, связывающий вход и выход, не перегружен, что он может отличать один набор реакций от другого. Но выражение «может управлять» до сих пор означало «производить случайный результат», а для этого не стоило бы создавать такую машину. Следующим шагом будет соединение алгедонодов вместе по колонкам. Одна вертикальная колонка такой машины приведена на Рис. № 12, чтобы можно было показать, как она работает. Следует отметить, что уже можно показать иерархические соединения, которые мы только что обсуждали. В каждой колонке восемь медных полос — все они смонтированы на одном деревянном брусе. Они изолированы одна от другой и меняют состояние 0 и 1 вдоль колонки. Фактически, конечно, здесь остаётся (в силу электрических соединений) четыре набора алгедонодов. Как показано на Рис. № 12, они помечены, поскольку некоторое число «свободных» медных шин 0 или 1 необходимо, когда деревянный брус перемещается вверх или вниз.

Теперь становится возможной работа цепи алгедонической обратной связи. Для начала рассмотрим её в самом общем виде. Если зажигается не та лампочка, которая нужна, наказание будет суровым. Вся медная полоса, которая обеспечила подобный результат в ряду 4, будет исключена и во всех остальных рядах, принадлежащих данной колонке. Но не будет изменений в соседних колонках, поскольку в них полосы не передвигали. Следовательно, баланс вероятностей состояний всей машины изменится весьма интересным образом. Рассмотрим только одну пару лампочек — ту, которая зажигается колонкой алгедонода ряда 4. Вероятность того, что, к примеру, загорится красная лампочка, составит теперь 9:1. (Все восемь контактов находятся на одной медной пластине, один запасной канал ввода соединён непосредственно с красной лампочкой, а другой — с зелёной.)

Однако вероятность того, что этот полностью адаптировавшийся алгедонод (ряд 4 в колонке 1) будет вообще выбран, тоже изменилась. Его выбор производится алгедонодами ряда 3 из колонок 1 и 2. Тогда вероятность того, что именно эта пара выберет либо колонку 1, либо колонку 2 ряда 4, была 5:5. Но, поскольку брус колонки 1 переместился на целый ряд, состояния двух из четырёх выбранных нами зон (0 и 1, 0 и 1 в двух колонках) изменились на 0. Тогда три из них будут находиться в состоянии 0 и один в состоянии 1. При этом шесть из восьми контактов, находящихся на этой пластине, будут соединены с 0 и только два с 1. С учётом наличия двух свободных входов вероятность того, что ряд 3 выберет эту колонку в ряду 4, изменится с 5:5 на 7:3.

Продвигаясь в обратном порядке по дереву решений, подойдём к ряду 2, который содержит четвёрку алгедонодов. Здесь первично решение принималось с помощью восьми контактов, соединённых с восемью зонами (четыре нуля и четыре единицы), но теперь баланс нарушен так, что там, где были нули, и там, где были единицы, в колонке 1 считываются только нули. Теперь у нас пять нулевых и три единичных зоны. С учётом свободных каналов вероятность выбора в этом случае станет равной 6:4. Переходя к ряду 1 и рассматривая вероятность, с которой будет выбрана эта четвёрка в ряду 2, мы столкнёмся с 16 медными зонами, из которых только восемь касаются контактов. Такое положение формально эквивалентно тому, что было в ряду 2.

Теперь становится понятным, каковы вероятности всего дерева решений, определяющих включение лампочек колонки 1. В начальном положении каждый ряд обусловливает вероятность 0,5 того что загорится в конечном счёте красная лампочка. Вероятность того что это так и будет, составляет, следовательно, 0,5⁴ = 0,0625 или одну шестнадцатую. Поскольку у нас всего 16 лампочек и исходное состояние машины равно вероятно, именно этого следовало ожидать. Но после того, как мы произвели грубую алгедоническую настройку в колонке 1, вероятности стали равными: 0,6 для ряда 1, 0,6 для ряда 2, 0,7 для ряд в 3 и 0,9 для ряда 4. Общая вероятность составит 0,2268 — между одной пятой и четвёртой. Вероятность того, что загорится Зелёная лампочка в колонке 1, составит 0,6 × 0,6 × 0,7 (поскольку порядок выбора в первых трёх рядах одинаков) × 0,1. Тогда результат будет 0,0252, то есть нужная лампочка загорится однажды при сорока попытках.

Дальнейшее понимание того, что происходит, становится довольно затруднительным. Грубая алгедоническая обратная связь в колонке 2 на втором туре игры даст вероятность 9:1 зажигания нужной лампочки в ряду 4. Но, поскольку ряд 2 выбрал левую пару алгедонода в ряду 3, мы получим вероятность 0,9 правильного ответа в общем так как неважно, выберет ли ряд 3 колонку 1 или 2 в ряду 4. Более того, поскольку алгедоническая обратная связь приводит к усилению (или ослаблению) её эффекта по всей иерархии, ряд 1 наиболее вероятно выберет левую четвёрку в ряду 2, а он наиболее вероятно выберет левую пару в ряду 3.

Не имеет смысла дальше описывать теоретическое изменение вероятностей в этой машине, поскольку мы уже слишком упростили это и без того простое устройство. Если алгедоническая обратная связь не очень груба (а к чему ей быть такой?), то число вариантов перемещения медных пластин может быть весьма большим всё это существенно усложнит теорию. Более того, мы не намерены в действительности ограничиваться восемью контактами в ряду: их может быть довольно много и как угодно произвольно-расположенных Это ещё более усложнит расчёт вероятностей, но это не должно нас смущать. Важно другое: математический инструмент становится довольно произвольным. Точнее, вероятностная функция преобразования для любого состояния множества этих 32 элементов в высшей степени сложна и не стоит того, чтобы в ней здесь разбираться Достаточно небольшого развития, небольшого уточнения конструкции и наша машина становится настоящим анастомотик ретикулумом. Самое странное, что она выполняет эту роль. Она сводит 10 000 комбинаций состояний на входе к 16 состояниям на выходе, так что наблюдатель, говорящий на языке Мета–1, считает результат её работы полезным. Таким образом, машина обучается правильному поведению. Если окружающая среда изменяется (исходя из метасистемных критериев успеха), машина быстро приспосабливается к этим переменам. Но именно этого мы и хотели.

Если это понятно, то возникает следующий вопрос: как такая машина может стать полезной? Во-первых, наш искусственный пример чисто, иллюстративен, и даже в таком случае он довольно труден для понимания. Я реализовал его на картоне так, чтобы можно было подсчитывать результаты игры. Он достаточно хорошо соответствовал своему назначению, но его демонстрация занимала слишком много времени. Я пытался также сделать электрический вариант машины на тех же принципах, но здесь возникла масса трудностей механического и электрического характера. В частности, электрические цепи, как оказалось, требуют множества соединений, а для логического управления переключениями — использования диодов. Но и тогда эта простая машина, работу которой, как я по-прежнему считаю, легче понять концептуально, выглядела страшно сложной, а это губит весь её иллюстративный смысл, хотя и даёт представление о возможности управления разнообразием реакции алгедонода. Полноразмерная демонстрационная модель, весьма впечатляющая, была в конце концов построена фирмой Macnamara Ltd и Н. Гриффином из Экстерского университета. Последнему я выражаю свою благодарность.

Таково то, о чём мы должны подумать в терминах значительно более совершенной техники. Перед нами две альтернативы, и выбор между ними, как увидим позже, весьма важен. Первая связана с программированием универсальной ЭВМ, обеспечивающим именно такое её поведение. Вторая связана с созданием специальной системы, использующей физику твёрдого тела. Но значительно важнее, чем все эти технические средства, признание существования алгедонодов, поскольку именно такого рода сложные перестановки производятся внутри групп управляющих — с использованием людей в качестве элементов.