Стаффорд Бир:
Мозг Фирмы.
Часть I. Концептуальные компоненты.
Глава 2. Общие понятия и терминология

Чтобы понять сущность кибернетики больших систем управления, нам неизбежно придётся порвать с общим стилем мышления, использованным в Главе 1. Если существуют принципы управления, то следует начать с их точного определения. Это будет сделано исходя из того, что общие понятия и терминология, известные в классической науке управления, мало чем нам помогут. Следовательно, в этой главе начнётся обсуждение систем и управления ими на новом языке, без особых ссылок на деятельность фирм. Идея сводится к тому, чтобы сесть и подумать всерьёз. Что такое, собственно говоря, управление?

Первый принцип управления сводится к тому, что управляющий является частью управляемой им системы. Управляющий не является человеком, посаженным над системой высшей властью, который в дальнейшем реализует свои полномочия. В любой системе, говорим ли мы о популяции животных или внутренних функциях живого организма, функции управления распределены по всей её архитектуре. Управление совершенно невозможно отделить от организма, но его существование вытекает из поведения самой системы. Более того, управление совершенствуется с ростом системы, и если оглянуться на историю, то станет видно, что и управляющий развивался вместе с системой.

По этой причине лучше спрашивать о том, как система узнает о себе и своём состоянии, чем спрашивать, как то же самое узнает управляющий. Я полагаю, что нам не следует рисковать, отождествляя систему с личностью или с чем-то другим, лучше принять за систему те границы, в которых её различает обозреватель. Будем далее определять состояние системы по её поведению, то есть выделять в поведении то, что можно считать типичным для любой действующей системы. Примем систему как данное. Определим набор частей как систему, поскольку все её части выступают как действующие в единстве. Примем обычную деятельность системы за примерное отображение её естественной динамики. Иначе говоря, рассмотрим тот случай, когда части системы действуют типичным образом. Далее посмотрим, что произойдёт, если мы вмешаемся — воткнем палку в систему, прикрикнем на неё или изменим температуру её окружающей среды. Если система как-то ответит на эти стимулы, то можно сказать, что это действующая система. Заметьте, нам не нужно говорить, что система реагирует на стимулы, поскольку это требует целенаправленных действий по отношению к окружающему миру. Всё, что мы узнали из этого эксперимента, сводится к тому, что система чувствует вмешательство в неё. Это различие очень важно.

Подобное объяснение вызывает новый вопрос: что считать ответом на стимулы? Если мы вмешаемся в работу автомобильного двигателя, выключив зажигание, то будет ли верным заявить, что система реагировала остановом? Нет, поскольку мы разрушили динамическую систему, изучаемую нами, а не внесли в неё стимулы. Если мы выстрелом ранили животное, оно умрёт по той же причине. В равной мере если мы бросили спичку на блок цилиндров автомобильного мотора или на спину слону, то ничего не произойдёт. На этот раз потому, что наше вмешательство нельзя признать стимулом.

Нетрудно уловить смысл сказанного. Ясно, что за стимул следует принимать такое вмешательство, которое так или иначе отразится на действиях системы, будучи не слишком незначительным, чтобы не отразиться на её деятельности, и не слишком сильным, чтобы её разрушить. За реакцию системы примем некоторое её изменение, имеющее смысл только результата воздействия использованного стимула. Если система изменится произвольно при введении в неё того, что мы приняли за стимул, то, вероятно, какие-то изменения последуют. Кот, не покинувший комнату после того как он увидел плакат «Поди прочь», не отреагировал на содержание надписи, и, следовательно, по нашему определению, для него такой плакат не является стимулом. Но мы вполне можем натренировать кота покидать комнату всякий раз, когда он увидит этот плакат. Если он станет всякий раз убегать из комнаты, то нам придётся оставить идею о случайном совпадении и говорить о его реакции на стимул, то есть о коте как о действующей системе.

Из этого рассуждения вытекает несколько важных принципов управления. Стимулом является то, что изменяет работу системы. Реакция системы есть её действие, которое должно интерпретироваться в качестве следствия стимулов. В общем, это означает, что система избегает стимулов или как-то по-другому противодействует стимулам, нарушающим её деятельность, и воспринимает или стремится усилить стимулы, способствующие её деятельности. Следует отметить, что мы считаем очевидным, что наблюдаемые нами действия системы не являются случайными. Такое суждение зависит от того, насколько сильно влияет вмешательство на качественные показатели системы (что может ввести в заблуждение) или на высоконадёжные показатели их повторяемости (это является научным критерием). Система, подтверждающая такое её поведение, является действенной, по крайней мере до известной степени. Если она подтверждает такое своё поведение при всех обстоятельствах, мы будем называть её действующей без всякого сомнения или оговорок. Это не будет безнадёжно антинаучным суждением, поскольку вселенная подчиняется вероятностным, а не абсолютным законам.

В физике, генетике, общественных науках мы полагаемся на описания и даже на законы, которые основаны на равной вероятности случайностей. Только в специальных или искусственно созданных областях, таких как инженер не может создать машину или какую-либо конструкцию, защищённую от неизвестных, непредвиденных помех, но может создать защищённую только от тех, которые указаны заранее. Нам говорят, что мы должны определить, что считается стабильной работой машины, а затем перечислить по порядку помехи, которые считаются нарушающими стабильность её работы. Тогда и только тогда мы будем в состоянии создать или запрограммировать систему, которая «правильно» воспримет помеху в её работе. Все это неверно. То, в чём действительно нуждается система, и это все, в чём она нуждается, так это в способе измерения её собственной внутренней тенденции отклоняться от стабильного состояния, а также в наборе правил проведения экспериментальной проверки её реакций, которые возвращают её к внутреннему равновесию. Следовательно, нет нужды знать наперёд, что вызовет нарушение работы системы, как нет нужды знать, что её нарушило. Вполне достаточно быть уверенным в том, что что-то случилось, классифицировать это нарушение и быть в состоянии изменить внутреннее состояние так, чтобы нарушение исчезло.

Система, которая может выполнить это, которая может справиться со случайным и непредвиденным вмешательством, известна в кибернетике как сверхстабильная система (по классификации Эшби). Например, можно представить себе устойчиво работающий компьютер, который в случае пожара в здании будет продолжать отщелкивать цифры, даже когда начнут плавиться его части. Можно подумать, что для защиты от подобного риска конструктор должен установить температурные датчики. Ничего подобного. Любой ультраустойчивый компьютер должен обнаруживать не пожар (обходиться без термометров), а «нарушение работы», поскольку внутреннее контрольное устройство должно показывать, что счёт стал неверен. Компьютеру тогда следовало бы привести в движение свои колеса и просто покинуть горящее здание. В таком случае люди могут подумать, что компьютер в состоянии «почуять» пожар, и вновь ошибутся. Разумное поведение часто основывается на простых механизмах, вроде только что упомянутого, которые вводят нас в заблуждение, заставляя думать, что они основаны на более глубоком понимании обстоятельств. Простейшая версия управляющего устройства, управляющей функции системы, которую можно себе представить, выглядит тогда так, как показано на Рис. № 6.

Сенсорное устройство (прямоугольник на Рис. № 6.), входящее в систему, может регистрировать наличие стимулов и классифицировать их. Управляющее устройство в нём должно либо усиливать (+), либо уменьшать (-) действие стимулов в зависимости от того, помогают они деятельности системы в целом или нарушают её. Для этого они включают и заставляют срабатывать точки А или В, которые далее предпринимают действия в зависимости от характера стимулов.

Чтобы выбрать положение переключателя (точку А или В), управляющее устройство должно сравнить ожидаемый результат эффекта своего выбора по критерию стабильности системы. Его простейшая стратегия для этого заключается в том, чтобы двинуться немного в сторону уменьшения, а затем немного в сторону усиления стимула, сопоставить получаемые результаты по своим критериям и затем твёрдо установить переключатель. Если система будет экспериментировать слишком долго, то она начнёт раскачиваться. В технике это называется рысканием, в психологии — атаксией. Все системы подвержены этой болезни. Если таково простейшее устройство управления, то теперь следует убедиться в том, что мы достаточно глубоко понимаем это, и овладеть основной терминологией, обходимой для её изучения.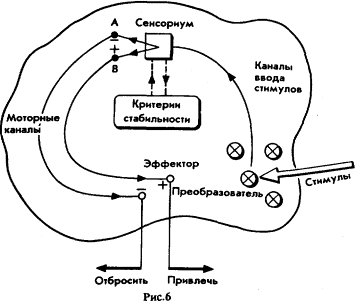

Стимулы, как было показано, возникают вне системы. Стимул может возникнуть и по внутренним причинам, но наше утверждение сохраняет силу — должно быть устройство, регистрирующее, что что-то произошло, и переводить происшедшее, каким бы оно ни было, в термины, имеющие смысл для управляющего устройства. Такое устройство есть часть системы — оно является не стимулом, а тем, что его обнаруживает. Оно называется преобразователем, то есть устройством, которое следит за стимулами для всей системы (оно помечено на Рис. № 6 в круге крестом). В систему, вероятно, входит один сенсориум, одно сенсорное устройство, но много преобразователей. Фактически, основная классификация стимулов происходит в самом начале и сводится к тому, чтобы разобраться, какой из преобразователей стимулировался.

Когда преобразователь сработал, сообщение о стимуле поступило в систему. Канал, по которому сообщение о стимулах поступает в систему, называется сенсорным каналом ввода. Эти сообщения являются сенсорными входными данными. Другая половина цепи управления, её замыкающая, является моторным каналом выхода (МОС). Соответствующий «мотор» связан с выходом, потому что выходные данные имеют смысл постольку, поскольку выходной сигнал вызывает действия. Например, в психологии нервы, представляющие выходные каналы, как говорят, передают «эффекторные» импульсы [которые могут быть стимулирующими либо ингибиторными (подавляющими): или +, или], тогда как сенсорный выход является «аффекторным». Таким образом, моторный выход ведёт к эффектам (пустая цепь на Рис. № 6), способности действовать в зависимости от стимулов. В простом случае один из них побуждает систему действовать согласно стимулам, другой — избавляться от них. Тогда, заметьте, пожалуйста, системе безразлично, что собственно вмешивается в неё.

Действующие в реальной жизни системы управления, конечно, намного богаче; масса импульсов пробегает через огромное число входных и выходных каналов. Это справедливо как в отношении организма человека, так и в отношении управленческих ситуаций. Этот факт не меняет базовой структуры сенсорных и моторных узлов в цепи управления; однако при рассмотрении операций переключения, которые подготавливают решения, мы должны принимать во внимание то, что в больших комплексных системах этот процесс никогда не сводится к столь простому переключению, как в нашей схеме (Рис. № 6).

В частном случае управления техническими средствами такая процедура переключения вполне понятна. Закономерность, отображающая такую процедуру, известна как функция преобразования, поскольку она математически указывает, какого сорта преобразования происходят между сенсорными и моторными узлами в цепи управления. Функция преобразования математически описывается дифференциальным уравнением и может быть весьма сложной. Сложность возникает потому, что характер реакции системы часто определяется диапазоном стимулирования, вызванного данным стимулом или частотой, с которой происходит стимулирование. В живых системах управления самым наглядным примером осуществления функции преобразования является деятельность нейрона или отдельной нервной клетки. Как утверждает Маккулох, функция преобразования в этом случае будет весьма сложной и описывается нелинейным дифференциальным уравнением восьмого порядка. Мозг человека состоит, вероятно, из 10 000 000 000 нейронов, и, насколько мы знаем, нет двух из них, функции преобразования которых были бы одинаковы. Мы столкнёмся с проблемой именно такого порядка при обсуждении функции преобразования руководителя. Решение, принимаемое в деловом мире, может касаться десятка руководителей, но это просто в сравнении с несколькими тысячами нейронов, функцию преобразования, управляющую нейронами, совершенно невозможно составить (если бы в этом было дело), поскольку она есть некоторая сумма взаимодействующих нейронов мозга. И нам это известно.

Дальнейшее ещё сложнее. При рассмотрении управления системой я целом, что является нашей конечной целью, мы вполне можем столкнуться с тем, что не удастся даже опознать отдельные входные и выходные каналы, а удастся идентифицировать лишьих целые связки ещё меньше наши возможности в отношении идентификации индивидуальных переключателей, преобразующие функции которых по этой причине не могут быть исследованы и ещё менее могут быть измерены. Тому есть существенные причины, обусловленные физиологическими структурами, такими как нервная система, и в социальных структурах, таких как корпорации и фирмы. В подобных случаях сенсорные входные данные поступают в сенсориум распределённо, а триггеры моторных действий тоже распределены широко и достаточно плотно не только по всей периферии системы, но и между точками А и В, о которых мы ранее упомянули. Проблема переключения, следовательно, охватывает весь набор входящих и весь набор выходящих импульсов. Следовательно, вместо одного переключателя между ними необходимо иметь сложную соединительную сеть. Такая сеть называется по латыни reticulum (сеточка, сетчатое образование), а её кибернетический вариант называется anastomotic. Это указывает на тот факт, что множество ветвей такой сети взаимодействуют целесообразно, но невозможно разобраться в том, как поступает сигнал в ретикулум. Этот термин просто означает что каналы вывода заканчиваются как дельта реки — множество потоков вливается в море и такие потоки, кроме того, часто переплетаются один с другим. Нет никакой возможности проследить, каким путём данная пригоршня воды попадает в море, как нет способа указать на то, из какого протока или источника она туда поступает.

Весьма важно усвоить это замечание об анастомотик ретикулум, поскольку процесс принятия решения как в организме человека, так и в сообществе руководителей осуществляется именно так. Мы видим информацию, которая была получена, видим предпринятые действия, эффекторные и аффекторные каналы, через которые эти меры осуществлялись, и только.

В этих условиях разумно перейти к электрической модели и попытаться построить систему переключателей, лежащую в основе цепи принятия решений. Более того, при рассмотрении Рис. № 6 казалось разумным представить эти соединения как переключатели (А и В). Так можно было поступить, поскольку мы рассматривали простейший случай. Без сомнения, бывают простые случаи и в управлении, когда управляющий, отвечая по телефону, говорит, что следует взять курс А или В — решение принято, и он кладёт трубку. В подобных случаях функция преобразования может быть выражена через минимизацию стоимости решения. Но это тривиальный случай. Обычно также трудно сказать, какие внутренние причины повлияют на группу руководителей, принимающих решение о том, как проследить путь воды в дельте реки. Поэтому, чтобы сделать модель более реальной, мы должны видоизменить главную цепь (Рис. № 6) и представить её, как показано на Рис. № 7.

Рисунок № 7.

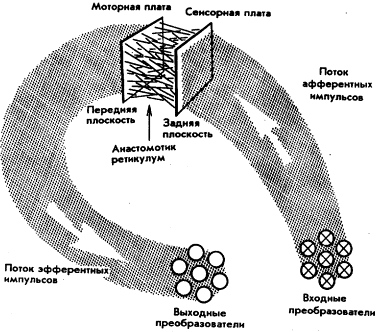
Применительно к этому новому варианту модели важно подчеркнуть следующее: стимулы возбуждают целую колонию входных преобразователей или сенсоров, а реакция системы осуществляется через целую колонию выходных преобразователей (или эффекторов). Оба этих набора преобразователей служат передатчиками импульсов через множество каналов. Сенсориум и связанный с ним переключатель заменены своего рода коробкой, имеющей сенсорную панель сзади и моторную панель спереди. Эти панели соединены своеобразной сетью переключающей системы, которую мы назвали анастомотик ретикулум.

Всё сказанное в этой главе до сих пор касалось управления большими комплексными системами исходя из первых принципов, хотя введённые термины имели явно биологический оттенок. Был упомянут также инженер-автоматчик, но в основном с тем, чтобы сказать, что он не в состоянии чем-то помочь нам! Однако теперь он снова выступает на авансцену, чтобы ввести новый термин — наиболее важную концепцию из всех — обратную связь. Прежде всего следует отметить, что было бы ошибкой принять связь между стимулом и ответной реакцией за систему обратной связи. Этот термин стал настолько вольно использоваться в ряде мест, что почти всякая реакция на любое действие принимается за обратную связь. Содержание этого термина следует вскрыть с известной осторожностью, поскольку он относится к фундаментальным понятиям кибернетики. Для его объяснения нам придётся привести небольшое математическое описание в самой общей форме в надежде на то, что это поможет правильно понять термин даже читателям, далёким от математики.

В системе есть входные и выходные сигналы. То, что происходит внутри системы и превращает первое во второе, уже было названо преобразованием и описывается функцией преобразования. В технике управления, как говорилось, функция преобразования описывается дифференциальным уравнением, которое определяет скорость преобразования во времени входных величин в выходные. Оператор в этом преобразовании обычно обозначается буквой «р». Нет необходимости детализировать это уравнение, достаточно упомянуть, что оно в общем является функцией оператора р. Как говорилось ранее, функция преобразования нейрона может быть достаточно хорошо описана нелинейным дифференциальным уравнением восьмого порядка, однако её тоже можно записать как f (p). Беда в том, конечно, что хотя и можно её так записать, в действительности мы её не знаем. Трудность здесь точно такая же, как в заявлении «пусть х есть число жителей в данном городе». Далее мы свободно пользуемся параметром х в наших расчётах, и, по-видимому, можно было бы подсчитать число семей в городе как функцию от х, но рано или поздно нам придётся выяснить, что же стоит за числом х.

В технике управления существуют методы точного определения дифференциального уравнения функции f (p). Прежде всего она устанавливает связь между входной и выходной величинами. Это означает, что мы можем определить f (p) = o / i, где i — входная переменная; о — выходная переменная величина. Когда дело идёт об электрических цепях управления, входная и выходная величины поддаются непосредственному измерению. Более того, если можно построить график зависимости выходной величины от входной во всём диапазоне их изменений, то можно с уверенностью считать наличие зависимости между ними. Функция преобразования и есть уравнение, описывающее такую зависимость. Она может быть очень сложной, но её можно найти, особенно потому, что мы обычно располагаем множеством доступной информации относительно переключателей и цепей, из которых состоит изучаемая система. Знание структуры системы позволяет математикам предсказывать вид требуемого в данном случае уравнения. Найти значение f (p) в типичной кибернетической ситуации может оказаться невозможным. Как мы уже видели, трудно и отчасти, может быть, лишено смысла принимать что-то за входную или за выходную величину в физиологических, социальных и управленческих ситуациях. Может оказаться невозможным выделить, и тем более измерить, интересующие нас переменные. Тогда нам никак не удастся получить зависимость переменных на выходе от переменных на входе. А если структура цепи, как говорилось, представляет собой анастомотик ретикулум, то трудно сформировать какую-либо математическую гипотезу относительно формы, соответствующей данной функции преобразования.

Однако мы должны вернуться к инженеру-автоматчику и его сервомеханизму, как называется его прибор управления. Инженер знает входную, выходную переменные и функцию преобразования для своей системы. Стоящая перед ним задача сводится к следующему: выходной результат системы может не полностью соответствовать тому, который ему нужен. Предположим, например, что при устойчивой входной переменной функция преобразования даёт устойчивую выходную переменную, которая точно соответствует желаемой. Пусть теперь входная переменная начнёт регулярно изменяться — что произойдёт с выходной величиной? Она может следовать за входной, поскольку предполагалось, что выходная величина должна быть постоянной. Хуже того, выходная величина, будучи поданной на вход, может усиливать колебания в системе и дать сильное раскачивание, опасное для следующей системы, выходная величина данной системы для которой является её входной величиной. Что бы ни случилось, во всяком случае, можно измерить текущие изменения значений переменной на выходе и сравнить их с ожидаемыми. Полученные при таком измерении результаты выявят отклонения системы от нормы. Именно такие измеренные величины, которые могут быть несколько видоизменены, подаются обратно с целью регулировки входной величины так, чтобы при существующей функции преобразования была сформирована правильная выходная величина.

Представим себе такой простой цифровой пример: пусть функция преобразования удваивает входную величину. Пусть в данный момент значение на входе равно 3, тогда на входе будет 6, а 6 и есть то, что мы хотим. Представим теперь, что по неизвестной нам заранее причине значение на выходе внезапно стало равным 8. Тогда отклонение на 2 будет воспринято как изменение значения на выходе, а отсюда следует, что значение на входе по той или иной причине по своему эффекту стало равно 4. Цепь обратной связи воспримет как свою входную величину отклонение выходной величины (на 2 единицы) и теперь должна сработать при таком его значении. Если она просто направит обратно отклонение в 2 единицы как поправку на вход в систему, то теперь при его, как мы помним, значении, равном 4, на входе останется только 2. Функция преобразования его удвоит, и новое значение на выходе станет равным 4 вместо 6. Ясно, что цепь обратной связи нуждается в своей собственной функции преобразования, которая снизит первичное отклонение выходной величины с 2 до 1 и заставит первичное отклонение на входе снизиться на это значение. Тогда выходное значение системы возвратится к требуемой цифре б, поскольку входная величина теперь исправлена на 3.

Этот пример хорошо демонстрирует механизм действия отрицательной обратной связи, исправляющей ошибку, но он с дефектом.

Мы заморозили систему, чтобы рассмотреть фактические показатели, а затем позволили ей работать снова на конечном интервале времени, необходимом для срабатывания обратной связи. Однако причиной всех неприятностей является неожиданное изменение входного сигнала, и, вероятнее всего, он изменится снова к моменту проведения корректирующих действий. Тогда то, что произойдёт за время отклонения и введения в систему обратной связи, сложнее, чем просто изменение на обратное значение первичной функции преобразования. Если бы это была единичная операция, то легко было бы видеть, что систематическое изменение входной величины, которое происходит в фазе с временным циклом обратной связи, будет не подавлено, а усилено. Наш механизм обратной связи обнаружит первичное отклонение +2, и снижение входной величины на единицу последует точно в момент, когда на входе будет импульс, приводящий в результате к отклонению на —2. Иначе говоря, на входе останется величина 2, что генерирует 4 скорее, чем 6. Тут начнёт действовать обратная связь, считывающая первое (позитивное) отклонение, и снизит входное значение с 2 до 1. Теперь на выходе останется 2 вместо 6, что ещё хуже.

Из этого следует, что в цепи обратной связи должна быть обеспечена своя собственная функция преобразования, которая может быть записана как F (p), и она должна быть умно реализована, чтобы скорее подавлять, чем усиливать флуктуации на входе. Допустим, что так или иначе это может быть сделано и мы получим тот впечатляющий результат, которого добиваемся — саморегулирующий механизм, в основе действия которого лежит не причина нарушения, а производимый ей эффект. Дело в том, что причиной отклонения может быть или изменение температуры (а в системе не предусмотрено её обнаружение), или нарушение соединения (которое не предполагалось), или отказ в другой системе, генерирующей входную величину для данной системы (о которой система «ничего не знает»). Для нас важно, чтобы управление осуществлялось независимо от причины нарушения.

Чтобы уяснить различие между первичной функцией преобразования f (p) и новой функцией F (p), мы должны обратиться к первичной сети и сети обратной связи, которые управляются этими двумя функциями соответственно. «Сеть» — по-прежнему подходящий для нас термин, поскольку реальные системы значительно сложнее простых из числа здесь рассмотренных, в которых можно разглядеть единичные линии и цепи. «Сеть» на простом русском языке звучит лучше, чем латинское «ретикулум», как упоминалось ранее, поскольку теперь мы создаём систему со специально приспособленными соединениями. К названию ретикулум будем прибегать, ссылаясь на общие и, возможно, специальные случаи внутренних соединений в том контексте, в каком это слово первоначально было введено.

Рисунок № 8.

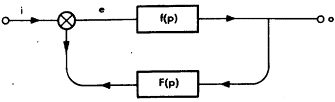
Теперь обратимся к схеме простого сервомеханизма (Рис. № 8) — нам предстоит исследовать характеристики обратной связи на основеих математического описания. Это не означает, что мы будем изучать конкретные дифференциальные уравнения — вся дискуссия ограничится элементарными алгебраическими уравнениями, но это надо преодолеть. На вход системы обратной связи подаётся выходная величина основной системы — о. Выходная величина системы обратной связи есть результат воздействия на величину о функции преобразования системы обратной связи, то есть oF (p). На входе предыдущей системы в результате воздействия обратной связи вместо величины i будет величина е = i + oF (p).

Если это так, то форма функции преобразования первичной системы изменится. Первоначально мы её записали как f (p) = o / i, но теперь это неверно. На входе основной системы (прямоугольник f (p) теперь уже величина не i, а е, представляющая суммарный эффект входной величины i и величины, обусловленной действием обратной связи, oF (p).

Поскольку на входе блока f (p) величина е, а на выходе о, то f (p) = о/е. Чтобы получить функцию преобразования всей системы, мы должны вернуться к основному определению, в котором выходная величина сравнивалась с входной, и записать новую функцию я (р), которая устанавливает правильное соотношение между функциями f (p) и F (p). Конечно, просто записать 0 (р) =o/i. Но чтобы сделать то, что нам нужно, перепишем уравнение для первой системы f (p) и уравнение для е. Тогда получим o (р) = o/i = f (p) / [l-f (p) F (p)].

Из данного уравнения следует несколько выводов. Во-первых, видно, что обратная связь может стать либо положительной, либо отрицательной.

Рассмотрим произведение функций обратной связи первичной цепи и цепи обратной связи, а именно f (p) F (p). Предположим, что система не требует коррекции, то есть функция обратной связи не оказывает никакого влияния. Тогда перемножение функций даст нуль и общая функция преобразования o (p) будет правильно работать как f (p) сама по себе. Если произведение функций будет больше нуля, то знаменатель станет меньше единицы, а общее значение функции больше значения функции преобразования первичной цепи — в итоге получится положительная обратная связь. Если произведение функций станет меньше нуля, то знаменатель станет больше единицы и значение результирующей функции станет меньше значения функции преобразования первичной цепи — получим отрицательную обратную связь. Очевидно, что в одной и той же системе может быть как положительная обратная связь, так и отрицательная, в зависимости от формы переменной, действующей на входе, и сдвига по фазе во взаимодействии этих двух цепей.

Во-вторых, весьма интересен результат действия отрицательной обратной связи. Корректирующая обратная связь по необходимости должна быть отрицательной, если любое отклонение от заданной нормы считается по его абсолютному значению положительным. Тогда уравнение для е должно быть переписано как e = i — oF (p), поскольку нам известно, что абсолютное значение функции преобразования погрешности должно вычитаться из первичного значения входной величины. Тогда уравнение для общей функции преобразования следует переписать в виде o (р) = f (p) / [1 + f (p) F (p)].

Анализируя это уравнение, можно определить, что происходит, если значение функции преобразования первичной цепи становится очень большой величиной. При значении f (p), существенно превышающем единицу, единицей в знаменателе можно пренебречь и сократить числитель и знаменатель на f (p). В таком случае в схеме с обратной связью определяющей станет функция преобразования цепи обратной связи. Формально это можно записать так: если | f (p) |> l, то o (p) ~ = l / F (p).

Результат поразителен. У нас может быть очень слабый сигнал на входе, как это часто случается в биологических и управляющих ситуациях. Мы можем сильно усиливать этот сигнал в первичной цепи, и это часто случается. Тогда можно предположить, что любой «шум» на входе, то есть по смыслу любая неверная информация на входе, станет также сильно усиливаться. Но поскольку в системе в целом преобладает влияние не первичной цепи, не первичной системы, а системы обратной связи, то именно она обеспечит на выходе сигнал, значительно «чище», чем можно было ожидать.

Таким образом, мы оказываемся на пути к достижению желаемого качества системы — её сверхустойчивости. Отрицательная обратная связь во всех случаях корректирует величину на выходе в соответствии с флуктуациями на входе. Неважно, какого сорта шум действует на систему, как он велик по сравнению с входным сигналом, насколько он хаотичен и почему возник. Система стремится подавить его влияние.

Примечание. Результат решения последнего уравнения интересен и важен для понимания сверхустойчивости. Используемая здесь математика проста несмотря на введение уравнений, а аргументация понятна каждому, знакомому со школьной алгеброй. Тем не менее некоторые читатели не понимают, ни как получено уравнение для я (р), ни как исчезло значение е. Поскольку под последним подразумевается «ошибка», его исчезновение особенно примечательно. Поэтому здесь в соответствии с Рис. № 8, осуществим все промежуточные алгебраические выкладки, демонстрирующие доказательства. По определению, f (p) = o / e, (1) e = i + oF (p). (2)

Из (1) следует, что о = ef (p). (3)

Подстановка в (2) даёт i = e — oF (p). (4)

Используя результат (3) и (4), получаем общую функцию преобразования o (р) = o/i = е f (p) / (e — oF (p). (5)

Подставляя значение о согласно (3) в знаменатель (5), получаем o (р) = o/i = ef (p) / (e — ef (p) F (p). (6)

Сократив е в числителе и знаменателе (6), имеем o (р) = o/i = f (p) / (l — f (p) F (p). (7)