Стаффорд Бир:
Мозг Фирмы.
Часть I. Концептуальные компоненты.
Глава 3. Масштабы проблемы

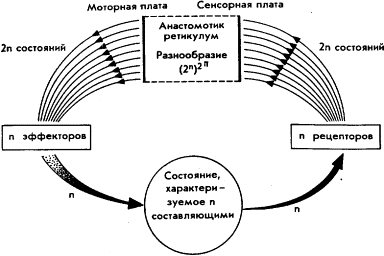
Всякая система управления состоит из трёх основных частей: входного устройства, выходного устройства и сети связи, которая соединяет их. Эта сеть в самом общем случае является анастомотик ретикулум. Теперь попытаемся найти численное выражение, количественно характеризующее такую систему. Многое можно сказать о масштабах проблемы исходя из уже перечисленных первых принципов.

Прежде всего должен быть организован вход, начиная с набора рецепторов, которые передают информацию о некоторых аспектах состояния внешнего мира в эффективно действующие каналы, и заканчивая сенсорным регистратором (или сенсориумом), в котором эта информация собирается. Принципиально такое сенсорное устройство можно встретить везде, как в живых, так и в искусственно созданных системах. Телефония использует различные способы вибрации диафрагмы в телефонной трубке в качестве набора рецепторов, с помощью которых голос направляется во входной канал — телефонный провод. Диафрагма на другом — слуховом — конце трубки принимает колебания, переданные по каналу связи, и работает как сенсорное устройство. Несколько по-другому осуществляется телевидение: передающим каналом в нём служит не провод, а радиоизлучение. Но и здесь сканирующая система телекамеры представляет собой набор рецепторов, передающих элементы изображения; они собираются вместе на внешней поверхности телевизионной трубки, которая представляет собой хороший пример сенсорного регистратора-сенсориума.

Совершенно очевидно, что способности различать детали на каждом конце входного устройства (рецептора и сенсориума) должны быть равными для обеспечения эффективной работы системы. Так, если сенсориум обладает большей возможностью различать детали, чем рецептор, то эта его способность будет потеряна, поскольку приниматься будет лишь часть сигналов, генерируемых передающим устройством. Если же, наоборот, рецептор будет более мощным в смысле различения деталей и эта детальная информация будет передана сенсориуму с худшей разрешающей способностью, то некоторые детали будут просто утрачены. Другое очевидное заключение сводится к тому, что пропускная способность любых каналов, используемых для передачи информации между рецепторами и сенсориумом, должна быть достаточной, чтобы передать её всю. Это особенно ясно, когда передающий канал — механический.

Возьмём, к примеру, в качестве входного устройства системы пишущую машинку. (Её можно рассматривать в качестве самостоятельной системы, поскольку то, что считается системой, определяется исследователем, и он определяет её границы исходя из своих целей.) Клавиши пишущей машинки представляют собой рецепторы с разрешающей способностью, скажем, 92 различных символа. Тогда у нас будет 46 клавиш и устройство, позволяющее работать на двух регистрах. Клавиши сделаны для того, чтобы машинистка могла ввести текст в систему, которая собирает его на сенсориуме — бумаге. Если у нас 46 клавиш, то должно быть 46 рычагов, способных донести металлические символы до бумаги, и устройство для переключения регистра, выступающее в виде своеобразного усилителя, поскольку с его помощью удваивается число символов (сколько бы их ни было), представленное числом клавиш. Важно также, чтобы канал передачи обладал соответствующей ёмкостью не только в смысле способности различать сигналы, но и в смысле скорости действия. Опытная машинистка, пытающаяся использовать старую машинку, столкнётся с тем, что рычаги, несущие знаки, недостаточно быстро сменяются, в результате чего два из них могут сцепиться и помешать друг другу.

Но то, что справедливо в отношении входа, справедливо и в отношении выхода — второго компонента любой системы управления. Возьмём моторную плату, которая передаёт команды набору эффекторов. Здесь мы вновь столкнёмся с тем, что нет смысла располагать большей разрешающей способностью на одном конце, чем на другом. Какими бы ни были наши порывы действовать, но если их нельзя ни передать дальше по имеющимся каналам, ни превратить затем в соответствующие действия, они бесполезны в любом случае. Если кто-то кричит, пытаясь дать полезные советы яхтсмену, испытывающему трудности при входе в гавань, а звуки сносятся ветром, то это бессмысленно — у него нет эффективного канала связи. Опытный музыкант, играющий этюд Шопена на рояле, прекрасно знает, какую клавишу нажимать, поскольку он обладает обычным человеческим телом и располагает достаточной ёмкостью каналов, чтобы преобразовать требуемую ноту в движение мускулов. Но если человек никогда не учился игре на рояле, то он бессилен произвести требуемые действия. Он не обладает эффекторами (выходными преобразователями).

Третья часть системы управления — анастомотик ретикулум, который соединяет сенсоры с моторной платой, о нём нам ещё предстоит поговорить подробнее. А сейчас попытаемся оценить масштаб проблемы, перед которой стоит система управления любой сложной организацией, такой как человек или промышленная фирма в смысле требований к её входным и выходным параметрам. И уж поскольку эти части системы вновь упомянуты, вместе, отметим один любопытный факт. Мы говорили о способности частей системы управления различать детали. На стороне входа необходима пропускная способность, равная числу рецепторов на сенсорной плате; на стороне выхода та же разрешающая способность должна быть на моторной плате с её эффекторами действия. Рассматривая систему управления в целом, мы видим, что необходимые мощности на входе и выходе должны быть равными. Основания для этого всё те же, если мы по-прежнему исходим из того, что критерием является эффективность системы. Обычная ситуация, когда, например, в каналах передачи информации из-за их физических свойств информация искажается, должна рассматриваться по-другому. В таком случае потребуется большее, чем должно было бы быть, количество входных данных, а избыток будет использован для компенсации ухудшения каналов связи. Например, если посыльный, которого мы направляем с письмом, с вероятностью 0,5 будет по дороге убит, то мы обязаны посылать по крайней мере двух человек с письмом одинакового содержания, хотя, конечно, на другом конце необходимо только одно письмо.

В кибернетике число различаемых объектов (или различаемых состояний того же объекта) называется «разнообразием». Тогда, подводя итог вышесказанному, можно считать, что разнообразие на входе должно (по крайней мере) соответствовать разнообразию на выходе для системы в целом, но для входного и выходного устройства оно решается самостоятельно. Это существенно важное следствие закона Эшби о разнообразии систем, которое гласит, что управление может быть обеспечено только в том случае, если разнообразие средств управляющего (в данном случае всей системы управления) по крайней мере не меньше, чем разнообразие управляемой им ситуации. Этот закон, как и любой другой важный закон природы, совершенно очевиден после того, как он открыт. Нетрудно, однако, обнаружить примеры систем управления, поведение которых в значительной степени не соответствует этому закону и, следовательно, неудовлетворительных. Начиная с управления уличным движением и заканчивая национальной экономикой — ошибки очевидны, и, конечно, это одна из ключевых проблем управления промышленным предприятием. Руководители всегда надеются создать простую и дешёвую систему управления, но часто заканчивают потерей крупных денежных сумм на то, чтобы обеспечить с запозданием требуемое разнообразие, которое должно было бы создаваться прежде всего.

Важно определить меру разнообразия промышленного предприятия. Чтобы понять в чём тут дело, мы постепенно подойдём к пониманию того, как растёт разнообразие и каким путём оно может быть воспринято, то есть к тому, что собственно и есть управление. Рассмотрим для начала проблему чтения через её основную составляющую — распознавание букв. Мы хотим получить возможность различать 26 букв английского алфавита, оставляя в стороне такие сложности, как строчные и прописные, тип шрифта, и так далее. Представим тогда себе 26 различных карточек, на каждой из которых напечатана одна буква алфавита, и создадим рецептор, который их рассматривает по отдельности.

Пусть единичный визуальный рецептор представляет собой простое устройство, отличающее светлое от тёмного. Им может быть, например, фотоэлемент, который можно отрегулировать так, чтобы он «чувствовал» границу между светлым и тёмным. Фотоэлемент, таким образом, будет обладать двумя состояниями, которые мы назовём 0 и 1. Если перед таким единичным рецептором окажется карточка с буквой А, то он зарегистрирует меру её серости как определённую смесь чёрного и белого на этой карточке. Он не определит форму, которой для нас соответствует буква А, а определит нечто уникальное в букве А из серии наших карточек. Далее буква В может дать другую смесь белого и чёрного, другую градацию серости. Поскольку мы можем изменять порог чувствительности фотоэлемента, чтобы он регистрировал либо 0, либо 1, то появляется возможность менять порог его чувствительности (по крайней мере теоретически) так, чтобы он отличал букву А от В. Когда мы дойдём до С, то разнообразие нашего фотоэлемента, увы, уже исчерпается, то есть мы уже ничего не можем сделать с последующими буквами от С до Z. Ясно, что одного рецептора недостаточно. Более того, как нам кажется, нужно 26 рецепторов, каждый тщательно отрегулированный на свою букву. Если это так, то мы удовлетворим закон о требуемом разнообразии: число фотоэлементов, присоединённых к входным рецепторам и сенсориуму, станет соответствовать 26 состояниям рассматриваемого нами любого слова.

Однако если у нас есть только один первичный рецептор, то мы можем проделать с ним трюк другого сорта. Можно разделить весь набор карточек с буквами на две части так, чтобы в одной половине оказались более светлые, а в другой тёмные буквы. (При этом предполагается, что можно создать такой шрифт, у каждой буквы которого будет своё особое соотношение чёрного и белого.) Такая их организация позволит относить карточку только к одной из двух групп, поскольку такова возможность рецептора оценивать разнообразие. Но этот элемент будет обследовать все карточки и рассортировывать их на две пачки — на более светлые (которые рецептор принимает за 0) и более тёмные (которые принимаются за 1). Если мы достаточно точно установим границу чувствительности, то в каждой пачке у нас будет по 13 карточек. Рецептор, таким образом, в состоянии считывать все 26 карточек и давать 26 сигналов, один за другим, как серию нулей и единиц и распределять каждую карточку в соответствующую пачку.

Преимущество всего этого в том, что здесь один рецептор с разнообразием два (а именно, 0 или 1) способен уменьшить, в два раза размерность решения проблемы соотнесения любой из 26 букв. Мы, таким образом, получили 13 разнообразных вариантов за счёт двух. Может показаться, что пользы в этом мало, однако это весьма важно. Вообще, двоичный классификатор (рецептор 0 или 1) при эффективном использовании в два раза уменьшает неопределённость, с которой он встретился. Все проблемы, относятся ли они к распознаванию, классификации или к самому решению, — проблемы неопределённости. Если нет неопределённости в отношении промышленной ситуации, то руководителю не нужно принимать решения. Если нет неопределённости в начертании буквы, то мы можем её прочесть. Ситуациями с большей неопределённостью трудно управлять именно потому, что мера их разнообразия и есть мера их неопределённости.

Именно поэтому так важен трюк, который мы только что продемонстрировали. Как бы ни была велика проблема, её разнообразие, в принципе, может быть уменьшено в два раза с помощью одного решающего элемента. Приведём другой пример. Вы ищете кого-либо в танцевальном зале, где танцуют 500 пар. Разнообразие тогда составляет 1000; фактор неопределённости составляет 1:1000, а вероятность правильного решения при случайной выборке равна 0,001. Таков масштаб проблемы. Но если вы знаете, ищете вы мужчину или женщину, то масштаб проблемы сразу уменьшается в два раза.

Вернёмся теперь к проблеме чтения всего алфавита. Мы показали, что 13 более светлых букв могут отличаться от 13 более тёмных букв с помощью одного избирательного рецептора, способного определять среднюю границу их серости. Взяв теперь пачку карточек из 13 букв и второй рецептор, получим возможность отделить 6 одних букв от 7 других, используя такое же устройство — фотоэлемент, порог чувствительности которого соответствовал бы середине между самыми тёмными и самыми светлыми буквами. Конечно, такой же рецептор можно использовать для сортировки и второй пачки букв, когда до них дойдёт очередь. Для сортировки шести (или семи) карточек используем третий рецептор, который сведёт проблему к двум новым половинам (из 3 или 4 карточек). С помощью четвёртого рецептора мы сможем разобраться и с этими пачками, поскольку знаем, что каждая буква уже проверена и является одной из двух. Тогда пятый рецептор различит и эти оставшиеся две буквы. Неопределённость, с которой мы начали — определить любую из 26 букв, исчезла: теперь мы знаем, какая буква какая, и достигнуто это использованием пяти фотоэлементов.

Таким образом, в принципе необходимо только 5 рецепторов, чтобы прочесть буквы английского алфавита, поскольку их достаточно, чтобы различать 2⁵ = 32 буквы, полагая, что у каждой буквы своё соотношение белого с чёрным, своя мера серости, которая уникальна. В общем, n является минимальным числом рецепторов, способных различать 2ⁿ возможностей. Заметьте, что таким образом по мере увеличения числа возможностей получается впечатляющая экономия числа рецепторов. Десять рецепторов могут различать 2¹⁰ = 1024 буквы или чего-то другого. Сорок рецепторов смогут различать 2⁴⁰, что больше миллиона миллионов. Такое число — чистая теория. Мы должны заметить, что на практике такое множество букв (или состояний, или картин нашего мира) не может быть точно различимым. Частично так происходит, поскольку пороги различия их серости становятся слишком близкими друг другу, чтобы использовать практически полезный инструмент их различения, а частично из-за того, что буквы невозможно напечатать с такой аккуратностью. Другими словами, нечёткость их контуров даёт такую меру серости для одной буквы, которая точно соответствует тому, что есть у другой, которую нужно от неё отличить. Так мы подошли к проблеме разнообразия в пропускной способности канала связи как отличающейся от разнообразия на входе.

Мы можем начать обсуждение проблемы снижения разнообразия с другого конца. Сканирующая система телевидения располагает сотнями линий, и сотни разной яркости чёрных и белых точек передаются по каждой линии. В конечном счёте для создания картинки на экране трубки должны использоваться десятки тысяч двоичных рецепторов. Подобно этому в каждом человеческом глазу содержится около миллиона двоичных рецепторов. Неудивительно тогда, что глаз или телевизионная трубка может различать 26 букв алфавита, поскольку, как было показано, для этого достаточно и пяти рецепторов. Из этого вытекает важное заключение: используя значительно большее число рецепторов, чем теоретически необходимо, мы фактически можем разобраться с невероятно большим числом неточностей на входе. Это аналогично нашему примеру о необходимости в двух посыльных для передачи единственного сообщения, хотя на этот раз речь идёт о рецепторах, а не о каналах связи. Благодаря этому люди смотрят телевизионные передачи сравнительно спокойно и, конечно, с пониманием происходящего, когда изображение сильно искажено электрическими помехами. Аналогично и глаз спокойно читает исключительно плохой почерк. Так происходит потому, что у глаза достаточно рецепторов, чтобы различать миллионы букв, а не каких-нибудь 26, но если учесть все возможные алфавиты, включая буквы, написанные от руки, то, вероятно, и нам необходимо большинство этих рецепторов.

Разница между «да» и «нет», между 0 и 1 является элементом решения. Руководители могут уклониться от ответственности, давая двусмысленные или расплывчатые решения: если захотят, могут пробормотать что-то, чтобы отмахнуться, но когда дело доходит до серьёзного, ответ всегда двоичен, фактически руководители всегда используют процесс дихотомической классификации (который был только что нами описан), но используют его совсем не формально. Проблема управления может решаться сотнями возможных способов, и руководитель может отказаться её решать, сказав только, что, по его мнению, решение лежит на том, а не на этом конце шкалы возможных решений. Это звучит весьма неопределённо, но фактически он здесь разделил возможные решения на две группы, которые вполне могут быть неравными, оставляя границу между группами весьма не чёткой. Подчинённые будут разбираться в этих группах в течение некоторого времени, производя действия, которые толкают ситуацию скорее в одном направлении, чем в обратном, пытаясь также избежать зоны перекрытия. Рано или поздно они достигнут такого положения, когда не будут знать, что делать дальше, но представят руководителю значительно суженный круг возможных решений.

Этот процесс будет продолжаться как успешное разделение спектра возможных решений на все новые половины, пока в один прекрасный день руководителю представится возможность сказать «да» или «нет» относительно заключительного предложения. Можно математически показать, что наиболее эффективный путь преодоления последовательности решений такого рода заключается в том, чтобы разделять возможности на две части, причём совершенно не важно, равны ли эти части. Можно, конечно, использовать дополнительный рецептор (что предполагает принятие дополнительного решения) сверх тех, которые минимально необходимы, но это не меняет общего порядка процедуры.

В компьютерах, как всё прекрасно знают, любые сообщения записываются нулями и единицами, в нашем теле нервная клетка либо возбуждена для передачи импульсов, либо нет. В естественных системах, таких как только что упомянутая социальная система управления или такая, как наше живое тело, граница между 0 и 1 вместо того, чтобы быть чётко выраженной, обычно смазана. Поэтому необходимо отличать аналоговый счёт от цифрового (двоичного). Компьютеры, работающие с перфорированных карт или магнитной ленты, формально двоичны, как и обычные счёты. Костяшка счетов передвигается либо в одну, либо в другую сторону, но не занимает неопределённого положения. Но логарифмическая линейка — это аналоговое устройство, поскольку не всегда можно точно сказать, на какой цифре вы остановились, тут есть зона неопределённости. Нервная клетка человека тоже обладает аналоговыми характеристиками, так как нельзя быть полностью уверенным в том, какова граница возникновения импульса. Но она получает двоичный импульс, поскольку электрические импульсы, проходящие по нервам, прибывают группами, интенсивность которых варьируется по частоте их поступления, а не по амплитуде. Так, например, боль становится острее вследствие увеличения числа поступающих по нерву импульсов в единицу времени, а не потому (как думают многие интуитивно), что увеличивается их электрический потенциал. Совершенно также нервная клетка либо посылает импульс, либо нет, но нет вопроса о выдаче ей большого или малого импульса. Преобразование нервной клеткой входящего импульса в выходящий (так сказать, её функция преобразования) — значительно более трудная проблема.

Большинство систем управления, которые интересуют кибернетиков, представляют собой смесь систем аналогового и дискретного счёта. Важность этого утверждения в том, что в любом из этих случаев по-прежнему разнообразие их состояний можно измерять через двоичное решение. Неопределённость границ — в конце концов другого сорта неясность, которая рано или поздно будет решена. Теперь выяснилось, что элементарное решение как выбор между «да» и «нет», между 0 и 1 является исходным в теории управления. Оно называется двоичной единицей, или сокращённо битом. В дальнейшем будем широко пользоваться этим термином, так что не ошибётесь, полагая, что биты — это понятия, которым пользуются только специалисты по вычислительной технике, а для всех остальных они интереса не представляют. Измеряя масштабы проблем, при обсуждении их сложности удобно использовать биты как единицу измерения, поскольку они для этого и предназначены. Если ситуация характеризуется 1024 разнообразными состояниями, то единственное достоинство в знании этого числа заключается в возможности сказать, что нужно принять 10 решений, чтобы рассеять неопределённость, заключённую в этом разнообразии, поскольку 1024 = 2¹⁰. Это просто означает, что для получения одного-единственного ответа мы можем разделять проблему пополам 10 раз. Другими словами, бит является мерой экспоненты в нашей формуле 2ⁿ; он точно равен числу n.

Такова таким образом природа фундаментального механизма, позволяющего нам как жителям этого мира или как руководителям предприятий справляться с огромным разнообразием, встречающимся в жизни. Мы можем распознать или выбрать, или принять решение на основе триллиона вариантов, используя только 40 хорошо продуманных рецепторов или классификаторов. Даже если мы неэффективно разрабатываем свою систему, планируем её процедуры, результат весьма впечатляет. Мы также открыли меру, которую уместно использовать, размышляя о проблемах управления и при разработке инструментов управления. Тогда что же произойдёт с законом о требуемом разнообразии? Ответ таков: мы можем создать генератор разнообразия в механизме управления, подобный тому, которым располагает природа для роста разнообразия как средства преодоления проблем управления.

Пока всё хорошо, но теперь природа берёт свой реванш. Если мы, управляющие, можем создавать очень большие множества из небольшого числа элементов, то, то же может делать и природа. Посмотрите: мы заявляем, что нам необходимо 5 рецепторов для чтения 26 букв латинского алфавита. Представим себе тогда пять лампочек, которые могут зажигаться в любом порядке. (Первая горит, остальные выключены, две горят, три не горят и так далее) Тот факт, что 5 рецепторов могут различать 26 букв, означает, что эти 5 лампочек могут создавать 32 комбинации, и, конечно, если мы хотим представить себе, что означает наше окружение, то должны понимать то, чем оно располагает. Тогда если ваш внешний мир располагает всего 40 лампочками, то из предыдущего мы знаем, что можем встретиться с триллионом разных состояний. Верно, что нам, чтобы разобраться в них, необходимо всего 40 информационных попыток — ситуация совершенно симметричная. Но мир состоит не из сорока лампочек, а из миллиардов вещей и событий.

Если вас фактически интересует n вещей и событий, каждое из которых в данный момент либо «вспыхнуло», либо нет, то такой мир предстаёт перед нами в одном из 2ⁿ возможных состояний n вещей. Поняв, сколь стремительно нарастает такая функция, начинаешь осознавать, что создаётся весьма незавидная перспектива. Но если мы хорошо умеем создавать управляющие механизмы, то такая перспектива нас не очень пугает, поскольку это означает, что необходимо такое число рецепторов, сколько насчитывается событий или вещей. Эти n рецепторов создадут 2ⁿ разнообразий на сенсориуме. Моторная система сведёт 2ⁿ состояний к возможным конкретным действиям. Мы, таким образом, сохранили требуемое разнообразие. Однако вспомним приведённый ранее аргумент: если вещей или событий больше, чем рецепторов, которые их распознают и сообщают о них системе управления, то мы не можем все их определить. И здесь мы вновь сталкиваемся с законом о требуемом разнообразии. В любой данный момент нас будет касаться лишь то, о чём мы знаем, и не больше, а его разнообразие равно n. Разнообразие n создаёт 2ⁿ состояний, но наши процедуры выбора позволяют нам с этим справиться с помощью n процедур распознавания или n процедур выбора, то есть именно с тем их числом, которым мы располагали по определению. Но беда начинается, когда необходимо предпринимать какие-то действия.

Мы уже упоминали, что входные и выходные устройства симметричны и подчиняются закону о требуемом разнообразии. Это требование в равной мере распространяется как на входы, так и на выходы устройства. Реальная проблема управления, которую необходимо решать мозгу, сводится к проблеме сопоставления положения на входе с положением на выходе, с помощью анастомотик ретикулума. Если разнообразие возникающей перед нами ситуации равно n, то разнообразие на сенсориуме равно 2ⁿ. А если по закону о требуемом разнообразии необходимое число действий составляет n, то разнообразие на моторной плате будет также 2ⁿ. Каково же тогда разнообразие внутри сети, соединяющей сенсорную и моторную платы? Оно равно числу возможных комбинаций 2ⁿ из 2ⁿ, то есть (2ⁿ)^2.n. Это утверждение проясняет Рис. № 9.

Рисунок № 9.

Если до этого мы рассуждали спокойно, то теперь пришло время поднять настоящую тревогу. Дело в том, что числа такого вида немыслимо велики. Следует понимать, как это получается. Уже объяснялось, почему n разнообразий создают 2ⁿ состояний на сенсориуме. Объяснение достигалось по мере демонстрации того, как с целью поиска решения разнообразие разделялось пополам. Каждый доступный нам вариант выбора удваивает разнообразие. Начав с единственной возможности, мы позволяем создавать альтернативу: 0 или 1. При повторении этой процедуры 0 создаёт снова либо 0, либо 1, а единица — тоже 0 или 1 и так далее.

Рассмотрим чёрный ящик всего с двумя входными и двумя выходными величинами. На обеих его сторонах — сенсорной и моторной — при n=2 генерируется 2ⁿ = 2² = 4 состояния: 00, 01, 10, 11. Сколько же будет соединений? Ответ таков — моторное разнообразие [4] увеличивает мощность сенсорного разнообразия [4] в 4⁴ раза, а именно в 256 раз.

Как может показаться, в это трудно поверить, поскольку мы начали всего с двух двоичных входных и двух двоичных выходных величин. Но рассмотрим одно из четырёх возможных выходных состояний, скажем 00. Оно может быть, а может и не быть зарегистрировано как одно из четырёх выходных состояний. Обозначим одно из несостоявшихся соединений 0, а действующее 1. Следующая таблица демонстрирует возможные состояния системы:

16 различных состояний

В этой системе вполне различимы 16 состояний, хотя рассматривалось лишь одно выходное состояние. Однако мы располагаем четырьмя выходными состояниями, в равной мере способными вызывать шестнадцать других состояний внутри системы. Общее взаимодействие входных и выходных состояний даёт общее разнообразие системы 16 × 16 = 256. Как говорилось, используемая здесь формула 4⁴, а поскольку каждая из этих четвёрок есть 2ⁿ, где n = 2, то ясно, почему мы ранее записывали наш результат как (2n)²ⁿ

Почему же нам пришлось так подробно в этом разбираться и почему мы заговорили об этом с тревогой? Ответ состоит в том, что любая система управления генерирует столь большое разнообразие, используя этот механизм, что буквально нет никакой возможности его проанализировать и, следовательно, нет способа (как кажется). соединения анастомотик ретикулума. «Буквально» здесь сказано точно — задача кажется научно неразрешимой, не говоря уже о её бесконечно большой размерности. Если это так, то не следует и надеяться, что в один прекрасный день появятся достаточно мощные и быстродействующие компьютеры, позволяющие решать задачи, которые решить нельзя. Факты надо признавать, они таковы.

Рассмотрим наименьший «мозг», которым стоило бы располагать, чтобы справиться с управлением сложной ситуацией в реальной жизни любой фирмы. Окружающая её среда характеризуется числом разнообразия её состояний, не так ли? Если представить себя или нашу фирму в окружающей среде с разнообразием, равным n = 300, то это, конечно, не так уж и много. Такая оценка весьма консервативна. На многих фирмах больше 300 работающих, более 300 станков, более 300 наименований выпускаемой продукции, более 300 клиентов. Для обстановки с разнообразием всего в 300 разнообразие на сенсорной и моторной платах составит 2³⁰⁰. Анастомотик ретикулум, необходимый для соединения этих плат должен обладать разнообразием (2ⁿ)²ⁿ = (2³⁰⁰)²³⁰⁰. Измеряя его в битах (поскольку это самая естественная мера для использования в случаях принятия решения), получаем 300 × 2³⁰⁰ бит, что примерно равно 3 × 10⁹² бит. Такова мера неопределённости в выбранной нами ситуации на фирме, которой не более 300 входных и 300 выходных величин, каждая из которых находится всего в двух состояниях.

Следующий довод, которому мы обязаны Бремерманну, вытекает из физики. Как следует из квантовой механики, есть нижний предел точности, с которой может быть измерена энергия. Это означает наличие постоянной и предельной степени неопределённости материи. Согласно принципу Гейзенберга любая попытка улучшить точность измерения приводит к тому, что погоня за точностью изменяет состояние вещества. Количества здесь малы, но они сильно сказываются на свойствах вещества. Бремерманн приложил этот принцип к 1 г вещества в 1 с и показал, что нижний предел точности измерения материи определяет верхний предел её информационных возможностей. Ниже этого предела нули будут приниматься за единицы и счёт станет произвольным. В течение 1 с, пишет он, 1 г типичного вещества не сможет справиться более чем с 2 × 10⁴⁷ битами информации. Конечно, никто не использовал грамм вещества для передачи столь огромного количества данных — микроминиатюризации ещё далеко до этого. Как он утверждает, даже в конце технологического прогресса нельзя будет, используя 1 г вещества, передать более 2 × 10⁴⁷ бит информации в 1 с, поскольку они начнут искажаться согласно принципу неопределённости Гейзенберга. Так Бремерманн приложил закон о требуемом разнообразии к самой материи.

Такое число выглядит огромным, и действительно мы приступаем к определению мощности растущего с огромной скоростью числа 2ⁿ, где n представляет собой 10 с 47 нулями. Более того, мы можем построить компьютер массой более 1 г и использовать его дольше чем 1 с. Но даже люди, привыкшие иметь дело с экспоненциальными процессами, могут изумиться следующему доводу. Предположим, мы используем всю массу нашей планеты Земля для постройки компьютера и заставим его работать в течение всей её истории. Каким разнообразием будет располагать такая фантастическая машина? Что же, заявляет Бремерманн, в году, примерно, 3 × 10⁷ секунд, возраст Земли примерно 10⁹ лет. Её масса около 6 × 10²⁷ тонн. Тогда такой сделанный из всей Земли компьютер за всю историю нашей планеты обработает (2 × 10⁴⁷) (3 × 10⁷) (10⁹) (6 × 10²⁷) бит. А это составит около 10⁹² бит.

Теперь ясно, почему я выбрал разнообразие n = 300 для примера о мозге фирмы. За несколько абзацев до этого было показано, что ретикулярное разнообразие, которое может быть генерировано таким умом, при весьма консервативной оценке разнообразия такой фирмы составляет 3 × 10⁹² бит. Выяснилось также, что компьютер с массой нашей планеты за всё время существования Земли при идеальном его состоянии и техническом совершенстве необходим для расчёта состояний совсем небольшой фирмы.

Состояние фирменной среды, как и состояние всего человеческого организма, располагает разнообразием, значительно превышающим 300. Даже при самой ориентировочной оценке (исходя из того, что разнообразие на моторной плате должно быть равным на сенсорной) разнообразие живого мозга составит примерно (2¹⁰⁶)²¹⁰⁷, что с полным основанием считается самым большим числом среди серьёзно обоснованных чисел. Если мы хотим действительно разобраться с разнообразием состояний фирмы, то, конечно, у нас нет никаких оснований полагать, что мозг фирмы нуждается в возможности справляться с разнообразием, меньшим, чем это. Мозг Фирмы, как и мозг человека, потенциально может быть в стольких состояниях, что их никогда не удастся проанализировать или исследовать с учётом всех факторов — их немыслимо большое число. Информация должна тогда выдаваться постоянно миллиардами битов и серьёзно контролироваться. Здесь уместно отметить и особо подчеркнуть, что не может и возникать вопроса о нахождении абсолютного оптимума поведения как для человека, так и для фирмы, поскольку нельзя проверить все альтернативы. Из законов природы следует, что это невозможно в принципе.

Отсюда сам по себе анастомотик ретикулум бесполезен. Нужно что-то предпринимать, чтобы управлять всей системой. Должен быть представлен рост разнообразия, его потенциал должен быть уменьшен и становиться всё меньше и меньше, хотя нам неизвестен лучший способ его уменьшения. Нет даже разумного пути фиксирования и поиска информации в системе такого масштаба, не говоря уже о её обработке на компьютере. Гейнц фон Форестер предложил графическую иллюстрацию проблемы подобного «запоминания». Он подсчитал размер таблицы, которая получится, если перемножить все возможные цифры (всего только) до десяти на все другие возможные их комбинации (всего только до десяти). Он предложил также опубликовать результат в справочнике с размером страницы 21 × 28 см на бумаге нормальной толщины. Получится книга толщиной 10¹⁵ см. И снова не математику трудно привыкнуть к такого вида экспоненте. Книжная полка, на которую можно было бы поставить такой справочник, была бы в 100 раз длиннее расстояния от Земли до Солнца. Как утверждает фон Форестер, библиотекарь, который бы бегал вдоль этой полки со скоростью света тратил бы полдня, чтобы достать нужный том.

Полное управление растущим разнообразием совершенно невозможно для человеческого ума или мозга фирмы. Однако как человек, так и фирма фактически работают. Для этого они уменьшают, они должны уменьшать разнообразие их бесчисленных состояний. Для этого мало веры в электронный компьютер. Вопрос в том, как такие системы спокойно и эффективно справляются с подобной задачей? Ответ таков: путём организации.