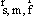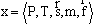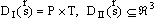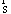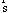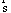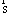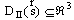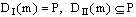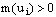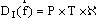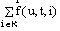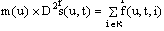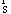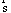Курт Хюбнер:
Критика научного разума.
Часть II. Теория истории науки и исторических наук.
Глава 12. Критический анализ теории историко-научных процессов и научного прогресса Снида-Штегмюллера

В центре концепции, разработанной Снидом и Штегмюллером, стоит идея о том, что понятие научной теории может быть выражено средствами математики, путём введения теоретико-множественного предиката, специфического для данной теории ¹⁹².

Примером может служить классическая механика частицы (КМЧ). Можно определить это понятие следующим образом:

КМЧ [x] существуют множества P и T, функции:

Такие, что:

(1)

Это означает: x есть структура, составленная: из P, T и так далее.

(2)

P — конечное непустое множество.

(3)

T — интервал действительных чисел.

(4)

Где D_I — область определения:

«декартово произведение» (иначе: в области определения:

Частица всегда скоординирована с моментом времени); D_II — ранг:

множество образов, на котором отображена данной функцией область определения:

множество троек чисел;

Означает, что ранг (множество векторов положения) есть подмножество множества троек действительных чисел, поскольку каждый вектор положения частицы определяется тремя действительными числами — её координатами.

(5)

Где

Для всех u P («u P» означает, что u есть элемент множества P).

(6)

Где — множество натуральных чисел, на котором отображается число сил, действующих на частицу;

;

Для всех u P и t T,

Абсолютно конвергентна, то есть сумма абсолютных значений имеет предел.

(7)

Для всех u P и t T,

Где D ² — вторая производная:

Это хорошо известное уравнение: масса ускорение = сила.

По Сниду и Штегмюллеру, это чисто теоретико-множественное определение позволяет сделать эмпирическое утверждение: данная структура имеет некоторое применение a к реальным системам. Например, в виде такой структуры можно представить солнечную систему. Такого рода эмпирические утверждения могут выражаться следующим образом: a имеет структуру, определяемую специальной теорией, сокращённо: a имеет s, где под s понимается фундаментальный закон данной теории (например, КМЧ).

Затем Снид и Штегмюллер определяют понятие «теоретической величины» как величины, полученной при помощи теоретически зависимого измерения. Это значит, что определение величины зависит от предшествующего успешного применения именно тех теорий, в которых эта величина фигурирует. Например, сила и масса — теоретические величины в КМЧ, а положение частицы и время — не являются таковыми, поскольку они могут быть измерены немеханическим способом, скажем, оптическим.

Всякое применение теории a называется моделью S и отличается от возможной (потенциальной) частной модели КМЧ. Например, кинематика частицы (КЧ) — возможная частная модель КМЧ. В соответствии с предыдущим определением:

КЧ [x] существуют множества P, T и функция:

Удовлетворяющая условиям 1–4. Здесь уже не фигурируют масса и сила (то же самое относится к пункту 1, где также фигурировали эти функции). Таким образом, КМЧ предстаёт как «теоретическое расширение» КЧ. Тогда вместо того, чтобы говорить: «a имеет S», можно сказать иначе:

(1) a — возможная частная модель S, и существует теоретическое расширение, обозначаемое x, являющееся моделью S. Это так называемая «примитивная форма Рамсея, выражающая эмпирическое содержание теории».

Но зачем нужна усложнённая формулировка [1] вместо более простой «a есть S»? Снид и Штегмюллер объясняют это так: чтобы проверить «a есть S», необходимо определить значения некоторых теоретических величин. Но по определению для этого нужны успешные применения теории, обладающей структурой S. А чтобы проверить эти применения, надо предположить другие, более ранние применения, и так далее. В результате получается регресс в бесконечность или логический круг. Чтобы избежать этого и выявить эмпирическую истинность [1], утверждают Снид и Штегмюллер, достаточно знать, удовлетворяют ли этой формулировке те величины, которые фигурируют в a. Например, в рамках КЧ и/или КМЧ подтверждение [1] должно основываться на доказательстве той гипотезы, что для некоторых частиц интервал времени и вектор их положения соответствуют друг другу. В таком случае возможно такое теоретическое расширение, которое является моделью КМЧ, другими словами, теоретические функции КМЧ могут быть применены к такой системе a, которая станет возможной частной моделью КМЧ. Таким образом, по сравнению с выражением «a есть S» (1) представляет собой более слабое эмпирическое утверждение, то есть утверждение о лишь возможном, а не об актуальном применении теоретически зависимых величин.

12.1. Критические замечания об определении теоретических величин в концепции Снида-Штегмюллера

Здесь уже напрашиваются некоторые возражения, в особенности против того определения, которое Снид и Штегмюллер дают теоретическим величинам. Почему в это определение должно входить успешное применение теории, от которой эти величины зависят? Не указывает ли на сомнительность такого вхождения тот вывод, к которому приходят авторы концепции — о том, что пространство и время не являются теоретически зависимыми величинами? Как показывают многочисленные примеры, частично приведённые в предшествующих главах, нет таких понятий пространства и времени, которые не зависели бы от сложной системы теоретических предпосылок.

В самом деле, чтобы утверждать истинность «a есть S», нужно проделать специальные измерения, но это возможно только в том случае, когда значимость теорий, необходимых для таких измерений, хотя бы частично предполагалась априорно (и это также уже было показано на примерах). Большего мы не вправе требовать, не рискуя впасть в бесконечный регресс или оказаться в логическом круге; но в действительности и не нужно требовать большего. Даже утверждение «a есть возможная частная модель S», если оно принадлежит эмпирическому содержанию теории, требует определённых измерений. Но тогда, если принять концепцию Снида-Штегмюллера, может ли формулировка эмпирического содержания теории [1] избегнуть тех затруднений, с какими связано выражение «a есть S?» И, наконец, является ли [1] действительно адекватным определением эмпирического содержания теории?

Можно ли с определённостью утверждать, что этому выражению нельзя приписывать значение «a есть возможная частная модель», то есть что данное выражение интерпретировано априорно? В таком случае эмпирическое содержание теории состояло бы в таких, например, высказываниях как «Планетарная система, априорно интерпретируемая в классической механике, характеризуется такими-то и такими-то конкретными движениями, массами и силами», и так далее.

12.2. Критика различия, которое Снид и Штегмюллер проводят между «ядром» и «расширением ядра» теории

Проследим дальше за развитием концепции Снида-Штегмюллера. Итак, у каждой теории есть «подразумеваемые применения» (например, у классической физики — солнечная система, приливы, маятники, и так далее). Для всех этих применений существуют некоторые «ограничения». Так одному и тому же объекту в различных применениях приписываются одинаковые функциональные значения (например, масса Земли считается одной и той же и в рамках солнечной системы, и в рамках какой-либо подсистемы последней). В рамках некоторых применений имеют место «специальные законы», определяющие собой «специализации структуры S» (например, на основании КМЧ формулируются законы гравитации, Гука и многие другие).

С учётом всего этого согласно Сниду и Штегмюллеру получаем усложнённую формулировку Рамсея:

(II). Имеется теоретическое расширение множества физических систем до моделей математической структуры S, такое, что теоретические функции, фигурирующие в этом расширении, удовлетворяют классу предварительно установленных ограничений, и, кроме того, такое, что некоторые собственные подмножества m расширимы до моделей некоторых более узких (специализированных) формулировок структуры S.

Тем самым «ядро» C теории отличается от «расширенного ядра» E. В состав «ядра» C входят: 1) множество возможных моделей (то есть математическая структура теории); 2) множество возможных частных моделей; 3) ограничивающая функция (посредством которой возможные модели связываются с возможными частными моделями); 4) множество моделей; 5) множество ограничений. Если к этим пяти составляющим «ядра» добавить «специальные законы» (здесь мы не будем на этом останавливаться), то получим «расширенное ядро» E.

Главная идея концепции Снида-Штегмюллера в том, что «ядро» C остаётся постоянным в ходе историко-научного процесса, а «расширенное ядро» E изменяется. Таким образом, (II) — эмпирическое утверждение, которое может изменяться с течением времени. «Ядро» — это как бы априорный структурный элемент теории; поскольку он не подвержен изменениям, то и нет надобности в какой-то особой стратегии по его «иммунизации».

Здесь мы вынуждены задать критический вопрос: не является ли демаркация C и E произвольной? По какому критерию эта демаркация может быть объективно или необходимым образом проведена? А если такого критерия нет, то нет и оснований, по которым можно было бы судить, что освящено эмпирией и что нет. Можно согласиться с тем, что определение теории в терминах теории множеств позволяет так «вышелушить» теоретическое «ядро», что оно становится, благодаря формализму, вполне обозримым.

Но необходимо и разумное основание, по которому граница между «ядром» и его «расширением» пролегает так, а не иначе. Скажем, чтобы отнести второй закон классической механики — «сила = масса х ускорение» — к «ядру» и признать его априорную значимость, нужны какие-то исследования, полностью отличные от теоретико-множественных. Штегмюллер и сам признаёт, что измерение величин, определяемых этим законом, уже предполагает наличие этого закона. Кроме того, неверно, что «ядро» теории не требует никакой «иммунизации». Как мы уже видели в предыдущих главах, все априорные элементы теории подвержены исторической эрозии; но именно по этой причине они защищаются своими сторонниками всегда по-разному (иногда — путём привлечения к защите других априорных принципов, иногда — демонстрацией того, что они в состоянии служить прочным каркасом, охватывающим мир опыта и придающим ему осмысленность и плодотворность).

12.3. Критические замечания о «динамике теорий» Снида-Штегмюллера

Теперь мы подошли к определению теории, для которого вводится множество физических систем J, репрезентирующих «подразумеваемые применения» расширенного ядра E. Обозначим класс возможных подразумеваемых применений E как A [E]. Тогда нашим определением будет предложение:

X — физическая теория, если и только если X = <C, J&rt. Следуя Сниду и Штегмюллеру, мы теперь можем получить определение эмпирического содержания теории теоретико-множественным образом. Вместо (II) запишем:

(III). J есть элемент A [E]. [поскольку в (II) — не что иное, как множество J подразумеваемых применений в конкретный момент времени, а E — более точная формулировка S в (II)].

И наконец, мы получим как семантическое, так и прагматическое определение того, что значит «располагать теорией (в момент t)».

Семантическое определение: P располагает теорией T в момент t, если P знает, что [1] J есть элемент A [E]; (2) E — наиболее точная из известных формулировок «расширенного ядра», к которому применимо J; (3) J — максимальное множество, относящееся к применению E. Прагматическое определение:

P располагает теорией T в момент t, если [1] T — теория, которой располагает P, в семантическом смысле; (2) другой субъект P₀ (например, автор теории) устанавливает подразумеваемые применения T при помощи парадигматического множества примеров J₀; (3) J₀ — подмножество множества J, отобранного P в момент t; (4) P убеждён, что существует более точное E’ по отношению к E, такое, что J является элементом также и A (E’); (5) P убеждён, что существует расширение J, такое, что оно является также элементом E’.

Пункт [4] прагматического определения может быть назван «теоретической верой в прогресс науки», а пункт [5] — «эмпирической верой в прогресс науки».

Теперь мы имеем средства для того, чтобы решить главный вопрос: построить теорию историко-научного процесса, или, как выражаются Снид и Штегмюллер, теорию «динамики научных теорий».

Тот исторический факт, что разные исследователи часто пользуются одной и той же теорией, хотя связывают с ней различные гипотезы, можно выразить так, что эти исследователи имеют разные мнения, касающиеся расширенного ядра E или множества подразумеваемых применений J, но в то же время прочно привязаны к одному и тому же парадигматическому множеству J₀.

Тот исторический факт, что теории часто опровергаются [здесь это означает фальсификацию (II) и/или (III)], но при этом не отбрасываются, получает выражение в том, что опровергается лишь «расширение ядра», а само «ядро» остаётся незатронутым и потому не может быть «низложено». Пример, который приводит Штегмюллер: если свет состоит не из корпускул, то это не означает, что опровергнута механика частиц, а только то, что один элемент из множества подразумеваемых применений, относящийся к расширению «ядра» E, исключён из него.

Можно теперь сказать, что нормальное развитие науки происходит тогда, когда расширяются E и J, а революционное развитие, когда возникает новое «ядро» C ¹⁹³. Тем самым объясняется ещё один исторический факт: революционное развитие никогда не начинается с опровержения «ядра» какой-либо теории, поскольку такие фальсификации практически невозможны. Несмотря на неудачи, которые могут преследовать исследователей в попытках расширить «ядро» теории, оно будет оставаться в употреблении до тех пор, пока не будет создано другое, лучшее «ядро». Если какая-то вещь крайне необходима, то лучше её иметь даже в неудовлетворительном состоянии, чем не иметь её вовсе. Кроме того, провал каких-либо попыток расширить «ядро» совсем не означает, что такие попытки вообще безнадёжны.

Что касается Штегмюллера, то он особенно старается создать впечатление, будто теоретико-множественное определение теории является наиболее важным условием объяснения этих фундаментальных историко-научных фактов, и более того, будто эти факты вообще не могли бы быть объяснены без такого определения. Он подчёркивает, что, если рассматривать теорию не теоретико-множественным образом, а как-то иначе, например, как класс предложений, которому (в целом) могут быть приписаны значения «истинно» и «ложно», то неизменность «ядра», которое, так сказать, оказывается «по ту сторону истины и лжи», не могла бы найти объяснение; история науки превратилась бы в иррациональную загадку.

Как мы уже отмечали, теоретико-множественное представление теории действительно имеет то преимущество, что априорная структура «ядра» теории с помощью формальных методов становится особенно прозрачной. Но это никак не отменяет вопрос о том, что именно должно входить в «ядро» теории, что можно называть априорным элементом последней, а что нельзя, каковы критерии, по которым принимаются такого рода решения, что вообще следует понимать под «a priori» в данном контексте. Такие решения могут быть приняты только путём проверки конкретных обосновывающих предложений — могут ли они сами быть обоснованы эмпирически или внеэмпирически — и в этот процесс включается весь системный комплекс, в котором фигурируют эти предложения.

Никакой формализм, в том числе и теоретико-множественный, не избавляет от необходимости содержательного исследования. Сама формальная презентация может состояться только в конце или на заключительных стадиях разработки теории. Для этого теория уже должна наличествовать как достаточно полный класс предложений. Но так никогда не бывает в начале или на ранних стадиях развития теории, то есть когда граничная линия C и E, разделяющая a priori и a posteriori, проводится впервые, когда аксиоматические, функциональные, оправдательные и нормативные основоположения обретают априорное обоснование, тем самым отделяясь от эмпирически данного, что становится очевидным лишь в рамках, создаваемых этими же основоположениями.

Теоретико-множественное представление теорий прячет проблематичность оснований этих теорий за ширмой формальных преимуществ и тем самым камуфлирует историческую обусловленность теоретических конструкций. Штегмюллер прибегает к чисто психологическому объяснению постоянной приверженности «ядру» тех исследователей, которых не смущают многочисленные неудачные попытки расширения этого «ядра», — объяснение сродни тому, что лучше иметь что-нибудь, хоть плохонькое, чем не иметь ничего. Анализ, который проводится им на основе теоретико-множественного представления теории, не позволяет увидеть в этой приверженности исторический, а не психологический феномен; при этом теряется из виду объективная обоснованность этой приверженности конкретной исторической ситуацией — то, что было проиллюстрировано нами рядом примеров, приведённых в предыдущих главах, и представлено в общей форме как теория исторически обусловленных системных ансамблей.

И, наконец, мы видим, что теоретико-множественный анализ не может объяснить, почему наступают революционные преобразования, почему вдруг учёные создают новое «ядро». Штегмюллер не проходит мимо этого вопроса, но то, что ему удаётся сказать, а именно, что революционные изменения происходят тогда, когда старая теория оказывается сводимой к новой, когда новая теория даёт по меньшей мере не худшее объяснение фактам, чем старая и так далее, никак не связано с теоретико-множественным анализом; это просто исторические констатации, которые, как было показано в предшествующих главах, к тому же и неверны. Однако, если рассматривать процессы научных изменений не только в рамках теоретико-множественного анализа, но и дополнять его исторической теорией научного развития, очерк которой представлен здесь, то тогда только и можно понять, почему действительный ход истории науки не соответствует этим констатациям, но тем не менее не является ни загадочным, ни иррациональным.

Концепцию Снида-Штегмюллера в целом можно считать небесполезным инструментом анализа уже сложившихся теорий, хотя она в ряде аспектов имеет спорный характер. Но никакая «динамика теорий», если под этим понимать метатеорию, объясняющую истоки, основание, выбор и историческое развитие научных теорий, из этой концепции выведена быть не может; поэтому такое наименование следует признать неадекватным и порождающим недоразумения.