Курт Хюбнер:
Критика научного разума.
Часть I. ('')еория естественных наук.
Глава 5. Критика аисторизма теорий науки Поппера и Карнапа на примере «Astronomia Nova» Кеплера

Теоретические концепции Кеплера, представленные им в его «Новой астрономии», если рассматривать их под интересующим нас углом зрения, возникли в результате попыток определить орбиту Марса. После многолетних напряжённых трудов Кеплер, наконец, признал, что его прежние подходы к этой проблеме были обречены на неудачу. Этот вывод был сделан после того, как выяснилось, что между значениями, вычисленными в соответствии с его гипотезами, и значениями, полученными в наблюдениях Тихо Браге, имелось расхождения в 8’. Кеплер писал: «Нам же, благодаря милосердию Божию, дан в лице Тихо Браге такой добросовестный наблюдатель, что в его наблюдениях ошибка в 8’, характерная для птолемеева вычисления, попадается лишь для того, чтобы мы с благодарностью оценили эту милость и воспользовались ей. Наконец, это затруднение даёт нам возможность найти истинный вид небесных движений…, установив причины, по каким сделанные предложения были некорректны… Таким образом, эти 8’ указали путь к обновлению всей астрономии, они явились материалом для большей части данной работы» ⁴³.

Такое утверждение никого не удивило бы в настоящее время, разве что своей страстностью. Говорят, что с него берёт начало всё современное естествознание, ибо решающую роль Кеплер отводил данным наблюдения. В принципе это верно, однако, не следует при этом забывать, что беззаботность, с какой прежде обращались с данными наблюдения, то равнодушие, с каким воспринималось даже большее расхождение с ними, чем те 8’, из-за которых Кеплер решился отвергнуть гипотезы о характере марсианской орбиты — почему он и называл их hypothesis vicaria, то есть временными или рабочими гипотезами — никак не могут быть отнесены на счёт низкого уровня науки или личной несостоятельности учёных. В действительности, подобное отношение было тесно связано с теоретическими воззрениями, господствовавшими со времён Птолемея.

Лежащая в основе этих воззрений формула, так называемая аксиома Платона, гласившая, что небесные тела движутся по кругам с постоянной угловой скоростью, отталкивалась от метафизики, согласно которой земной и небесный порядок вещей принципиально различны как несовершенное и совершенное, как низшее и высшее. Эта идущая от Античности теория была отчётливо ориентирована на «спасение явлений» (svzein ta fainomena); поэтому метафизика служила ей средством, при помощи которого вносился порядок в хаос явлений. Когда же это не вполне удавалось, под рукой всегда было объяснение. Разве можно слепо доверять чувствам? И в особенности недопустимо это по отношению к объектам, столь возвышенным и удалённым, как небесные тела. Ощущения могли быть более или менее достоверными, когда они доставлялись вещами подлунного мира, но на их основании нельзя было с уверенностью судить о движениях небесных тел.

Мы были бы слишком наивны, если бы усмотрели в решительном отказе Кеплера от этого, идущего с древних времён, отношения к данным наблюдения свидетельство победы разума и науки в их современном понимании. На самом деле Кеплер только показал, что он руководствуется иными метафизическими идеями, чем его оппоненты. За его приведёнными выше словами стояли фундаментальные теолого-гуманистические тезисы Коперника: Творение по своей структуре доступно человеческому познанию и, следовательно, дух не может противоречить восприятиям; нет непреодолимых различий между вышним и подлунным мирами, а Земля — одно из тел вселенского хоровода; Вселенная устроена по принципу простоты и так далее ⁴⁴.

Но система Коперника со всеми её теолого-гуманистическими предпосылками в духе Ренессанса на самом деле была даже менее обоснована, чем современная ей птолемеевская система. И, как уже отмечалось, чтобы поддержать эту систему, нужно было прибегать к тем же средствам, какие использовались аристотелианцами, то есть выдвигать теологические аргументы против теологических и метафизические аргументы против метафизических. Новая система не имела неоспоримого и единого основания, которое позволило бы судить о её истинности, тем более, что само вращение Земли оставалось неразрешимой загадкой до тех пор, пока сформулированный Ньютоном принцип инерции не объяснил, почему живущие на Земле люди не ощущают этого вращения ⁴⁵.

Решение Кеплера последовать за Коперником, а значит, признать ощущения и данные наблюдений высшей инстанцией, прежде всего было спонтанным актом, а не выводом из рациональных (как бы мы их ни понимали) рассуждений. Следовательно, идеи Кеплера вырастают из культурного контекста, уже готового к тому, чтобы отвергнуть систему Птолемея.

5.1. Теоретико-научный анализ «Новой астрономии» Кеплера

Когда первоначальные попытки Кеплера вычислить орбиту Марса потерпели неудачу, это натолкнуло его на мысль заняться вычислениями орбиты Земли ⁴⁶.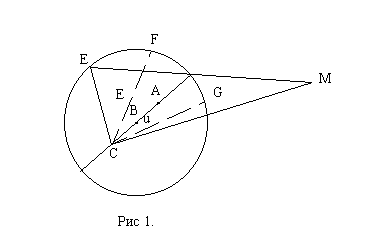

С этой целью, используя теорию Тихо Браге, он вычислил гелиоцентрическую позицию Марса (точка М на рис. 1) и Земли (точка Е) в данный момент времени Т. Углы E и m, образованные соответствующими радиус-векторами и диаметром, на котором расположен сегмент АС, дают представление о том, как была определена эта позиция. Следует только напомнить, что на рис. 1 орбитальные отношения изображены не так, как это было у Тихо Браге, а так, как они были впервые вычислены Кеплером с помощью данных Тихо.

Очевидно, гелиоцентричность здесь — это отнесённость к точке С; но, как было известно уже Тихо Браге, эта точка не соответствует ни Солнцу (точка А на 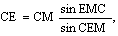рис. 1), ни, как могло бы казаться, центру орбиты Земли (точка В), хотя последнее стало известно позднее. Связав положение Марса с положением Земли (геоцентрическая долгота), Кеплер смог вычислить параллакс ЕМС и угол СЕМ ⁴⁷. Отсюда можно было получить относительное расстояние Земли от точки С (по закону синусов) из уравнения:

Где СМ = 100,000. Затем Кеплер выбрал другой момент Т’, когда Марс опять находился в том же положении, проделав полное обращение по своей орбите, а Земля, учитывая её собственное движение, находилась в другом положении (точка F на рис. 1). Применяя тот же метод, Кеплер вновь вычислил расстояние от Земли до точки C (CF). Наконец, он выбрал третий момент Т» (а затем и четвёртый, который мы здесь опустим); соответственно, он получил третье положение Земли (точка G) и расстояние СG. Из этого он заключил, что С не может быть, как предполагалось, центром окружности, на которой лежали бы все три вычисленные положения Земли. Более вероятно, что эта точка является точкой экванта (punctum aequans), то есть точкой, вокруг которой Земля вращается с постоянной угловой скоростью, поскольку за время перемещения Земли из одной вычисленной точки в другую проходит полный марсианский год, а углы, образованные CE и CF, CF и CG, были равны.

Далее Кеплер собирался вычислить расстояния от точки экванта C и точки Солнца А до орбитального центра B, а также определить линию апсид, то есть диаметра, на котором лежат А, B и С. Однако АB могла быть определена только в том случае, если бы была известна действительная гелиоцентрическая долгота Марса по отношению к точке А (но не ранее названная «гелиоцентрическая долгота» Марса, которая на самом деле определялась по отношению к точке С). Поэтому Кеплер более не мог опираться только на теории Тихо; и он смело возвращается к ранее отвергнутым им же hypothesis vicaria, а ошибку, вытекавшую из их применения, пытается компенсировать грубым приближением в вычислениях. В результате он пришёл к следующему выводу: Земля и Марс движутся по круговым орбитам с разделённым эксцентриситетом; две эксцентрические точки C и А (рис. 1) лежат на одной линии апсид, находясь на равном расстоянии от центра окружности по разные её стороны.

Что же в конечном счёте было основанием для такого вывода? Теоретические воззрения, проблематичные даже для самого Кеплера: 1. Теории Тихо (включая утверждения о гелиоцентрических положениях Марса и Земли) и 2. Hypothesis vicaria самого Кеплера, ранее столь решительно отвергаемые им. К тому же он использовал довольно грубое приближение в вычислениях; кроме того, он руководствовался классически-философским допущением о круговом движении небесных тел наряду с данными наблюдений Тихо, считавшимися почти непогрешимыми.

Но ни догматы, ни проблематичные допущения не помешали Кеплеру сделать следующий смелый шаг в сторону не только от Птолемея, но и от Коперника. Он отказывается от попыток строить эквантную окружность, то есть решать задачу, навязанную традицией, и вместо этого пытается выявить закономерность, объясняющую неравномерность орбитальной скорости Земли, вращающейся вокруг Солнца. Снова прибегнув к приближениям, он вычислил, что скорость Земли в точках перигелия и афелия обратно пропорциональна расстояниям до Солнца в этих точках. Этого минимума эмпирических данных оказалось достаточно, чтобы сразу же идти дальше, экстраполируя все точки на орбитальной кривой и распространяя этот вывод на все планеты. Таким образом, Кеплер формулирует следующие универсальные положения:

1. Все планеты движутся по круговым орбитам с разделённым эксцентриситетом; Солнце находится в одной из точек эксцентриситета.
2. Скорость планет обратно пропорциональна их расстояниям от Солнца.

Второе положение — так называемый закон радиуса.

Обращает на себя внимание не только спекулятивный характер этого закона, но и то обстоятельство, что Кеплер вообще искал такого рода закономерности, оставив попытки построения эквантной окружности. Тем самым он уже отошёл от аксиомы Платона, то есть от утверждения, что планеты движутся с постоянной угловой скоростью. Определяющим здесь было его мистическое отношение к Солнцу. Воображаемые точки, вокруг которых, как считалось, вращаются небесные тела, были для него чем-то призрачным. Его тревожило уже то, что в системе Коперника Солнце на самом деле не находилось в центральной точке (и потому она не могла быть названа «гелиоцентрической» в строгом смысле) ⁴⁸ и выполняло лишь вспомогательную роль источника света. Для Кеплера же Солнце представляло собой священный центр Вселенной, воплощение Бога-Отца. Поэтому от Солнца должна была исходить сила, заставлявшая планеты кружиться вокруг него (Кеплер связывал её со Святым Духом, а неподвижные звёзды — с Богом-Сыном). Поэтому так важно было определить эту силу, и поэтому вычислению подлежало движение планет по отношению именно к Солнцу, а не к воображаемой точке в пространстве.

Именно эта страстная убеждённость в гелиоцентризме дала Кеплеру возможность искать и находить нечто вроде закона радиуса, а непоколебимая уверенность, выросшая на почве возрожденческого гуманизма, в том, что принципы устройства Вселенной постижимы для человеческого разума, придавала ему смелость, позволявшую видеть в рискованных экстраполяциях силу доказательства. Вдохновляемый своей философией, он неотступно продвигался вперёд, приступив к решению задачи, которая не могла не казаться аристотелианцам изумительной дерзостью — связать закон радиуса с принципом рычага, а затем с гилбертовским магнетизмом, тем самым связывая небесные и земные движения. Отсюда уже было недалеко до воззрения на Вселенную не как на подобие божественной формы жизни (instar divine animalis), а как на подобие часового механизма (instar horologii) ⁴⁹.

Однако в своей гипотезе о причинах движения планет, которую можно было бы рассматривать как предвосхищение теории тяготения Ньютона, он вновь возвращается к аристотелизму, абсолютно противопоставляя покой и движение (он полагал, что если бы не сила, генерируемая Солнцем, то движение планет из-за их естественной инерции остановилось бы). Это закрывало ему путь к закону инерции и, следовательно, как мы теперь понимаем, к наиболее важному аргументу в пользу идеи Коперника. После размышлений над небесной механикой он вернулся к теории движения Марса.

Рассмотрим рис. 2.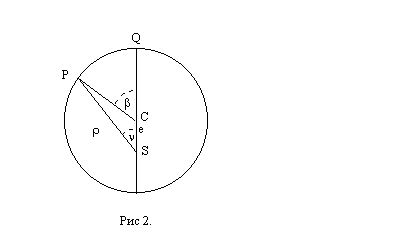

По закону радиуса скорость планеты в точке P на орбите с центром C обратно пропорциональна расстоянию = PS до Солнца S: следовательно, время, затрачиваемое на движение в этом сегменте, пропорционально PS. Но как выразить эту зависимость точной формулой? Казалось невозможным найти прямое отношение между радиусом и временем движения.

И здесь Кеплер вспомнил так называемую теорему Архимеда, выражающую отношение площади круга и радиуса окружности. Согласно этой теореме площадь сектора QCP можно рассматривать как предел суммы бесконечного числа бесконечно малых треугольников с высотой, равной радиусу окружности. Это подсказало Кеплеру идею связать время, за которое планета проходит путь PQ, не непосредственно с радиусом окружности, а 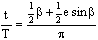с площадью сектора, описываемого радиус-вектором. Не долго думая, он применил теорему Архимеда, благодаря чему в его распоряжении оказалось достаточно сомнительное средство выражения через площадь, описываемую отрезком CP (то есть радиус-вектором орбиты) времени, необходимого для прохождения планетой соответственной дуги орбиты, и тем самым он получил по крайней мере косвенную возможность выразить соотношение времени и радиус-вектора в следующей формуле:

(1)

Где t — время прохождения планетой дуги PQ, а Т — время, затрачиваемое планетой на прохождение всей орбиты. Если r = 1, то площадь QCP = ½, площадь CSP = ½ e sin, а — площадь круга.

Из [1] следует:

(2)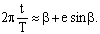

Может быть вычислено, если известно t (хотя методы, которыми располагал Кеплер, могли давать только грубое приближение).

Итак, расстояние между планетой и Солнцем определяется уравнением:

(3)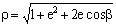

Получаемым, в соответствии с р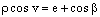ис. 2 по закону косинусов. Наконец, из этого следует уравнение:

(4)

Из которого по простому отношению косинусов выводится значение v, и, следовательно, положение планеты в момент времени t.

В этих рассуждениях используются: 1) закон радиуса, с помощью которого устанавливается отношение между временем и радиусом; 2) модификация теоремы Архимеда, посредством которой от вывода площади сектора круга, описываемого радиус-вектором, переходят к вычислению площади QSP, то есть чего-то совершенно отличного от сектора круга. Таким образом, отношение между временем и радиус-вектором преобразуется в отношение между временем и площадью круга. Едва ли можно говорить об эмпирических основаниях закона радиуса, а указанный переход от теоремы Архимеда к её модификации не был обоснован математически. И то, и другое было хорошо известно Кеплеру. К этому надо добавить, что в уравнениях 1–4 фигурирует эксцентриситет e, что стало возможным только благодаря hypothesis vicaria, которые Кеплер вначале отвергал.

Таким образом, и на этой стадии исследований Кеплер вновь показал, что его не слишком заботила точность и достаточность эмпирического, математического или теоретического обоснования, хотя, как это видно из отрывка, приведённого в начале этой главы, их возможность им предполагалась. Поэтому нет ничего удивительного в том, что, исходя из минимума эмпирических данных, он в конечном счёте отказался и от остававшейся части аксиомы Платона — от допущения о круговой форме планетарных орбит — как ранее он отказался от другой её части, от допущения о постоянстве угловой скорости планет.

На этот шаг он решился в ходе новой попытки определить орбиту Марса. Вначале Кеплер применил уже описанный метод, использованный при вычислении орбиты Земли. Так же как тогда он сравнивал различные положения Земли по отношению к константному положению Марса, так и теперь три различных положения Марса соотносятся им с одним и тем же положением Земли. Тем самым были определены три расстояния Марса от Солнца и три угла, образуемых соответствующими радиус-векторами. С помощью утомительных, хотя и простых, тригонометрических вычислений он определил линию апсид и значение эксцентриситета Солнца для трёх различных случаев. Все результаты были различны. Из этого мог быть сделан только один вывод: орбита Марса не может быть круговой.

Этот революционный для астрономии вывод был сделан на основе тех же смелых допущений, как и при вычислении орбиты Земли. Почва, на которой теперь стоял Кеплер, была не менее зыбкой, чем раньше: теория Тихо, hypothesis vicaria и вера в правильность данных Тихо.

И на заключительной стадии исследования, когда он пришёл к заключению, что орбиты планет должны иметь форму эллипса, спекулятивный дух ему не изменил. Обратимся к 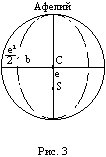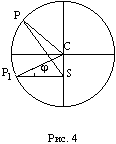рис. 3.

Прежде всего, следуя принципу простоты, Кеплер постулировал отклонение орбиты Марса от круговой формы по формуле b = 1-e², где 1 — радиус, e — эксцентриситет Солнца, b — ось действительной орбиты. Позднее он представил b = 1 − (e²/2).

Но однажды он сделал открытие, суть которого мы сможем понять, взглянув на р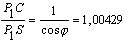ис. 4, представляющий орбиту Марса. Он заметил, что:

(5)

Здесь — наибольший угол, образованный схождением сегмента P₁ S (планета-Солнца) и P₁ C (планета-центральная точка окружности). Если затем просто подставить предполагаемое значение b в вычисления, то получится: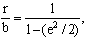

А поскольку e <1, то: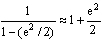

Но 1 + (e²/2) равно 1.00429, что согласуется с вычисленным результатом [5].

«Когда я увидел это, — писал Кеплер, — я словно бы очнулся ото сна и увидел свет» ⁵⁰.

Полученное отношение, хотя оно было лишь приблизительным и верным только благодаря малости e, немедленно вдохновило его на новые спекуляции, представленные 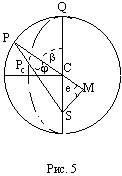рис. 5.

Он предположил, что (см. Pис. 5) отношение, аналогичное 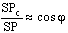уравнению [5] должно выглядеть следующим образом:

Иначе говоря, отношение расстояния между Солнцем и планетой на «истинной» орбите к расстоянию между Солнцем и планетой на «воображаемой» орбите аналогично отношению r/b на рис. 3.

При r = 1 получаем:

SP cos = PM PM = 1 + e cos.

Из этого следует, что планетарные орбиты выражаются формулой:

(6)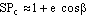

После изнурительных трудов — «paene usque ad insanium» — Кеплер установил, что уравнение [6] выражает формулу эллипса, хотя и приблизительно (надо напомнить, что математический аппарат, доступный Кеплеру, был ещё достаточно примитивен).

Итак, и на этой стадии, как мы видим, Кеплер вновь прибегает к использованию предположений, спекуляций и грубых приближений; более того, проверка уравнения [6] предполагает сравнение значений SP_e с теми значениями, которые были получены методами определения расстояния, применяемыми Кеплером; критические замечания об этих методах были сделаны выше.

В заключение рассмотрим ещё один шаг Кеплера (см. Pис. 6).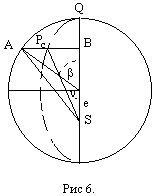

В соответствии с ф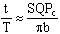ормулой [1] здесь также должно выполняться соотношение:

(7)

Другими словами, время t, необходимое, чтобы планета прошла по эллиптической дуге QP_c, относится ко времени T, затрачиваемому на прохождение всей орбиты, так, как площадь SQP_c относится к общей площади эллипса, где b — радиус малой оси, а большая ось принята за 1. Здесь Кеплер делает предположение, аналогичное тому, какое уже было сделано ранее (см. Pис. 4 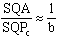и 5):

(8)

Согласно [1].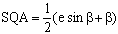

Если подставить это значение 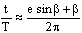в [8] и [7], то в результате простых вычислений получим:

Решающий шаг в этом выводе — принятие за исходный пункт уравнения [7] — есть не что иное, как новое и не менее проблематичное применение теоремы Архимеда; теперь она применяется к сектору эллипса, вершиной которого является один из его фокусов, в котором помещается Солнце.

Теперь можно сформулировать два первых закона Кеплера [ср. у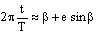равнение [6]]:

(9)

(10)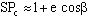

Уравнение (10) говорит о том, что планета движется по эллипсу, в одном из фокусов которого находится Солнце. Уравнение [9] говорит, что в равные промежутки времени радиус «Солнце-планета» пробегает равные площади.

По отношению к Марсу, который является центральной проблемой и исходным пунктом всех рассуждений, это означает, что b и e в уравнении [9] могут быть определены только благодаря ранее отброшенным (даже в усовершенствованном виде) hypothesis vicaria. Поэтому они использовались как при вычислениях SP_с, так и в методе оценки и проверки полученного результата (включая определение трёх положений Марса по отношению к одной и той же позиции Земли).

Вот как в действительности обстояли дела с обоснованием двух первых законов Кеплера, обоснованием, которое ещё и сегодня часто представляют чем-то таким, что возникло исключительно на базе опыта.

Кстати сказать, теория Птолемея в сравнении с теорией Кеплера вовсе не проигрывает, ибо, во-первых, из-за малости орбитальных эксцентриситетов планет система Птолемея описывает движения планет почти с той же точностью, как теория Кеплера (что же касается Меркурия, то он является для обеих теорий своего рода enfant terrible); во-вторых, аксиома Платона имела ясное философское обоснование, тогда как для Кеплера эллиптическая форма планетарных орбит, естественно, оставалась загадкой. Его попытка обосновать эту форму спецификой движений планет не привела к успеху. В-третьих, то же можно сказать о его усилиях опровергнуть аристотелианскую аргументацию против идеи вращения Земли. Всё это было типичными гипотезами ad hoc ⁵¹. Неудивительно, что его «Новая астрономия» была встречена современниками без всякого энтузиазма.

Анализ методов и доказательств, фигурирующих в «Новой астрономии», позволяет нам сказать со всей определённостью: если бы Кеплер следовал доктринам, принятым в теории науки нынешнего времени, он должен был бы отбросить оба своих закона, значимость которых вряд ли кто-либо сегодня осмелится отрицать. Покажем это на двух примерах: методологии науки Поппера-Лакатоса и индуктивной логики Карнапа.

5.2. «Новая астрономия» Кеплера в свете философии науки Поппера и Лакатоса

Основной методологический постулат Поппера гласит, что научная теория должна быть фальсифицируемой. Если же фальсификация уже произошла, нам не следует предотвращать крах теории с помощью гипотез ad hoc или других допущений. Поппер пишет: «Если такое решение положительно, то есть если сингулярные следствия оказываются приемлемыми, или верифицированными, то теория может считаться в настоящее время выдержавшей проверку, и у нас нет оснований отказываться от неё. Но если вынесенное решение отрицательное или, иначе говоря, если следствия оказались фальсифицированными, то их фальсификация фальсифицирует и саму теорию, из которой они были логически выведены» ⁵².

О каком «решении» здесь идёт речь? Этот термин означает, что так называемые базисные предложения (под которыми Поппер понимает сингулярные экзистенциальные предложения типа: то-то и то-то существует в такой-то и такой-то пространственно-временной области) ⁵³ противоречат или не противоречат данной теории. Но если теории противоречат только отдельные сингулярные базисные предложения, у нас ещё нет основания считать теорию фальсифицированной. «Мы будем считать её фальсифицированной только в том случае, если нам удалось открыть воспроизводимый эффект, опровергающий теорию. Другими словами, мы признаем фальсификацию только тогда, когда выдвинута и подкреплена эмпирическая гипотеза низкого уровня универсальности, описывающая такой эффект. Подобные гипотезы можно назвать фальсифицирующими гипотезами» ⁵⁴.

В качестве примера Поппер приводит высказывание «В нью-йоркском зоопарке живёт семейство белых воронов» ⁵⁵; оно фальсифицирует универсальное высказывание «Все вороны чёрные». Но, добавляет он, «в большинстве случаев до фальсификации некоторой гипотезы мы имеем в запасе другую гипотезу, поэтому фальсифицирующий эксперимент обычно является решающим экспериментом, который помогает нам выбрать одну из двух гипотез» ⁵⁶.

Итак, фальсифицирующий эффект выводится из другой гипотезы, уже имеющейся в запасе. Конечно, поскольку такого рода решения опираются на базисные предложения, они принципиально могут быть пересмотрены (опять-таки с помощью базисных предложений); но практически мы обычно в какой-то момент прекращаем поиск опровержений и пытаемся закрепиться на избранной позиции. Поэтому Поппер вводит следующее правило: «Мы раз и навсегда отказываемся от того, чтобы приписывать какую-либо подтверждающую силу теории, фальсифицированной в ходе интерсубъективно проверяемого эксперимента» ⁵⁷.

Однако Кеплер поступал как раз наоборот, когда он использовал результаты ранее фальсифицированных теорий для построения других теорий и затем оценивал последние с помощью первых. Кроме того, он находился в явном противоречии с попперовской методологией ещё и в другом отношении. В то время отсутствие каких-либо явлений, указывающих на вращение Земли, рассматривалось как фальсификация всякой формы гелиоцентризма. Чтобы обойти эту фальсификацию, Кеплер пытался делать то, что решительно запрещает Поппер ⁵⁸, а именно: спасти свою теорию с помощью гипотез ad hoc — и кроме того, с помощью гипотез, не менее проблематичных, чем его астродинамика. Следуй он предписаниям Поппера, ему пришлось бы отказаться от своей теории «раз и навсегда».

Сам Поппер полагает, что успех Кеплера оказался возможным отчасти потому, что «гипотеза окружности, от которой он отталкивался в своём исследовании, была относительно легко фальсифицируемой» ⁵⁹. Он прав в той мере, в какой выражение «относительно легко» связано с тем, что гипотеза окружности являлась «трёхмерной» («поскольку для её фальсификации необходимы по крайней мере четыре принадлежащих данной области сингулярных высказывания, соответствующих четырём точкам её графического представления» ⁶⁰), тогда как эллиптическая гипотеза являлась «пятимерной» («поскольку для её фальсификации необходимы по крайней мере шесть сингулярных высказываний, соответствующих шести точкам на графике» ⁶¹). Однако рассуждения способны скорее лишь завуалировать тот факт, что фальсификация гипотезы о круговой орбите была в высшей степени проблематичной, ибо основана она была на весьма сомнительных посылках.

Пример Кеплера свидетельствует не только о том, что фальсифицирующие базисные предложения трудно распознать (эта трудность, я считаю, не была в достаточной мере осознана Поппером ⁶²), но и о том, что отбрасывание теории в каждом случае, когда фальсификация может быть установленной, вовсе не всегда является лучшей стратегией для науки ⁶³.

До сих пор мы сравнивали методологию Кеплера с тем, что сегодня может быть названо классическим попперианством. Однако наши выводы остаются в силе даже с учётом тех улучшений, которые были внесены в эту концепцию И. Лакатосом в последние годы.

По его мнению, существует универсальное правило, по которому можно определить, является ли серия теорий прогрессивной (Конечно, он совершенно прав, когда говорит о «серии», а не о единичных теориях, ведь фактически каждая теория связана с другими, отличными от неё теориями).

Он пишет: «Будем считать, что такой ряд теорий является теоретически прогрессивным…, если каждая новая теория имеет какое-то добавочное эмпирическое содержание по сравнению с её предшественницей, то есть предсказывает некоторые новые, ранее не известные факты. Будем считать, что теоретически прогрессивный ряд теорий является также и эмпирически прогрессивным…, если какая-то часть этого добавочного эмпирического содержания является подкреплённым, то есть если каждая новая теория ведёт к действительному обнаружению новых фактов. Наконец, назовём сдвиг проблем прогрессивным, если он и теоретически, и эмпирически прогрессивен, и регрессивным — если нет» ⁶⁴.

Здесь приходится снова отметить, что Кеплеру пришлось бы отбросить свою теорию, если бы следовал правилу Лакатоса. Кеплер мог, правда, благодаря своей теории предсказать некоторые новые, ранее неизвестные факты; но, с другой стороны, ещё большее количество фактов, которые вполне согласовались с астрономией Птолемея и физикой Аристотеля, он не мог объяснить. К этим фактам, в первую очередь, относятся явления, которые — из-за отсутствия разработанного принципа инерции — заставляли отрицать вращение Земли. Поэтому нельзя утверждать, что теория Кеплера имела «дополнительное эмпирическое содержание» по сравнению с предшествовавшими ей теориями.

Это, однако, ещё не все. Само подтверждение фактов, предсказанных Кеплером, было, как уже отмечалось выше, в высшей степени проблематичным. Мы уже видели, к примеру, что для вычисления орбиты Марса Кеплеру понадобились hypothesis vicaria и что полученные результаты он проверял методами, основанными все на тех же гипотезах. Кеплер и сам вполне осознавал эти недостатки, поэтому и прибегал к допущениям более метафизического и теологического характера (к этому моменту мы ещё вскоре вернёмся). Может ли правило Лакатоса чем-либо помочь при решении вопроса о допустимости всех этих предпосылок?

Очевидно, выражение «предсказание факта» не так ясно и просто, как представляется Лакатосу. Можно ли усматривать в предсказании факта теоретический прогресс, особенно когда предпосылкой такого предсказания является нечто рискованное, проблематичное или попросту глупое? Что касается открытия Кеплера, то разве сама приемлемость его предсказаний не ставится под вопрос тем фактом, что предпосылками их являются метафизические и теологические рассуждения? И разве не по той же причине под вопросом остаётся именно сама возможность признания результатов его проверочных процедур? Речь же действительно идёт не о проверке фактов и не о возможности предсказаний, а о том, являются ли основания таких предсказаний и предпосылки проверочных процедур ясными и очевидными. Но об этом правило Лакатоса ничего не говорит.

Представим себе на мгновение Лакатоса в роли Великого Инквизитора, который во времена Кеплера должен был следить за развитием науки, руководствуясь своей собственной «установкой». Допустим, что он допрашивает Кеплера, и прислушаемся к их диалогу:

Лакатос: Способен ли ты обеспечить своей теории добавочное эмпирическое содержание по сравнению с содержанием её предшественниц?

Кеплер: Да, я действительно могу кое-что объяснить, хотя, сознаюсь, Птолемей и Аристотель далеко превосходят меня в этом.

Лакатос: Можешь ли ты предсказать что-нибудь новое?

Кеплер: Могу, но если ты принимаешь те основания, на которых строятся мои предсказания, и, кроме того, признаешь допущения, необходимые для подтверждения фактов.

Лакатос: Каковы же эти допущения?

Кеплер: Они весьма проблематичны, так как их можно принимать только в сфере астрономии.

Лакатос: Анафема.

Кеплер: Позволь мне сказать последнее слово. Две предпосылки, принятые мной, имеют крайне важный смысл, в который я искренне верю. Одна из них заключается в том, что Коперник наверняка прав, потому что его картина мира гораздо проще других и потому что она соответствует духу человечности и духу Божественной Справедливости. Второе — Земля не может быть одновременно центром Вселенной и юдолью греха. Поэтому я верю в то, что именно Солнце — это звезда, вокруг которой вращаются все прочие. Если признать это, то остальное, какие бы проблемы здесь ни возникали, приобретает рациональный смысл.

Лакатос: Все это не имеет никакого научного значения. Итак, повторяю: анафема.

Бедный Кеплер! Ему непременно пришлось бы отречься от своей теории, последуй он правилу Лакатоса ⁶⁵.

5.3. «Новая астрономия» Кеплера и индуктивная логика Карнапа

Теперь посмотрим, как выглядит теория Кеплера в свете индуктивной логики Карнапа. С помощью этой логики определяется степень подтверждения гипотезы h релевантными данными e. Элементарным её выражением является поэтому c (h, e) = r, где c — степень подтверждения, r — численное значение из интервала (0,1).

Разумеется, индуктивная логика Карнапа разработана применительно к языкам более примитивным, чем теория Кеплера. Но это не мешает нам задаться вопросом, могла ли эта логика использоваться Кеплером и что получилось бы из этого. Карнап признавал, что в основе его логики лежат упрощения и идеализации, которые следует рассматривать как неизбежную дань всякому логическому начинанию. На последующих стадиях, считал он, можно надеяться на построение всё более сложных систем индуктивной логики, которые позволили бы определять степени подтверждения физических теорий и гипотез. Простейшая исходная конструкция может рассматриваться как более или менее грубое «приближение» к более сложным ⁶⁶. То, что представляется чрезвычайно сложным практически, не является в силу этого принципиально невозможным в теории. Здесь, видимо, уместно вспомнить замечание Карнапа о том, что «все учёные, если отвлечься от деталей, используют один и тот же индуктивный метод, близкий к тому, который основывается на моей функции C» (так Карнап обозначает результат выбора из возможных процедур подтверждения в индуктивной логике) ⁶⁷.

Хотя ещё не существует формальной системы, которая позволяла бы определить точную степень подтверждения гипотезы Кеплера и его законов, легко понять, что, если бы значение этой функции было вычислено в рамках примитивного языка индуктивной логики, оно оказалось бы чрезвычайно малым. Мы говорили о том, что гипотезы Кеплера имели очень слабое эмпирическое подтверждение, что Кеплер прибегал к «предиктивным выводам» (выражаясь в терминологии индуктивной логики) весьма рискованного характера — от наблюдений нескольких планет к утверждениям, относящимся ко всем планетам, от двух определённых точек орбиты — к конфигурации орбиты в целом и так далее; ⁶⁸ что процедуры проверки («e» в индуктивной логике) включали в себя гипотезы, которые, в свою очередь, оказывались составными частями гипотезы «h», подлежащей этим проверкам, и так далее. Следовательно, если смотреть сквозь призму индуктивной логики Карнапа, рассматривая её примитивные языки и функции как модель — а это, как также уже было показано, мы можем себе позволить, — то придётся заключить, что Кеплер, будь он знаком с этой логикой и приняв на себя её обязательства, вряд ли отважился бы на формулировку своих первых двух законов и их защиту.

Кажется, что этому противоречит тот факт, что сам Карнап предостерегал от отождествления индуктивно-логических и методологических выводов ⁶⁹. Определение степени подтверждения, указывал он, само по себе никак не решает проблему принятия или отбрасывания гипотез, поскольку эта проблема относится к методологии. Например, вероятность выигрыша в лотерее какого-либо конкретного номера является минимальной, но нет ничего иррационального в том, что мы покупаем билет с этим номером и надеемся выиграть. Всякий раз, когда принимается решение относительно гипотезы, в определение степени подтверждения должны, по-видимому, входить и другие основания, уже не относящиеся собственно к индуктивной логике. Карнап использует для описания таких оснований довольно туманные выражения: «практические решения» ⁷⁰, «жизненные ситуации, в которых наблюдаем, судим и принимаем на веру» ⁷¹, «нелогические факторы» ⁷² и другие.

Однако даже если индуктивная логика и методология — не одно и то же, то в соответствии с концепцией Карнапа они всё равно связаны друг с другом. Он пишет: «методология… разрабатывает процедуры, позволяющие использовать результаты индуктивной логики в конкретных целях» ⁷³. С другой стороны, индуктивная логика не мешает учёному учитывать вненаучные факторы при принятии решений; напротив, она облегчает эту задачу ⁷⁴. Действительно, какой смысл имела бы индуктивная логика, если бы она была бесполезна в процессах принятия решений, как теоретических, так и практических?

Было бы слишком большой роскошью оправдывать существование такой логики только тем, что она позволяет определить «истинное» или «чистое» отношение между h и e, оставаясь при этом совершенно равнодушной к вопросу о том, как это отношение могло бы найти практическое применение? В отличие от дедуктивной логики, высказывания индуктивной логики сами по себе не общезначимы; более того, уже сами её аксиомы намеренно подбираются таким образом, чтобы они могли служить теоретическими и практическими ориентирами исследователя, быть адекватными научному методу ⁷⁵.

Соглашаясь с Карнапом в том, что индуктивная логика и методология не суть одно и то же, мы должны — и здесь следуя за ним — потребовать, чтобы они не были отделены друг от друга китайской стеной, чтобы методология находила подкрепление в индуктивной логике. Поэтому, когда методология никаким образом не использует результаты индуктивной логики и даже прямо отвергает их (о чём говорит пример Кеплера), то это не может не дискредитировать её именно как «логику». Поэтому и Карнапу также приходилось ещё больше уточнять упомянутое выше предостережение. По его мнению, действия учёных направляются численными значениями «степени подтверждения» (если даже эти степени не выражены эксплицитно); например, высокая подтверждённость гипотезы может побудить учёного вложить крупную сумму денег в исследовательский проект или экспериментальную программу, и так далее ⁷⁶.

Штегмюллер, видимо, также преследовал методологические цели, когда он с одобрения Карнапа писал о том, что выводы об индуктивной вероятности способны направлять нас к рациональным действиям ⁷⁷; что индуктивная логика способна повлиять на выбор учёным теоретической гипотезы, хотя это влияние не может быть определяющим; ⁷⁸ что индуктивная логика помогает принимать решения не вслепую, но с пониманием дела ⁷⁹. Индуктивная логика определяет степень подтверждённости гипотезы данными, а методология должна использовать эту информацию, помещая её в более широкий контекст обоснования.

Таким образом, Карнап всё же строго разделял индуктивную логику и методологию, в особенности, когда речь шла о принятии практических решений (например, в ситуации пари); однако он не возражал против того, что индуктивная логика и методология тесно связаны между собой в теоретической области ⁸⁰. Эмпирически недостаточно или слабо подтверждённые гипотезы, по его мнению, вряд ли могут претендовать на теоретическое признание.

Следовательно, Кеплер, если бы он разделял такое представление об индуктивном анализе, вынужден был бы отвергнуть свою теорию или, по крайней мере, считать её в высшей степени сомнительной.

Возразят, что в примере с Кеплером мы имеем дело с начальной, гипотетической, пробной формулировкой теории, то есть с теорией на первой стадии её развития, тогда как индуктивная логика должна применяться к вполне развитым теориям, таким как классическая механика, оптика, и так далее. Но по своему замыслу индуктивная логика должна работать с любым отношением h и e, когда оно рассматривается как логическое отношение; поэтому, если доступная информация, фигурирующая в e, достаточно дифференцирована и понятна, она всегда может найти методологическое применение. Следовательно, Кеплер имел право применить индуктивную логику к своей теории.

К тому же что означает «вполне развитая теория?» Кто знает в какую сторону пойдёт это развитие и как будет выглядеть принятая сегодня конкретная теория через сто лет? Во всяком случае Кеплер не рассматривал свои результаты лишь как начальную или пробную попытку; он полагал, что эти результаты совершенны в той мере, в какой это возможно, то есть основаны на вполне развитом астрономическом знании его времени. Исследователь всегда принимает свои решения «здесь» и «теперь». А индуктивная логика либо должна помогать ему в такой ситуации, либо она вообще ему не нужна.

5.4. Недостаток чувства исторического у Поппера и Карнапа

Предыдущие рассуждения подвели нас к выводу, что ценность индуктивной логики по отношению к принятию научных решений проблематична и что фальсификационизм Поппера не всегда выступает адекватным методом науки. Исследовательские действия Кеплера противоречат тому, в чём Карнап и Поппер видят идеалы «теоретико-научного разума».

Обнаруживается, что Кеплер, напротив, вдохновлялся мистикой Солнца (в чём при желании можно усмотреть некое аксиоматическое установление, если принять терминологию предшествующей главы) и умозрительной идеей о познаваемости принципов устройства Вселенной (нормативное установление). Оба эти установления заимствованы им у Коперника и оба они связаны с духом Возрождения. Мистика Солнца и умозрительная идея были источником его абсолютной веры в гелиоцентрическую систему и в возможность полного описания этой системы как «истинных движений» небесных тел. Для этой цели не было более подходящих теорий, чем те, которые разработал Тихо, и не было более приемлемых гипотез, чем hypothesis vicaria, а раз так, то нужно было заставить работать именно эти теории и эти гипотезы — ведь истина так или иначе должна открыться человеку. По тем же причинам данные наблюдений тоже должны были считаться абсолютно надёжными (оправдательное установление). Солнце было символом Бога-Отца, поэтому именно оно обладало первостепенным значением при попытке определить связь между ним и Землёй; значит, нужно было использовать все имевшиеся средства, чтобы выяснить точную структуру этой связи, будучи абсолютно убеждённым в выполнимости такой задачи.

Когда Кеплер экстраполировал два вычисленных значения на все прочие точки определяемой орбиты, им руководила вера в Божественную Милость, которая должна была прийти ему на помощь в поиске знания о Вселенной; именно она позволяла ему пускаться в необоснованные математические аналогии, принимать в качестве обоснований допущения, страдающие пороком логического круга, или фальсифицированные теории. Поэтому в конечном счёте Кеплер требует от своего читателя, чтобы тот соглашался с мистическими и умозрительными предпосылками астрономических рассуждений, принимал правила его метода, заранее разделял его априорную уверенность в гелиоцентризме.

Путь, которым шёл в науке Кеплер, можно было бы сравнить с движением лунатика, поддерживаемого таинственным влечением, которое предохраняет его от падений, какими бы сильными не были внешние толчки. Но когда, наконец, Кеплер достиг своей цели, создав совершенно новую астрономическую концепцию, он столкнулся с гораздо более серьёзными трудностями, чем те, с какими он встречался вначале. Сравнивая «Новую астрономию» с системой Птолемея, мы вынуждены спросить себя, почему картина Вселенной, в основу которой были положены некоторые гуманистические начала, должна считаться более понятной, более приемлемой в интеллектуальном отношении? Как уже было отмечено, эллиптическая форма планетарных орбит приводила в замешательство и Кеплера, и его современников.

И тем не менее, как мы видели, Кеплер принимает новые установления в своих исследованиях и строит новую систему понятий, с помощью которой упорядочивает и объясняет природу. Однако сама эта система берётся им не из природы, её корни уходят в историю культуры.

Поэтому как бы ни различались теории науки Поппера и Карнапа их общим и фундаментальным недостатком является неисторичность. То же можно сказать и о других современных теоретико-научных концепциях; в них нет понимания исторических оснований научного прогресса, которое требует выхода за непосредственные границы понятийного аппарата современной науки. Такое понимание возникает только в процессе изучения истории науки. На примере Кеплера мы убеждаемся в том, что изучение истории способно внести коррективы в те методологические построения, которые основываются на слишком поспешном принятии некоторых постулатов и обобщений, как это было показано в предыдущей главе.

До недавнего времени исследования Кеплера и та линия, которая связывает их с Ньютоном, рассматривались совершенно иначе. На этом примере пытались показать, что неизменные научные методы и адекватный эмпирический материал сами собой обеспечивают прогресс в физике; наблюдение природы с помощью этого метода считалось чем-то самодостаточным, тогда как истории, в особенности истории культуры, не отводилось какой-либо серьёзной роли в этом прогрессе. Это порождало убеждение, что Кеплер пришёл к своим законам чисто эмпирическим путём, а ньютоновский закон всемирного тяготения был результатом индуктивного обобщения исследований Кеплера.

Теперь стало ясно, что в законах Кеплера следует усматривать не эмпирические обобщения, а гипотезы, опиравшиеся на крайне сомнительные допущения. Далее, эти законы имеют чисто кинематический характер — в них не фигурируют ни массы, ни силы — и потому из них невозможно чисто индуктивно вывести общий закон динамики, закон всемирного тяготения. Но главное в том, что в строгом смысле законы Кеплера противоречат механике Ньютона, так как в ньютоновской картине мира массы тяготеют друг к другу и вращаются вокруг гравитационного центра системы, который не совпадает с центром Солнца, а, по Кеплеру, именно Солнце находится в фокусе эллиптических орбит. Следовательно, Ньютон изменил считавшийся эмпирическим факт, из которого якобы выросла его теория, придав эмпирическим наблюдениям новую динамическую интерпретацию, спонтанность которой указывает на наличие новых философских оснований и на историческую трансформацию установлений.

Поэтому линия, связующая Кеплера с Ньютоном, вопреки расхожему мнению является аргументом в пользу не аисторической теории науки, а теории науки, ориентированной на историю науки ⁸¹.

В заключение скажем следующее: теория науки без истории науки пуста, а история науки без теории науки слепа ⁸². Приведённый пример показывает это совершенно отчётливо.