50. Резюме предыдущего. Идея последовательного развёртывания множества разных схемНаша сегодняшняя лекция будет значительно труднее, чем предыдущая. Если раньше мы рассматривали и обсуждали с вами разные фрагменты и элементы общей картины, то сегодня её предстоит взять уже в целом. То, что мы обсуждали раньше, нам придётся собрать вместе и начать применять. Если Итак, мы имеем по крайней мере две области работы — собственно предметную, которая будет изображаться нами слева, и методологическую, которую мы будем изображать справа. В предметной области мы имели дело по крайней мере с двумя существенно различными явлениями (на самом деле — с большим числом). Эти два явления были различны. Мы обнаружили это благодаря тому, что в некоторых случаях две схемы, выработанные нами, могли прикладываться друг к другу, характеризуя временную последовательность событий. А в других случаях — прикладывание схем друг к другу не могло истолковываться как изображение временной последовательности событий. Из этого мы сделали вывод, что в интересующей нас области существуют явления, по крайней мере, двух типов. Одно из них описывается параметрическими признаками а, р1, у, а другое — параметрическими признаками а, 8, е. Но, очевидно, — мы производим здесь некоторое обобщение — у нас и дальше будут набираться в эмпирическом материале все новые и новые явления, которые, в принципе, будут характеризоваться какими-то другими признаками или свойствами, скажем, свойствами α, φ, ψ и так далее. Кроме того, мы взяли определённые рабочие схемы и, прикладывая их друг к другу, составили определённые структурные изображения. Напомню вам, что элементы в них предполагаются одинаковыми — об этом свидетельствуют индексы при элементах, связи — разными. Надеюсь, вы помните, что в нашем случае речь шла о связях управления или аналогичных им. Мы составили подобную структурную схему, и она объясняет, по крайней мере, два выделенных нами явления: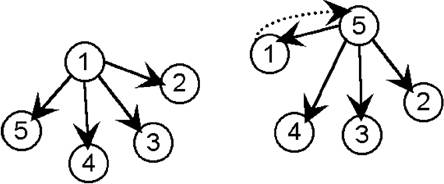
Мы определили эту схему как рабочую; пока она не может претендовать на звание теоретической. Но далее перед нами стоит задача построить собственно теоретическую систему, описывающую все явления такого рода, то есть любые малые группы и взаимоотношения людей в них. В принципе, мы должны ориентироваться на однообразные схемы и притом на сравнительно небольшую группу их. Вообще говоря, можно было бы описывать первое явление в одних схемах, а второе явление — в других. Подобное знание сильно напоминали бы знания по математике, которые существовали у древних вавилонян и египтян. Но ясно, что таким образом организованные знания были бы по меньшей мере не компактными, их организация была бы не удовлетворительной во многих отношениях. Кстати, нельзя сказать, что эти изображения не были бы истинными. Древнеегипетские алгоритмы расчёта площади трапецеидальных или лункообразных полей ничуть не хуже, в смысле точности и правильности, наших нынешних. Они неудобны и неудовлетворительны по другим параметрам, в частности, от древнегреческих знаний по геометрии их отличает именно неорганизованность. А последняя, как вы знаете, характеризует значительно более высокий слой работы. Атомарные знания древних египтян оказались неудовлетворительными не сами по себе, а как элементы более сложных систем надстраивающейся над ними деятельности. Поэтому сейчас, имея в виду процессы систематизации знаний, мы всегда должны стремиться к тому, чтобы объяснить максимум явлений на основе минимума теоретических схем. Это — требование, внешнее для содержания знаний, вытекающее из дальнейших способов их употребления. Вместе с тем, мы уже затвердили, что два выявленных нами случая существенно различаются, и число различающихся между собой случаев будет дальше всё больше увеличиваться. Значит, наша теоретическая система в целом и её базис — структурные схемы — должны иметь внутренние возможности для развёртывания и все большей дифференциации. Но раз указанные нами явления существенно различны, их нельзя объяснить с помощью одной схемы. Если мы говорим, что эти явления различны, то это, по существу, лишь другое выражение того, что нам нужны разные схемы для их описания. Итак, наша цель — множество разнообразных схем, и вместе с тем, единообразная система объяснения всех явлений. Значит, у нас остаётся только один путь. Все разнообразные схемы, которые мы будем развёртывать — каждая из них будет описывать свой круг явлений — должны быть организованы на базе единых (одного или нескольких) принципов. Схем должно быть много, для каждого особого случая — своя схема, и одновременно, все они должны быть одинаковыми по принципам своего построения или развёртывания. Их всех мы должны единообразным образом получать или конструировать каждый раз, когда нам это нужно. Вспомним теперь разбиравшуюся выше схему с моделями.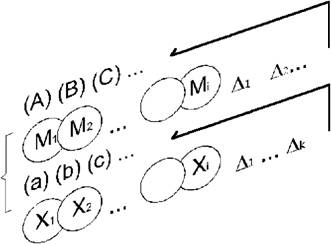
С одной стороны, мы имеем сами объективные явления. Мы фиксируем некоторые характеристики. Кроме того, мы имеем определённую рабочую схему, используемую нами в качестве структурной модели этого и следующих явлений. Из этой схемы-модели мы должны особым образом выводить те свойства, которые мы выявили экспериментально или эмпирически из рассматриваемых нами объективных явлений. Всё это представлено в изображённой выше схеме: Хj — объект; Ai… Ak — эмпирические процедуры анализа его; (а), (в), (с) — признаки его; Ml — набор структурных схем, выступающих в роли модели; A’i … A’i — процедуры, применяемые к ним; (А), (В), (С) — признаки, «полученные» на моделях. Модели, взятые вместе с характеризующими их свойствами, должны всё время соотносится с эмпирическими объектами, взятыми вместе с их свойствами, и в ходе этого соотнесения последние должны объясняться с помощь. Первых. Мера соответствия тех и других — показатель успешности нашего анализа. Но здесь, естественно, возникает вопрос о том, как всё это сделать, то есть каким образом, имея набор эмпирических данных нам явлений с характеризующими их свойствами, с одной стороны, и набор рабочих схем, — с другой, систематическим образом построить теорию, описывающую наш объект — малые группы и взаимоотношения людей в них. Самый естественный путь для человека — посмотреть, как подобные задачи решались в других случаях — в тех, когда теорию удалось построить, и она дала достаточно хорошие результаты. Естественно также, что мы должны искать случаи, в которых описывался примерно такой же по типу объект, с каким мы сейчас имеем дело. Если мы обращаемся к достаточно развитым в настоящее время предметам и объектам таких наук, как физика, то с самого начала обнаруживаем существенное расхождение между ними и тем, что нам приходится рассматривать в теории групп. Возьмём, к примеру, Евклидову геометрию. Рассмотрим более детально объекты, с которыми он имеет дело. Известно, что в начале всего положен треугольник, который строится по определённому заданию, затем появляются прямоугольники, квадраты, треугольники более сложного типа, трапеции и круги. Каждый новый объект строится на основе предыдущего, и вместе с тем знания о новом объекте получаются из знаний о предыдущих. Но при всём при том есть одна особенность, характеризующая эти объекты: каждый из них выступает отдельно, изолированно от других, сам по себе. Эти объекты не образуют каких-либо целостных систем. Ясно, почему. Уже по способу своей «жизни» треугольник никак не связан с квадратом или кругом. Каждый из этих объектов лежит отдельно, живёт своей особой жизнью и даже, как результат конструирования в конечном представлении, выступает как независимое от других. Когда мы рассматриваем группы, то уже при первом самом поверхностном подходе обнаруживаем, по сути дела, другой тип жизни, по меньшей мере, по двум признакам. Покажу их сначала на примерах. Даже если мы выделили игровую группу как некоторую самостоятельную и изолированную целостность, то всё равно мы знаем, что вся система взаимоотношений детей в группе, все их поведение определены другими взаимоотношениями и связями, которые существуют и обнаруживаются у них в коллективе. Кроме того, мы знаем, что каждый ребёнок приносит в детский сад ту систему отношений, позиций и установок, которые характерны для его жизни в семье. Благодаря этому, каждая группа оказывается лишь небольшой частью более широкой системы. Ничего подобного нет в фигурах геометрии. Это, таким образом, первый существенный момент, отличающий объекты теории групп от объектов геометрии. Второй момент связан с принципами построения системы самой теории. У Евклида никогда не было единой системы фигур. Гилберту, как известно, удалось достичь такого единства, благодаря понятию абстрактного пространства. Задавая в качестве объектов точки, отрезки и плоскости, Гилберт вводит особый идеальный объект, в котором допустимы определённые преобразования элементов абстрактного пространства. За счёт этого он может всегда переходить от одной комбинации элементов к другой. Только благодаря этому появилась возможность объединить все фигуры в рамках одного объекта, но это стало возможным очень поздно. В нашем случае объект должен быть системно задан с самого начала. И эта система должна быть с самого начала предметной. Она может быть разной. Например, К. Левин называет её групповой динамикой, мы можем выделить нечто другое, но общий принцип всё равно должен быть соблюден. Это можно пояснить на более простых примерах, в частности, на примерах речи и мысли. Вот я сейчас в этой аудитории читаю вам курс лекций. А рядом, в другой аудитории, и другим человеком читается другой курс лекций, с другими словами, мыслями и понятиями. Мои лекции представляют один индивидуальный объект, а лекции другого человека — другой индивидуальный объект. Казалось бы, они никак не связаны друг с другом. Но если мы захотим исследовать и то, и другое в научной теории, то должны будем их, во-первых, связать, а во-вторых, представить особым образом, отставив в стороне всё, что касается их индивидуальности. Вы знаете, что в науке мы говорим о мышлении вообще или языке вообще. В науке мы никогда не говорим специально о тех или иных отдельных актах мышления и речи. Это не значит, что мы не описываем и не объясняем индивидуальные акты мышления и речи. Мы их описываем и объясняем, но особым образом: представляя как единичные манифестации или проявления языка как такового и мышления как такового. Но точно так же и в тех случаях, когда мы рассматриваем человеческие группы и складывающиеся в них взаимоотношения между людьми, мы изображаем и представляем их как единичные манифестации или проявления общей системы человеческих социальных отношений. Значит, мы должны анализировать единичные группы, но анализировать их таким образом, чтобы у нас предметом изучения была некоторая единая «материя» социальных взаимоотношений. А это значит, что в нашей теории групп и взаимоотношений должны быть изображены и представлены не те или иные единичные группы и не единичные ситуации взаимоотношений, а идеальная действительность групп и взаимоотношений. Два указанных момента заставляют нас с самого начала отказаться от всяких аналогий с физическими, химическими и другими естественными науками, в которых изучались отдельные объекты такого рода, какие могли быть точно представлены в теории в виде соответствующих единичных моделей. В нашем случае нужны модели совсем иного типа, модели, представляющие некоторую совсем иначе сконструированную действительность. Здесь я пропускаю целый ряд важных моментов и сразу обращаюсь к образцам исследования и описания множественных объектов, подобных нашим группам. Классическим примером теории такого типа является «Капитал» К. Маркса. В этой теории описываются буржуазные производственные отношения или то, что называется капиталом вообще, а не жизнь того или иного отдельного капитала. Мы можем надеется, что именно в работах такого типа уже были даны образцы теории, которую мы хотим построить. Анализируя их, наверное, можно было бы перенести положительный опыт и в нашу работу. Но это легче сказать, чем сделать. Теоретическая система «Капитала» дана, как известно, на определённом эмпирическом материале, она вся как бы пронизана им. Главные понятия Марксова труда: товар, деньги, прибавочная стоимость и так далее. Нам же даны люди и разнообразные взаимоотношения между ними. Поэтому непосредственно возможности переноса Марксовых схем и методов на новый материал никак не выявляются. именно поэтому мы прежде всего начинаем вести собственно методологический анализ. Чтобы переносить схемы и принципы построения исследования или научной теории с материала буржуазных производственных отношений на малые группы, надо особым образом проанализировать «Капитал» и представить заключённую в нём логику таким образом, чтобы в ней не осталось ни грана от буржуазных производственных отношений, а все было бы представлено в общих онтологических и логических характеристиках. Средствами для этого служат онтологические схемы и методологические принципы системно-структурных исследований, которые мы с вами разбирали на прошлых лекциях. Анализ рассуждений в «Капитале» и аналогичных ему трудах будет производиться таким образом, чтобы он давал проекцию на безликие системно-структурные схемы, чтобы при этом исчезало всё, что специфично для экономико-политических отношений, и оставалось лишь то, что характеризует системы и структуры вообще. Если вы помните, действуя таким образом, мы построили соответствующие модели. Прежде всего мы выделили в качестве объектов рассмотрения подструктуры, образно говоря, наиболее тесно связанных между собой элементов. Эти связи (первого рода) были изображены нами сплошными линиями. Кроме того, каждый элемент этой подструктуры был связан с другими элементами более широкой или объемлющей системы. Здесь могут быть разнообразные связи, особенно трудно описываемые и выявляемые при изучении людей и их поведения. В частности, правда, не на лекциях, а на кружковых занятиях, я специально говорил о связях, которые существуют за счёт того, что отдельный человек переходит из одних социальных систем и организаций в другие. Есть связи, которые существуют и действуют одновременно, сложно переплетаясь и взаимодействуя друг с другом. Все эти связи и зависимости между ними, обнаруживаемые нами на эмпирическом материале групп, выражаются затем в специальном структурном языке или структурной графике, разрабатываемой в общей системно-структурной методологии. Там существуют, кроме того, разнообразные понятия, которые я вводил на прошлых лекциях и сейчас не буду повторять. Нужно ещё специально отметить, что на этих же общих методологических схемах мы вводим специальные приёмы анализа систем и структур, которые, с одной стороны, развёртываются нами в плоскости самой методологии, а с другой, — проецируются на эмпирический материал групп и в их теорию. Если вы помните, здесь мы говорили опроцессах изоляции, которые противопоставлялись нами процессам абстракции, о процессах расчленения и выделения, и ещё о процессах расщепления систем. Наконец, есть ещё один момент, который был нам крайне важен. Я рассказывал о двух планах трактовки и описания того движения, которое будет осуществляться нами в собственно теоретическом слое. С одной стороны, кружки и чёрточки, представленные на структурных схемах, трактуются нами как изображения людей, их мест и связей или взаимоотношений мест и людей, а с другой стороны, они трактуются нами в плоскости методологии как элементы, связи или отношения вообще. Если, к примеру, нас спросят, что такое взаимоотношение, то мы будем отвечать, указывая на наши рабочие изображения: эти чёрточки, и ничего больше, ибо в самих явлениях группового поведения взаимоотношений и связей нет. Но точно также мы сможем, отвечая на этот вопрос, ссылаться на общие методологические схемы. При этом мы будем иметь в виду те способы и процедуры оперирования, которые фиксируются и закрепляются в собственно методологической плоскости. 51. Содержание и форма в развёртывании структурных изображений группТеперь я прошу вас обратить внимание на очень занятную сторону нашей методологической работы. Если мы хотим развёртывать теоретическую систему, описывающую группы и взаимоотношения людей в группах, то всё время вынуждены будем, оперируя с нашими рабочими схемами, спрашивать, что такое взаимоотношение, или что такое отношение, или что такое позиция человека, что такое статус его. Как и все другие исследователи, мы с вами вынуждены будем непрерывно задавать эти вопросы, вопросы, ориентированные на содержание, на выяснение того, что существует «там», в действительности и в реальности. Но, — спрашиваю я вас, — как можно на все эти вопросы ответить? И что это значит — ответить на подобные вопросы: что на деле представляют собой взаимоотношения, отношения, и тому подобное? Реплика: А что это значит — объяснить, и что, собственно, надо объяснить — черту, стрелку или Это — кульминационный вопрос наших сегодняшних занятий. Я дам на него ответ, который, наверняка, многим из вас покажется весьма парадоксальным. Ответить на вопрос, что такое взаимоотношения, причём, ответить в содержательном плане — это значит на первом этапе сформулировать правила оперирования со значками-чёрточками на наших моделях или схемах, сформулировать правила развёртывания введённых нами изображений в рамках теоретической системы. Повторяю ещё раз: сформулировать эти правила — это и значит ответить на вопрос, что такое взаимоотношения по содержанию, и единственно возможным сейчас способом. Хотя тут раздалось несколько реплик, показывающих, что мой ответ не кажется вам удивительным и что вы даже знали его заранее, тем не менее я должен признаться, что сам я с большим удивлением и недоумением отношусь к своему ответу, и до сих пор. как мне кажется, не могут его до конца осмыслить. Но всё равно, это пока — единственный ответ, который мы можем дать. Если кто-либо из вас придумает другой ответ на поставленный вопрос, то это будет здорово, и вместе с тем, это будет следующий шаг в развитии научных представлений о взаимоотношениях людей. И вклад не только в теорию человеческих групп и взаимоотношений, но и в логику и методологию научных исследований. Для тех, кто больше интересуется логическими и методологическими тонкостями построения научных предметов, я специально отмечу, что мой ответ является банальным и очевидным с точки зрения двух плоскостных схем знания и научных предметов. По сути дела, отвечая на вопрос, что такое взаимоотношения, я начинаю с формы знания и, соответственно, со знаковой формы того предмета, с которым мы с вами имеем дело. Я прежде всего указываю, с какими знаковыми объектами и каким образом мы работаем, так как полагаю, что содержание предмета и знания существует прежде всего в этом — в объектах оперирования и процедурах оперирования, что с описания их нужно начинать ответ на поставленный вопрос и что лишь затем, на следующих этапах анализа и при соответствующей онтологизации наших знаний можно будет дать другой ответ и построить другое изображение и представление взаимоотношений. Здесь, таким образом, возможны два ответа, тесно связанных друг с другом и взаимно друг друга дополняющих. На прошлых лекциях я уже касался этих вопросов, в частности, когда утверждал, что успех наших исследований во многом зависит от того, насколько нам удастся подобрать «хорошие» и «адекватные» формы знакового изображения того содержания, с которым мы здесь имеем дело. Если вы помните, я ссылался на исторические примеры развития науки, на появление алгебры, аналитической геометрии, дифференциально-интегральных исчислений и так далее. Теперь мы можем уточнить сказанное там: дело не только и не столько в знаковых средствах самих по себе, а в значительно большей мере — в способах оперирования с ними. С этой точки зрения, когда учёные и философы XVIII столетия спрашивали в то время, что такое «бесконечно малое», то по сути дела, это всегда был вопрос о том, как нужно оперировать со знаками, выражающими эти величины, чтобы получать правильные решения, хотя по форме вопрос был ориентирован на реальность, на составляющие её объекты, то есть носил онтологический характер. В этом отношении XX столетие отличается от XVIII тем, что теперь уже многие понимают, что бесконечно малые существуют не в реальности, а в нашей действительности, что они являются не объектами природы, а предметами человеческой мыслительной деятельности, что они, следовательно, существуют только в определённых моделях, и поэтому ответить на вопрос, как они существуют в реальности просто нельзя. Это — некорректный вопрос. Но точно так же и мы, чтобы задать взаимоотношения, отношения, позиции или статусы людей, мы должны, имея перед собой определённым образом организованный эмпирический материал, построить особые знаковые изображения и построить определённые процедуры работы с ними. Соответственно этому, отвечая на вопрос, что такое взаимоотношения, мы должны охарактеризовать и описать созданные таким образом предметы. И это и будет единственно возможный и единственно содержательный ответ на такого рода вопрос. Наоборот, ответ, в котором будет содержаться ссылка на какие-либо онтологические, псевдообъектные картины, будет формальным, а не содержательным, вопреки широко распространённым обыденным представлениям. 52. Три основания в развёртывании структурных изображений группВернёмся несколько назад. Как вы помните, нам нужно построить теоретическую систему. Мы с самого начала постулировали, что она будет. по меньшей мере, двухплоскостной. В ней будут, с одной стороны, выступающие в роли моделей — и нам нужно их развёртывать, — а с другой стороны, параметрические описания, которые мы получаем в Чтобы ответить на этот вопрос, мы должны обратиться к плоскости методологии, и в ней искать основания. Мы задали в этой плоскости по меньшей мере три процедуры. Прежде всего, мы должны иметь весь набор структурно-системных возможностей, мы должны знать, что может происходить со структурными объектами разных типов. На основании этого мы можем формулировать общие положения, имеющие форму методических регулятивов, отвечающих на вопрос, что, собственно, нам нужно сделать. Я могу выразить то же самое другим способом. Поскольку малые группы являются системно-структурными объектами, я могу и должен в рамках общей системно-структурной методологии рассмотреть возможные способы и формы развёртывания структур, а затем Если вы помните, мы должны ответить на все эти вопросы для того, чтобы построить единую последовательность схем, удовлетворяющих принципу выражения предельно разнообразных объектов с помощью небольшой группы единообразных схем. Таким образом, у нас оказывается три «кита», на которых покоится наше исследование. Один из них — формальные требования к любой теоретической схеме: многообразие изображений и единообразие принципов их развёртывания вместе с обеспечивающими все это понятиями из общей теории науки. Это — требование, вытекающее из принципов употребления любого современного теоретического знания, из принципов употребления его в практике развёртывания самих теоретических систем. Второй «кит» — это системно-структурная онтология, представляющая объекты совсем особого типа. Вторая группа принципов производит известное ограничение первой. Если первая относится к теоретическому описанию любых объектов, то вторая группа требований производит ограничение их, выделяя лишь системно-структурные объекты. Наконец, третий «кит», третья сторона требований и принципов выражает все то специфическое, что вытекает из особой природы малых групп и взаимоотношений людей в них. При построении своей теоретической системы мы должны удовлетворить всем трём группам принципов. Как и в предшествующих лекциях, я рассматриваю и буду рассматривать их раздельно. Это объясняется, в частности, тем, что эти группы по-разному мне известны и по-разному мной освоены. Первая и вторая — в значительно большей мере, чем третья. Поэтому, естественно, я начинаю с них и уже от них стараюсь перейти к третьей и более точно её определить. Такая последовательность, как вы без труда заметите, соответствует сформулированному мной принципу, что, приступая к изучению групп, мы должны рассмотреть, как изучалисьдругие объекты сходного типа. Но знания о том, как строятся современные научные теории и как исследуются системно-структурные объекты, и есть обобщённая форма знаний о том, как исследуются и описываются другие объекты. Иначе говоря, знания по общей теории науки и знания по системно-структурной онтологии заимствуются мной из опыта других, предшествующих исследований, а формулировка третьей группы принципов должна быть новым вкладом в науку. Не знаю, как вам, а мне очень трудно держать все эти моменты вместе и объединять их в одном рассуждении. Поэтому давайте ещё раз повторим основной принцип. Чтобы построить теорию малых групп и взаимоотношений людей, мы должны удовлетворить трём группам принципов, которые надеемся сформулировать до того, как начнётся построение самой теории. Третье и последнее из них — специфично для самой теории групп. Это — область методологии исследования групп и взаимоотношений, то есть область наших непосредственных исследований. Все это должно быть впервые открыто, этого ещё нет и поэтому оно представляет собой наиболее трудную часть. Две другие группы требований и принципов: 1) к построению научной теории вообще и 2) к построению теории системно-структурных объектов, — могут быть определены и сформулированы, исходя из уже проведённых человечеством исследований, и поэтому мы начинаем именно с них (ним), чтобы затем перейти к формулированию принципов третьей группы. 53. Общая характеристика метода восхождения от абстрактного к конкретному. Исходная структура, или «клеточка»Здесь мы должны рассмотреть широко известный и, наверняка, также известный и вам, хотя бы по названию, метод восхождения от абстрактного к конкретному. Этот метод был сконструирован впервые, По своему общему логическому смыслу этот метод аналогичен принципу и методу дедуктивно-аксиоматического построения теорий. Это есть система формальных правил для развёртывания гуманитарных теорий особого типа, подобно тому, как дедуктивно-аксиоматический метод является методом построения математических теорий особого типа. В последние 60 лет в математике развивается другой принцип и метод построения научных систем. называемый иногда конструктивным, а иногда генетическим. Первым методом, который был осознан и сознательно формулировался в науке, является дедуктивно-аксиоматический. Метод восхождения от абстрактного к конкретному является в этом плане вторым. Генетический или конструктивный метод появился третьим по порядку. Метод восхождения включает в себя прежде всего — первый его этап — задание исходной структуры целого, «клеточки». Такое название она получила у Гегеля. Каким образом задаётся клеточка — это до сих пор остаётся тайной. И в этом плане все соответствующие процедуры являются интуитивными. Единственно, что удалось, в частности А. А. Зиновьеву, анализировавшему работы Гегеля и Маркса, — это сформулировать пять признаков, которым должна удовлетворять клеточка. Имея эти признаки, можно сказать в отношении каких-либо из уже предложенных структур, являются ли они клеточками с точки зрения уже имеющегося эмпирического материала целого или нет. Но как построить клеточку для того или иного случая, и что именно должно выполнять эту роль в каждом конкретном исследовании, — на эти вопросы имеющиеся понятия о клеточке ответить не могут. Это, правда, — очень сложный вопрос. Существуют мнения, что логика вообще не отвечает на подобного рода методологические запросы, и это, в известном смысле, справедливо. Считается, что логика должна давать известные критерии, приложимые к продуктам научно-исследовательской деятельности, отвечать на вопрос, годятся ли они или не годятся для решения той или иной задачи, а находить сами эти структуры должны конкретные исследователи каждый раз в соответствии с имеющимися у них интуитивными и гипотетическими представлениями об объекте. Всех интересующихся этим вопросом я отсылаю к диссертации А. А. Зиновьева и другим более поздним работам. А мы с вами будем предполагать, что исходная структура для развёртывания или клеточка каким-то образом получилась, задана и её нужно развёртывать дальше. Это гам тем легче сделать, что у нас с вами подобная структура уже есть или во всяком случае у нас уже есть структура, которую мы хотим таким образом употреблять. А получится из этого что-либо или нет — это мы посмотрим. В принципе, наверное, любая рабочая схема, даже самая никудышная, может выполнить роль исходной схемы. 54. Процедуры восхождения как обратные аналитическимЗадав подобную структуру — а она обязательно должна быть интерпретирована эмпирически — мы обращаемся к нашему методологическому табло, и в нём ищем ответы на вопросы, что нам нужно дальше делать. Мы уже знаем, что клеточка должна дать нам возможность развернуть с помощью Попросту говоря, обращаясь к нашему эмпирическому материалу, я могу сказать, что имеющаяся у нас схема описывает самые простые случаи взаимоотношений в группах, более сложные случаи она не описывает, их должны описывать другие, более сложные структуры. Но другие структуры, которые нам нужны, должны не только описывать и изображать эти другие случаи, но они, кроме того, должны быть выведены из первой, исходной структуры, они должны быть из неё развёрнуты. Таким образом, я фиксирую два момента. Любая следующая структура в нашей теории должна быть каким-то образом развёрнута из первой структуры. С другой стороны, она должна, во-первых, соответствовать эмпирическим характеристикам, которые мы уже получили о втором объекте или о втором явлении изучаемого целого, во-вторых — служить основанием для этих характеристик, для их выведения, и таким образом объяснять их. По сути дела, эти два требования определяют всю нашу дальнейшую работу по развёртыванию теоретических схем моделей, необходимых нам для построения теоретической системы. Посмотрим, как идёт вся эта работа. На методологическом табло у нас имеются изображения систем и структур, и, в принципе, мы знаем, что можно и чего нельзя делать с изображениями такого типа как в плане отнесения их к эмпирическому материалу, так и в плане их дальнейшего усложнения и развёртывания. Очевидно, процедуры преобразования первой структуры во вторую обязательно должны соответствовать только тому, что можно делать с системами и структурами. Как вы помните, или должны помнить, мы ввели несколько процедур: изоляцию, то есть выделение Но точно таким же путём мы можем осуществить процедуры, обратные аналитическим процедурам, которые мы намечали выше. В частности, мы можем присоединять и привязывать к первой, исходной для нас структуре, не структуры, а отдельные элементы. Это будет процедура, обратная расчленению. Соответственно этому, процедурой, обратной расщеплению, будет наложение на исходную структуру Обобщая сказанное, мы можем утверждать, что если в методологии системно-структурного анализа у нас будет намечено несколько различных аналитических процедур, и весь их набор будет находится как бы перед нами, то в процессе восхождения мы будем, ориентируясь на него, выбирать те или иные обратные процедуры и в соответствии с каждой осуществлять то или иное преобразование исходной структуры. Короче говоря, восхождение от абстрактного к конкретному будет строиться нами как осуществление процедур, обратных процедурам, намеченным в методологии системно-структурного анализа. Пока мы берём все эти процедуры в рамках методологического табло, они являются формальными. Перенося их из плоскости методологии в плоскость теории групп, мы придаём им определённое предметное содержание. 55. Проблема порядка применения разных процедур как основная проблема восхожденияЗдесь, как вы уже догадываетесь, возникает целый ряд важных и существенных затруднений. Если бы в плоскости методологии была задана всего одна процедура анализа, то мы, анализируя те или иные объекты и строя их конкретные схемы, всегда знали бы. какую именно процедуру нужно применять. Но так как процедур несколько, и каждая из них играет свою существенную роль в процессе восхождения, каждая возможна и каждая нужна для описания сложного объекта, то перед нами всегда возникает вопрос, в каком порядке и в какой последовательности их нужно привлекать и применять при описании того или иного объекта изучения. Положение сильно облегчалось бы, если бы результат исследования — сложная структура, изображающая объект, — не зависел от порядка самих процедур. Но многочисленные исследовательские показали, — и с этого начинаются специфические проблемы системно-структурных исследований, — что результат в случае так называемых системных и структурных объектов самым существенным образом зависит от этого порядка: при одном мы получим одно структурное изображение, а при другом порядке — совсем иные. Это — один из самых интересных моментов описания системных исследований: при одном и том же наборе операций или процедур, комбинируя их в разном порядке, мы будем получать разные представления об объекте. Этот принцип является основополагающим для метода восхождения от абстрактного к конкретному. Можно сказать, что сам названный метод появляется тогда, когда этот принцип осознается и его начинают учитывать при определении стратегии и планов научных исследований сложных объектов. Сравнивая политэкономические работы К. Маркса и Д. Рикардо, мы видим, что успех К. Маркса в исследовании объекта был обусловлен прежде всего тем, что он нашёл иной, нежели предлагал Д. Рикардо, порядок процедур в исследовании и описании буржуазных производственных отношений. Внешне это выглядело так, что он как бы в другом порядке применял основные политэкономические категории. И именно благодаря этому, он получил иной результат. Таким образом, если на методологическом табло мы имеем ряд процедур анализа и обратных им процедур синтеза, если даже мы знаем о них всё, что нужно знать — что они собой представляют, что в результате их применения получается и так далее, — то всего этого всё равно ещё недостаточно, чтобы в плоскости теории какого-либо предмета организовать и осуществить развёртывание структурных схем и моделей. Нужно ещё знать, в каком порядке и в какой последовательности нужно все эти процедуры применять. Здесь становится очевидным, что управляющие регулятивы метода восхождения от абстрактного к конкретному не исчерпываются одними лишь формальными принципами, заимствованными из слоя методологии. Здесь приходится учитывать вторую компоненту метода восхождения от абстрактного к конкретному — его эмпирическую часть. 56. Эмпирическая составляющая метода восхождения от абстрактного к конкретномуРассмотрим более подробно, как это делается. Я уже говорил выше, что исходная схема возникает как изображение одного фиксированного нами явления, которое мы рассматриваем как простейшее явление для всего множества явлений, относимых нами к изучаемому объекту. Это значит, что эта схема служит основанием и объяснением для всего набора свойств и характеристик — а, (3, у) …, — которые были выделены при эмпирическом анализе и описании этого явления. Собственно, эта схема была так построена, чтобы объяснять эти признаки. Но, кроме того, как мы уже говорили, эта схема должна быть такой, чтобы из неё можно было развернуть следующие схемы, описывающие более сложные объекты, относимые нами к тому же предмету изучения. Это значит, другими словами, что структурные элементы, объясняющие признаки а, р1, у первого объекта или явления, должны быть одновременно опосредованными основаниями для выведения и объяснения других признаков — 8, е …, которые характеризуют более сложные явления этого же типа. Следовательно, строя исходную структуру, мы с самого начала должны знать и учитывать те эмпирические свойства, которые выявлены нами в этих более сложных явлениях. Из этого следует, что с самого начала, когда мы только ещё приступаем к развёртыванию структурных схем создаваемой нами теории, весь эмпирический материал об изучаемых нами явлениях и объектах должен быть специально организован и должен просматриваться и учитываться нами в этой его организации. Вы уже понимаете, что таким образом мы ставим перед собой новую методологическую проблему: как собирается и организуется необходимый для исследования эмпирический материал? 57. Проблема организации эмпирических данных. Генетический принцип как ключ к решению этой проблемыОна является очень сложной и трудной, может быть, самой трудной из всех методологических проблем науки. Грубо мы можем сказать, что эмпирический материал должен быть организован в ряд по принципу относительной простоты и сложности тех явлений, которые мы объединяем как относящиеся к одному предмету изучения. Это требование выводится, исходя из общих представлений о механизме самого развёртывания модели в процессе восхождения. Вы сами понимаете, что работа эта может быть только очень примерной, так как все критерии и основания для характеристики явлений как более сложных или менее сложных на первых этапах работы могут быть привнесены лишь со стороны и не могут органически вытекать из структуры объекта. Но это значит — и об этом надо всегда помнить — что подобная процедура не может дать истинных и гарантированных данных, что она всегда будет оставаться для процесса восхождения весьма произвольной и лишь, если можно так выразиться, прикидочной. Представим себе, например, что мы хотим вывести методом восхождения структуры мышления или структуры научных знаний. Мы знаем из В принципе, это очень сложное и рискованное предположение, говоря словами И. Лакатоса, — это принцип, в справедливости которого нужно сомневаться. Общеизвестно, что мышление какого-либо ординарного современного профессора Московского университета по уровню своему значительно ниже, чем мышление Аристотеля, жившего 2600 лет назад. Поэтому, ориентируясь только на хронологический принцип, мы можем получить огромное количество ошибок. Чтобы 58. «Наложение» исходной схемы на эмпирический материалПредположим далее, что какими-то способами, хуже или лучше, мы организовали эмпирический материал примерно по тем принципам, о которых выше говорили, и следовательно, эти ряды содержат монотонно усложняющиеся явления. Таким образом внизу ряда мы имеем первое явление, которому соответствует исходная структура, выше него мы имеем второе явление, которое, по предположениям, сложнее первого, ещё выше — третье, четвёртое и так далее, каждое из которых, опять-таки по предположениям, сложнее предыдущего. Мы предполагаем также, что каждое следующее явление является ближайшим по отношению к предыдущему, то есть между ними не было других обособленных явлений или, во всяком случае, если были, то разрыв, возникающий Если все эти условия выполнены, то мы как бы накладываем нашу исходную схему на второе явление. В принципе, это означает, что у второго явления должны были быть, кроме его специфических свойств 8, е и другие, также свойства первого явления — а, (3, у). В общем случае они могут быть несколько изменены и модифицированы, то есть это будут уже а’, р’, у’. Кроме того, могут быть и такие случаи, когда некоторых свойств, эафиксированных в первом явлении, во втором уже просто не будет. Такое положение дел ставит перед нами новые проблемы, но мы их будем обсуждать специально, а сейчас для упрощения оставим в стороне, то есть будем предполагать, что такого у нас нет. Кроме того, также для упрощения предположим, что первое свойство a во втором такое же, как и в первом, то есть сохраняется без всякой модификации. Рассмотрим более подробно производимое в этом случае наложение исходной схемы на второе явление. Признак a второго явления объясняется автоматически, так как он с самого начала был учтён при построении исходной структуры. Признак Р’ исходная структура непосредственно и прямо не объясняет, так как она объясняла признак 3 но вместе с тем она близка к объяснению этого признака. Сопоставляя друг с другом признаки 3 и 3’, мы можем выделить существующий между ними диссонанс. Тогда объяснению подлежит уже не само свойство Р’, а только этот диссонанс, то есть та добавка, которая вместе с признаком P образует признак Р’. Таким образом, мы производим разложение признака Р’ на две составляющие, одна из которых нами уже объяснена, а другая подлежит объяснению, причём именно для этого в исходную структуру должны быть внесены соответствующие изменения и модификации. Точно таким же образом мы поступим с признаком Y и получим, следовательно, диссонанс y в качестве нового эмпирического признака, признака второго порядка который мы будем объяснять, модифицируя исходную структуру. Признаков 8 и е в первом явлении вообще не было, поэтому их не нужно будет сводить столь непосредственным способом к их праформам в первом явлении. Это не значит, что их вообще не нужно будет сводить к Если вы помните наши предшествующие лекции, то заметите, что описанная только что процедура наложения и есть та, с которой (среди других) создаётся так называемый научный факт. Это особенно заметно на примере признаков а, Р’ и y. Не сами они, хотя и зафиксированные в качестве признаков второго явления, составляют факт, подлежащий научному объяснению. Признак a вообще выбрасывается, выводится за рамки научного факта, а от признаков Р’ и f остаются только соответствующие диссонансы, то есть в научный факт входят не сами они, а признаки второго порядка, полученные на их основе. Итак, в результате наложения схемы, изображающей первое явление в созданном нами эмпирическом ряду, на второе явление выделяются параметры, входящие в создаваемый (посредством наложения схемы на явления) факт — дис-P, дис-y, 8, е. Зафиксировав их, мы тем самым, по сути дела, определим тот набор эмпирических признаков, который необходимо иметь в виду, вырабатывая схему новой структуры. Теперь можно сформулировать более точно задачу этого шага: нужно построить такую структуру, которая служила бы основанием именно для этого набора признаков второго и первого порядка, и при этом оставалась бы основанием для всех уже учтённых и неявно выраженных в ней признаков. Если бы второе явление было таким, что в нём, скажем, совершенно отсутствовал бы признак y или у7, то задача работы, естественно, несколько бы изменилась. В этом случае мы должны были бы создавать такую структуру, которая, благодаря ли потере Я хотел бы специально отметить, что, конечно, более конкретный анализ всех процедур, которые здесь нужно осуществить, предполагает более конкретное и детализированное описание самих свойств, в частности, детальную характеристику их типов. Если свойства будут функциональными, то понадобятся иные процедуры разложения и сведения, а также иные структуры для их объяснения, чем в тех случаях, когда эти свойства будут атрибутивными или относительными. Но все эти вопросы не могут обсуждаться сейчас, в контексте этих лекций, так как они нуждаются в значительно более глубоком логическом анализе, чем тот который мы можем провести сейчас. Я, таким образом, лишь указываю на весь этот круг вопросов, оставляя его анализ до другого времени. 59. Построение второй структуры путём развёртывания первойКогда сведение признаков второго порядка к признакам первого и изображающей его структуре произведено, когда, таким образом, конкретно поставлена задача для дальнейшего развёртывания исходной структуры, тогда, собственно, и начинается самое главное в процессе восхождения от абстрактного к конкретному. Именно этой процедуры или этой части исследования касаются его специфические принципы: они задают особый способ синтеза структур или, другими словами, особый способ перехода от исходной структуры к следующей. Чтобы разобрать и описать его, мы должны вновь обратиться к методологической плоскости нашей работы. Чтобы пояснить суть этих признаков, рассмотрим прежде обратные восхождению процедуры разложения структур. Пусть (см. 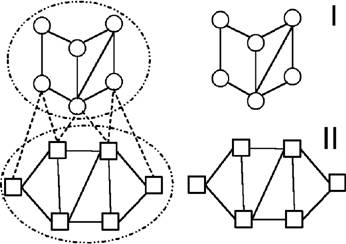схему 26) нам дана достаточно сложная структура обобщённого массового предмета. Для простоты будем предполагать, что в ней не существует принципиальных различий между связями, соответствующими отдельным объектам-явлениям, и связями, соответствующими организации этих объектов в один предмет. Ясно — и это легко увидеть на схеме, — что мы можем в заданном структурном объекте выделить сначала подструктуру I, а затем, независимо от проделанного выделения, выделить ещё подструктуру II.
Если это будет сделано, то мы получим как бы два независимых изображения их, взятых отдельно друг от друга, а затем сможем ставить вопрос о том, как они связаны друг с другом и как друг к другу относятся. Отвечая на этот вопрос, мы будем осуществлять синтез — процедуру, обратную произведённому нами разложению. Все традиционные гносеологические и логические постановки вопроса об анализе, синтезе и их отношении друг к другу исходят из представления именно о такой процедуре разложения и именно такой постановки вопроса об обратном объединении их результатов — выделенных нами подструктур. Точно так же можно сказать, что традиционные способы анализа и синтеза исходят из того, что с любым объектом можно проделать подобную вещь, то есть подобное разложение, и что затем можно будет соединить полученные подструктуры I и II, и таким путём воспроизвести то, что было реально дано в самой исходной структуре. Вы не должны здесь забывать, что в плоскости теории предмета эти структуры даны и всегда употребляются не сами по себе, а в сопровождении определённых эмпирических характеристик объектов, и что обязательно процедурам разложения и объединения структур должны соответствовать Ещё более схематизируя и обобщая рассматриваемую ситуацию, мы можем сказать, следовательно, что в отношении любого объекта О существует процедура выделения в нём свойств-сторон А, В, С и так далее, что каждое из этих свойств мы можем выделить независимо от выделения других сторон, в любом порядке, и что затем мы можем соединить эти характеристики союзом «и», и таким путём из многих односторонних знаний получим одно многостороннее знание об объекте. Таковы принципы Аристотелевой логики, в соответствии с которой построены как наша обычная речевая коммуникация, так и научный анализ и описание объектов. Во всяком случае, так оно было построено до появления метода восхождения от абстрактного к конкретному. Суть метода восхождения от абстрактного к конкретному состоит прежде всего в том. что отвергается всеобщность подобных процедур синтеза и соответствующих им процедур анализа. Кроме того, выделяется особый класс объектов, называемых системно-структурными, к которым подобные метода анализа и синтеза уже не приложимы, и которые, следовательно, нуждаются в иных методах. Короче говоря, утверждается, что системно-структурные объекты не могут быть проанализированы и описаны на основе таких методов. Для них нужен принципиально иной метод. Представители немецкой классической философии — Фихте, Шеллинг, Гегель, Маркс — констатируют и описывают его. Идея этого метода состоит в том, что в сложной структуре на первом шаге может быть выделена особая подструктура, которая и будет зафиксирована в первом исходном изображении объекта.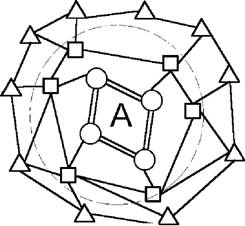
Эта структура не может быть любой, а должна обладать строго определёнными свойствами. Они были зафиксированы в определении исходной структуры как «клеточки», и выше мы их уже в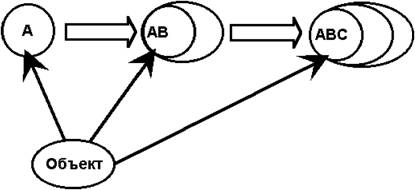
Создатели этого метода говорили, что подструктура В должна быть объединена с исходной структурой А органическим путем. Они формулировали правила, позволяющие осуществить такое объединение структур. Фактически это был не синтез или объединение двух подструктур, а преобразование исходной структуры А в новую более сложную структуру АВ. Если при Аристотелевом способе разложения объектов и построения знаний о них каждое из свойств сторон особым образом характеризовала объект, и каждое было нужно отдельно от других: появление характеристик В и С не делало не нужным А, точно также, как А не делало не нужным В и С, то при восхождении от абстрактного к конкретному второе структурное изображение АВ делает уже ненужным прежнее структурное изображение А. По сути дела, новая структура АВ такова, что она не может быть разложена на две подструктуры — А и ещё какую-то, она представляет собой единую, органическую, то есть неразложимую механически на две части структуру. Именно это обстоятельство фиксируется мной в наглядной форме в том способе, каким я записываю саму букву, обозначающую эту новую структуру: это — такая же единая, как буква А, в ней нет двух отдельных целостных составляющих, она не может быть разложена на две части, которые имели бы самостоятельное, независимое друг от друга значение и смысл; хотя из второй структуры может быть выделена одна целостная и независимая подструктура А, то, что останется после этого, не будет иметь никакого смысла и значения. Именно это главный момент в методе восхождения от абстрактного к конкретному. Как вы уже, наверное, догадываетесь, он совершенно Характеризуя отношение между первой и второй структурами, говорят обычно, что вторая снимает в себе первую (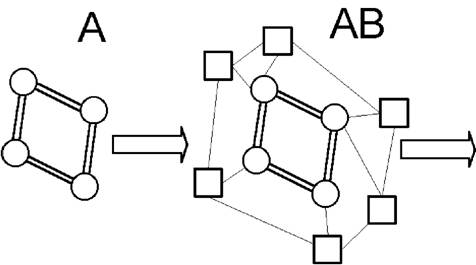схема 29).
Из всего сказанного следует, что в качестве второй структуры мы должны задать такое образование, которое бы содержало в себе всё, что содержалось в первой структуре и ещё, кроме того, 60. Проблема трансформации исходной структуры в окружении второй структуры. Организация и организованностиНо здесь, как мы с вами сейчас увидим, возникают большие и трудно преодолимые затруднения. Когда мы берём один выбор элементов и связей и представляем их в виде относительно целостной подструктуры А, а затем берём тот же самый набор элементов и связей, но теперь уже как элементы и связи новой структуры, то при этом — таковы требования общего понятия о структуре — должны измениться и меняются все элементы и связи, входящие в состав подструктуры А. Вы ведь помните, что структурой в отличие от организованности, мы называем только то, в чём элементы и связи зависят друг от друга, а следовательно, меняются каждый раз, когда мы добавляем к ним Именно это обстоятельство создаёт основные методологические затруднения, именно оно составляет суть основных методологических проблем, и вместе с тем, в нём заключена основная особенность метода восхождения: будущие изменения или модификации элементов и связей клеточки при развёртывании её в более сложные структуры должны быть учтены каким-то образом с самого начала, то есть тогда, когда мы ещё только приступаем к построению самой клеточки и вводим первые предположения о принципах её дальнейшего разложения. Другими словами, основная методологическая трудность восхождения от абстрактного к конкретному состоит в том, чтобы каким-то образом учесть те изменения в элементах и связях исходной структуры, которые обязательно должны произойти, когда мы соединим их с другими элементами и связями и таким образом перейдём от исходной структуры к новой, более развитой. Если, скажем, каждый элемент исходной структуры имел определённые свойства-функции, то мы должны иметь метод в соответствии с которым, прибавляя к примеру элементы е, к …, мы сможем сказать, во что превратятся исходные свойства-функции всех элементов. Значит, наша задача состоит в том, чтобы не только дополнить исходную структуру новыми элементами и связями, но в ещё большей степени в том, чтобы сформулировать правила и законы изменения свойств-функций в ходе тех или иных развёртываний структур. Надо сказать, что эти задачи настолько сложны, что обычно их не решают, а сводят к другим, более простым. Этот путь достаточно эффективен, если мы имеем дело с проектированием. В этом случае структурные связи подменяются организационными, а на сами исходные структуры тем самым накладывается требование, чтобы их элементы и принадлежащие элементам свойства-функции оставались неизменными при дополнении системы или преобразовании её в более сложную. Существенно также, что первые примеры восхождения были построены, по сути дела, не на материале структур, а на материале организованностей. Товар и товарное отношение есть организованность особого вида, а не структура. Здесь особым очень существенным приёмом является образование связок из синтагматических и парадигматических систем. Этот приём используется нами не только при исследовании и описании речи-языка, но при исследовании всех других социальных объектов. Синтагматическая система является структурой в полном и точном смысле этого слова, а парадигматическая, напротив, — организованностью. За счёт общности их элементов мы получаем возможность переводить структуру в организованность, а затем от организованности переходить назад к структуре. Это — всеобщий приём мышления: числовой ряд тоже построен на том, что количество переводилось там в порядок, количество выражалось через порядок, а порядок служил формой выражения количества. Слово «дом» в предложении «Дом стоит на горе» и в другом предложении «Дома являются сооружениями» — это разные слова, но за счёт того, что существует парадигматическая система организации слов языка, мы воспринимаем и рассматриваем его как одно слово в разных контекстах. Соответственно этому мы всегда знаем языковой. лексический смысл этого слова, и, кроме того, всегда интуитивно выделяем специфический смысл, образованный тем или иным контекстом. Происходит как бы автоматическое разложение каждого слова в предложении на слово-эталон из парадигматической системы языка за счёт того, что мы относим слово из предложения к этой парадигматической системе, и добавку, возникающую благодаря предложению и тому целостному смыслу, которое оно выражает. Таким образом, элемент синтагматической структуры сводится к элементу организованности, и, кроме того, ещё учитывается в специфических структурных добавках. Те же самые проблемы встают перед нами в изучении малых групп. Любой элемент системы группы остаётся тем же самым, переходя в другие группы, или же тогда, когда изменяется конфигурация группы. Вместе с тем, в каждом из названных случаев он получает дополнительные свойства-функции. И это не только исследовательский приём. Реально человек, в частности ребёнок, остаётся тем же самым, переходя в новое окружение, и вместе с тем, он всегда меняется, как бы в отсветах этого окружения. Казалось бы одна игра, но в ситуации, когда сначала нет педагога, а потом он, к примеру, приходит и становится у двери, это во многом разные игры и разные системы. Но всё равно элементы той и другой мы должны рассматривать как сохраняющиеся, как непрерывные. Это должно быть ясно всем, кто хоть сколько-нибудь размышлял над человеческими взаимоотношениями. 61. Эмпирический материал и правила формального развёртывания структурНо вернёмся к основной теме нашего обсуждения. Как вы помните, мы должны теперь ввести такую структуру, исходя из первой исходной, чтобы она охватывала все свойства, включённые нами в факт, построенный на основе сопоставления второго и первого явления. При этом каждый переход, осуществляемый нами, требует анализа и объяснения. Одни из этих переходов с точки зрения объекта кажутся более естественными и очевидными, другие, наоборот, — более сложными и наводящими на размышление. В частности, нас не удивляет то обстоятельство, что с переходом ко второму явлению свойство → превратилось в свойство → →. Так собственно и должно быть, поскольку идёт речь о превращении одной структуры в другую. Но свойство → П не претерпело такого изменения, и это заставляет ставить вопрос о том, почему этого не произошло, в чём особенности соответствующего превращения и наших процедур конструирования, отражающих его. По сути дела, здесь мы должны объяснить, почему Вы должны также иметь в виду и помнить, что исчезновение Сделаем здесь скачок дальше. Предположим, что мы построили вторую структуру. На что мы при этом ориентировались? Очевидно, прежде всего на созданный нами факт и составляющие его элементы-свойства. Но этого ещё мало, и это даже не главное. Вы помните, что нам нужно построить систему теории, а для этого задать процедуры развёртывания схем-моделей. Восхождение от абстрактного к конкретному есть вид формально-дедуктивного построения. А это значит, что оно не может ориентироваться на одни лишь факты и исходить только из них. Нужна В результате одного лишь перехода от первой структуры ко второй трудно получить достаточно хорошую, подходящую для данной эмпирической области процедуру, хотя, в принципе, она выявляется на материале двух структур, и ничего другого для неё не нужно. Но таким образом получается какое-то правило, а нам нужно правило наиболее точное для данной, обычно очень широкой области эмпирического материала. Поэтому даже получив подобное правило из двух случаев. мы продолжаем работу, подыскивая наиболее точное и адекватное правило. Для этого мы накладываем вторую структуру на третье явление из организованного нами ряда эмпирического материала, и таким путём создаём новый, третий факт. Отличием работы на этом этапе от процедур на предыдущих этапах является то, что мы можем, исходя из уже сформулированной нами процедуры, развернуть вторую структуру в третью чисто формально и таким образом получить теоретической объяснение третьего факта, совершенно не учитывая самих фактических данных. Тогда у нас получится сразу две структуры, относимых к третьему факту: вторая, к которой нужно сводить третье явление, и третья, которая получена из второй путём формального развёртывания и, вместе с тем, должна объяснять третье явление. Можно сказать, что здесь получается два факта: один — благодаря сведению третьего явления ко второй структуре, а другой — благодаря соотнесению третьего явления с третьей, формально полученной структурой. Это, естественно, расширяет наши комбинаторные возможности и создаёт дополнительные определения самой задачи и наших исследовательских процедур. В специальном обсуждении здесь нуждается вопрос о том, как мы получаем знание о нашей процедуре развёртывания схем и формулируем формальное правило. Из всего того, что мы с вами уже знаем, следует, что здесь обычно прибегают к рефлексивному анализу процедур своей собственной работы (в определённом аспекта я обсуждал эту проблему в статье в сборнике «Педагогика и логика» [Щедровицкий, 1968 а], когда рассматривал процедуру построения моделей изменения и развития). Сложности обычно возникают потому, что возможности развёртывания схем весьма разнообразны. Нам всё время приходится определять более точный и более правильный порядок осуществления разных процедур перехода от более простых структур к более сложным. Именно здесь эмпирический материал играет определяющую роль при условии, что формальные возможности развёртывания нами уже Тогда, по сути дела, целью нашего анализа оказывается уже метазадача: сначала мы определяли возможные процедуры формального развёртывания схем, и их оказалось несколько разных, их нужно комбинировать, и поэтому мы определяем ещё одно правило, касающееся их комбинирования, и оно выступает как результат и средство второго порядка. Здесь происходит раздвоение задач и направлений исследований: конструирование математик (эмпирическое по-своему происхождению) отделяется от собственно эмпирического исследования данного объекта. Поэтому мы никогда не сможем освободиться от ориентировки на эмпирический материал и необходимости учитывать его, хотя нередко мы будем исправлять этот эмпирический материал в соответствии с возможностями конструктивного и формально-дедуктивного представления объекта. Мы никогда не сможем строить теорию объекта чисто формальным путём, отбрасывая эмпирический материал, но мы таким образом будем строить теоретические системы, и они будут системами математики, Поэтому построение теории объекта никогда не может быть чисто дедуктивным, а всегда должно быть дедуктивно-эмпирическим. Специфический признак теоретической системы состоит как в том, что мы выделяем формальные процедуры развёртывания схем, так и в том, что мы постоянно ориентируемся на них, рассматривая их как столь же существенный фактор, что и эмпирический материал, а совсем не в том, чтобы отказаться от эмпирического материала или не признавать за ним существенную роль. Здесь мы сталкиваемся с очень важной и существенной проблемой, касающейся определения веса и роли каждого из этих факторов в том или ином случае. Если в ходе подобных исследований нам приходится? с одной стороны, исходя из эмпирического материала, определять формальные процедуры развёртывания схем, а с другой стороны, учитывая уже выявленные формальные процедуры, определить порядок осуществления их в соответствии выявляемым эмпирическим материалом и при этом вносить коррективы в сам эмпирический материал, то вся работа становится достаточно неопределённой и динамической. Мы никогда не знаем, какую из этих позиций выгоднее и целесообразнее принять в каждом отдельном случае. Мы не знаем, что нужно делать: исправлять формальную систему в соответствии с эмпирическим материалом или, наоборот, расчленять и разлагать эмпирический материал, приводя его в соответствие с формальными алгоритмами и процедурами развёртывания моделей. Нам каждый раз приходится определять вес и ценность того и другого, отдавая предпочтение одному в ущерб другому. В зависимости от веса, который мы приписываем эмпирическому материалу или, наоборот, формальным процедурам, мы получаем одни или другие результаты нашего теоретического исследования. Но такова общая судьба всякой научной работы, и нам не приходится по этому поводу горевать. Нам важно другое — отчётливо представить себе специфические моменты восхождения от абстрактного к конкретному как одной из процедур построения системы теории сложных объектов. |
|||||||||||||
