Георгий Петрович Щедровицкий:
Избранные труды.
Часть VII. Развитие. Учение. Игра. К анализу процессов решения задач

I

Проводимая в настоящее время перестройка школы поставила перед педагогической наукой целый ряд новых исключительно важных задач. Одной из них является задача коренного улучшения методов обучения и воспитания детей.

Важность её определяется, в частности, тем, что учебная программа новой школы, предусматривающая сочетание политехнических дисциплин с производительным трудом при сохранении гуманитарного образования, неизбежно связана с увеличением материала, подлежащего усвоению. Вместе с тем хорошо известно, что уже при прежней программе наблюдалась перегрузка школьников учебными занятиями. Вопрос о необходимости сужения программы не раз поднимался в нашей печати, но опыт показал, что ни один из существующих предметов не может быть выброшен или существенно сокращён. Теперь же к ним прибавились ещё новые предметы.

Решение этого важного вопроса может заключаться только в изменении характера самого учебного процесса, в предельной рационализации его.

В качестве средства такой рационализации выдвигают дифференциацию и специализацию обучения на втором этапе образования. Это, без сомнения, правильная и вполне назревшая мера. Однако не менее важным и назревшим является переход к «активным» методам обучения и воспитания, которые позволили бы учащимся в более короткие сроки и с меньшими усилиями овладеть необходимыми знаниями и умениями. Это, на наш взгляд, является главным средством рационализации учебного процесса.

Одной из причин, почему существующие методы обучения приводят к перегрузке учащихся, является то, что они пока ещё плохо используют скрытые возможности развития умственных способностей детей. Известно, что быстрое и прочное усвоение знаний, умение быстро найти правильное решение в новой производственной или жизненной обстановке во многом зависят от правильного воспитания внимания, памяти и, в особенности, мышления учащихся. Но существующие методы обучения почти не обеспечивают сознательной и систематической работы учителя по формированию этих психических деятельностей. При существующей практике обучения они складываются, как правило, стихийно. Новые методы, напротив, должны быть рассчитаны прежде всего на воспитание способностей учащихся, причём особое внимание при этом должно быть обращено на формирование у учащихся навыков самостоятельного умственного труда, умения самостоятельно планировать свою работу, анализировать её состав, намечать этапы и тому подобное.

II

В школе одним из главных средств воспитания мыслительных способностей учащихся является решение учебных задач. В настоящее время при построении отдельных учебных задач и определении порядка их расположения в учебниках и задачниках учитывают в основном только предметное содержание этих задач и усложнение содержания и, как правило, не учитывают сложности тех действий, которые учащийся должен проделать, чтобы решить задачу. Между тем главным фактором, определяющим развитие мыслительных способностей в ходе решения задач, являются именно характер и структура той мыслительной деятельности, которую осуществляет учащийся, и последовательность усложнения этой деятельности в ходе обучения. Поэтому для построения рациональной системы обучения, формирующей у учащихся мыслительные способности, необходимо осуществить широкий круг логических и психологических исследований структуры мыслительной деятельности, а также условий и закономерностей её формирования. В частности, необходимо проанализировать с точки зрения состава и структуры деятельности процессы решения разнообразных практически-познавательных задач и дать основанную на результатах этого анализа классификацию учебных задач.

III

Подобно всем другим мыслительным процессам, процессы решения задач могут рассматриваться в двух хотя и тесным образом связанных друге другом, но тем не менее существенно различных планах:

• А. По своему объективному составу и структуре, которые только и могут обеспечить решение данной задачи и в этом отношении не зависят от субъективных средств отдельных индивидов; в этом плане мыслительный процесс решения задачи рассматривается как «трудовая норма».
• Б. С точки зрения тех действий, которые могут и должны осуществить индивиды, чтобы, исходя из определённых знаний и навыков деятельности, в той или иной форме овладеть новым составом деятельности, новой «нормой»; действия второго плана определяют тот субъективный способ, каким отдельные индивиды в дальнейшем будут осуществлять трудовую мыслительную деятельность.

В настоящем сообщении мы будем рассматривать процессы решения задач только в первом плане — как «норму». Такой анализ является предварительным условием развёртывания исследований процессов решения задач во втором плане; действительно, чтобы исследовать формирование каких-то знаний или мыслительных операций в онтогенезе, надо предварительно выяснить, что при этом формируется, что представляют собой уже сложившиеся, готовые знания и мыслительные операции. Мы исключим также практические действия и ограничимся процессами решения познавательных задач.

IV

Решение всякой познавательной задачи является определённым мыслительным процессом. Поэтому исследование процессов решения задач во многих отношениях фактически совпадает с исследованием мыслительных процессов. Суть мыслительной деятельности, с нашей точки зрения [1957 b, с. 42; 1958 b*, I, (с. 590–592); 1960 с*, I, (с. 1–3)], заключается в замещении исследуемых объектов другими объектами (эталонами и «посредниками») или знаками. Поэтому процессы решения задач правильнее всего классифицировать в соответствии с тем, чем в ходе решения замещается исследуемый объект и как он замещается.

На первом этапе анализа в этом направлении оказалось целесообразным подразделить все процессы решения задач на четыре основные группы:

1.

Для характеристики первой группы можно взять мыслительные операции, которые мы осуществляем, отвечая на вопросы: «Сколько предметов на этом столе?», «Какова длина этого стола?», «Равны ли по длине эти две верёвки?» и тому подобное. Во всех этих случаях исследуемый объект (обозначим его знаком X) и вопрос относительно него заданы таким образом, что существует одна познавательная операция — счёт, измерение, наложение и тому подобное (обозначим их знаком А, читай «дельта»), — решающая задачу. Эта познавательная операция направлена непосредственно на объекты (и сама представляет собой особую модификацию замещения одних объектов другими), она выделяет в объектах определённое содержание и может рассматриваться как лежащая в одной плоскости с самими объектами (см. [1958 b*, V, (с. 618–620); 1960 с*, I, (с. 1–3)]). Результат этой познавательной операции — определённое языковое выражение или знаковая форма (цифры, слова «равно» и «не равно» и тому подобное) находится уже как бы в другой плоскости по отношению к объектам и самой операции: операция как бы исчезает и в этом языковом выражении, последнее замещает операцию и выделенное посредством неё содержание. Наглядно-схематически описанный процесс решения задачи может быть изображён формулой ХΔ↑^(А), где вертикальная стрелка ↑ обозначает переход от объективного содержания, выявленного в плоскости объектов, к знаковой форме, лежащей уже в другой, более «высокой» плоскости.

2.

В ряде случаев объект и вопрос относительно него бывают заданы таким образом, что не существует одной познавательной операции, посредством которой можно было бы непосредственно решить задачу. Например, нельзя непосредственно сопоставить по длине два непередвигаемых объекта, расположенных в разных местах; нельзя измерить длину кривой линии прямолинейным эталоном и тому подобное. В этих случаях задачу решают, преобразуя исходный объект X к такому виду Y или замещая объект X другим объектом Y, таким, что к Y может быть применена какая-либо операция типа Δ, дающая знание, которое может рассматриваться как ответ на вопрос относительно X. При этом между X и Y устанавливается особое отношение замещения, которое получило название отношения эквивалентности [Ладенко, 1958 а]. Именно таким образом, к примеру, решал задачу Галилей, когда он приступил к изучению свободного падения тел, но не мог достаточно точно измерять время такого движения и заместил его движением шарика, скатывающегося по наклонной плоскости (см. [1958 а*]). Наглядно-схематически описанный процесс решения задачи может быть изображён формулой X = YΔ↑^(А), где знак = (читай «эквивалентно») обозначает замещение исследуемого объекта X другим объектом Y. Для этого процесса характерно то, что как операция замещения, так и познавательная операция А осуществляются в плоскости объектов, а языковое выражение [А], фиксирующее содержание, выделенное посредством Δ в объекте Y, относится к объекту X (см. [Ладенко, 1958 а, с. 70]).

3.

В качестве примера процессов третьей группы можно взять определение вида вещества в соответствии с положением «Если вещество окрашивает лакмус в красный цвет, то это вещество есть кислота». Необходимым условием процессов этого вида являются предварительная выработка и использование в ходе самого решения задачи сложной знаковой формы (иначе — формального знания), которая в простейших случаях представляет собой отдельное выражение вида «Все [В] суть [А]» или систему таких выражений. В специальной серии сообщений [1958 b*] мы разобрали условия и закономерности формирования знаковых форм такого вида, относящихся к категории атрибутивного знания, и дали общую схему решений, основанных на использовании этих форм (см. [1958 b*, V]). Наглядно-символически эти процессы решения задач можно изобразить в формуле XΔ↑^(B)λ(A), где [В] есть знаковое выражение, фиксирующее результат применения операции Δ к объекту X, а λ изображает «формальные преобразования» (осуществляемые в соответствии со связями и правилами формальной знаковой системы), приводящие выражения вида [В], (С), (О)… к виду [А], которое может рассматриваться как ответ на исходный вопрос относительно объекта X. В простейших случаях, когда знаковые системы имеют вид «Все [В] суть [А]», эти преобразования представляют собой просто переход по связи от [В] к [А] и приписывание объекту X свойства, зафиксированного в выражении [А], — процесс решения задачи может быть изображён в этом случае формулой ХΔ↑^{(B) → (A)}, — но в более сложных случаях эти преобразования включают в себя собственно формальные действия — «присоединение», «исключение» и тому подобное (см. [1958 b*, V; (с. 617–618)]).

Другими примерами процессов этой же группы будут: сложение нескольких чисел, дающее ответ на вопрос о количестве объектов в совокупности, части которой находятся в разных местах; вычисление длины окружности на основании формулы l = 2πr, после того как измерена длина радиуса этой окружности; использование уравнения химической реакции для ответа на вопрос, какие вещества получатся, если мы приведём во взаимодействие другие определённые вещества, и тому подобное. Генетически все эти процессы значительно сложнее, чем процессы, основывающиеся на знаковой форме атрибутивного вида, и, в частности, возникают как сокращения комбинаций из процессов решения вида 2 и 3, но с функционарной точки зрения, то есть с точки зрения способа непосредственного осуществления, они ничем принципиально не отличаются от процессов, разобранных выше. Для всех процессов этой группы характерно, что большая часть составляющей их деятельности лежит в плоскости знаковой формы (есть, следовательно, деятельность не с объектами, а со знаковыми выражениями) и имеет чисто формальный характер.

4.

К четвёртой группе мы относим все те случаи, когда объект и вопрос относительно него заданы таким образом, что для решения задачи нужно осуществить сложную комбинацию замещений исходного объекта различными знаковыми формами (часто также и одних знаковых форм другими) и преобразований (формальных и содержательных) этих знаковых форм, то есть процессы, представляющие собой комбинации процессов вида 2 и 3.

Характерными примерами процессов такого вида являются решения геометрических задач. Важно специально отметить, что на определённых этапах решения этих задач знаковые формы, замещающие исходный объект, рассматриваются как объекты особого рода и к ним применяется особая деятельность, напоминающая содержательные преобразования собственно объектов, рассмотренные под п. 2. Специфику подобных процессов решения задач составляют каждый раз порядок и способы комбинирования элементарных процессов вида 2 и 3. Соответственно мы получаем для изображения этих процессов решения задач различные формулы.

Например, процесс решения геометрической задачи, при котором исходная фигура включается в более сложную фигуру и получает в связи с этим новые определения, позволяющие в соответствии с уже имеющейся сложной знаковой формой приписать этой фигуре (а вместе с тем и объекту X) новое свойство, может быть изображён в формуле: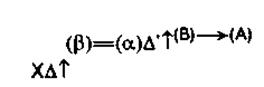

Где [β] есть геометрическая фигура, замещающая на основе операции Δ исходный объект, (α) — эта же фигура, получившая новое определение, = — знак эквивалентного замещения, Δ’ — операция, выделяющая в [α] свойство, которое фиксируется в знаке [В], а [А] — знаковое выражение свойства, которое в соответствии с формальным знанием [В] — (А) приписывается [α], затем [β] и, наконец, самому X. Важно также отметить, что часто повторяющиеся комбинации элементарных процессов закрепляются в виде определённых строго фиксированных приёмов; в качестве примера можно указать на приём среднего пропорционального в геометрии.

5

Необходимым условием решения задач вида 2, 3 и 4 являются умения оперировать (содержательно и формально) со знаковой формой. Эти способы оперирования нередко бывают очень сложными; они, как правило, отделяются от тех задач, для решения которых возникли, и выделяются в особые научно-теоретические задачи. Геометрия, например, возникла из оперирования с вещами окружающего мира и для решения сугубо практических задач, но как наука она имеет дело исключительно с чертежами фигур и другими знаками и отвечает на вопросы, поставленные относительно них; подобно этому арифметика имеет дело только с числами, алгебра — с величинами, выраженными в буквах, и тому подобное. По отношению к исходным эти новые задачи являются вспомогательными, вторичными, или, как говорят, задачами других, «более высоких» уровней. Они имеют смысл и значение лишь как средства решения исходных задач, но это не мешает им обособляться и существовать относительно самостоятельно в виде структур, соответствующих перечисленным выше. Таким образом, складывается сложная иерархия относительно самостоятельных и в то же время тесно связанных друг с другом познавательных задач и способов их решения (см. [Ладенко, 1958 b; 1959]). Важно специально отметить, что конкретный анализ различных уровней этой системы даёт, по-видимому, возможность классифицировать и все разнообразные виды знаковых форм и действий с ними в соответствии с тем местом, которое они занимают в этой иерархии задач.

6

Изложенные выше соображения позволяют сделать важный дидактический вывод. Если мы ставим задачу обеспечить формирование у учащихся необходимого комплекса мыслительных способностей, то система учебных задач должна строиться в соответствии с изложенными выше принципами иерархии: она должна отражать как относительную самостоятельность каждой познавательной задачи, так и их тесную связь и зависимость друг от друга. В частности, задачи этой системы должны располагаться в последовательности, соответствующей сложности процессов их решения. Сами процессы решения каждой задачи должны: а) вводиться как средство и условие решения другой задачи, нижележащего уровня; б) отрабатываться как процесс решения особой задачи, безотносительно к задаче нижележащего уровня, в) включаться как особый целостный процесс в решение задачи нижележащего уровня. Только такой порядок отработки учебных задач может обеспечить сознательное усвоение способов их решения и формирование соответствующих мыслительных способностей.