Георгий Петрович Щедровицкий:
Избранные труды.
Часть VI. Понятие. Знание. Модель. О некоторых моментах в развитии понятий

Одна из наиболее важных задач диалектико-материалистической логики состоит в исследовании процессов развития понятий. Эта задача выходит за рамки так называемого формально-логического подхода к мышлению, не рассматривающего процессы образования знаний.

В ходе общественной практики люди открывают в предметах и явлениях действительности все новые и новые свойства и отражают их в мысли. Эти отражённые свойства предметов и явлений объективного мира составляют содержание нашего знания, содержание наших понятий. Реальные процессы, тела или явления, которые исследуются и о которых образуются те или иные понятия, составляют объект мысли. Содержание понятий никогда не исчерпывает всех свойств объектов, оставаясь всегда относительно ограниченным и односторонним.

Следуя за развитием общественной практики, оно постоянно меняется, а вслед за изменением содержания понятий меняется их строение.

Изменение строения понятий проявляется в их языковом выражении. Понятие может быть выражено отдельным словом (стол, дом, энергия, желтый и другие), предложением (кислота содержит водород), формулой (y = f [х₁ х₂ х₃…]) или целой системой связанных между собой предложений, как, например, понятие о буржуазных производственных отношениях, представленное в трёх томах «Капитала» К. Маркса, и других. Языковое выражение понятия составляет его форму. Форма имеет своё строение, которое входит в характеристику строения понятия в целом. Более подробно все эти определения — формы, строения понятий и тому подобное — разобраны в наших статьях [1957 а*; 1958 b*, l].

Строения понятия, в частности строение его формы, определяются, во-первых, характером объекта мысли и, во-вторых, «глубиной» познания, «глубиной» проникновения в объект. Последнее, в свою очередь, определяется характером познавательной деятельности, в частности характером и степенью опосредствования исследуемого отношения другими отношениями в процессе познания.

На примере механического понятия скорости мы попробуем наметить некоторые, на наш взгляд, общие моменты в развитии строения понятий.

***

Первое простейшее понятие скорости выражалось в форме отдельного слова: скоро, скорее. (Мы оставляем в стороне вопрос о том, как образовалась эта абстракция, что послужило толчком к её образованию и как было найдено слово.) Сравним содержание этого понятия с содержанием обобщённого понятия движение ¹ (или с частными понятиями движения — бежит, летит и тому подобное) У них один и тот же объект, то есть они отражают одно и то же свойство предметов объективного мира, но отражают его по-разному.

Образование абстракции движение предполагает сопоставление двух тел. (Мы оставляем в стороне вопрос об устройстве органов зрения и рассматриваем здесь лишь отношения между объектами, необходимые для сопоставления при образовании какой-либо абстракции.) Одно из этих тел — обычно земля с расположенными на ней предметами — принимается за неподвижное и служит «телом отсчёта», относительно которого рассматривается движение другого тела. При этом абстракция движение выступает как обозначение атрибутивного свойства второго тела. Но фактически она обозначает изменение пространственного взаимоотношения между этими двумя телами.

Образование абстракции скоро, скорее предполагает сопоставление по крайней мере трех предметов: земли и двух движущихся относительно неё тел. Отношение каждого из них к земле уже фиксировано, отражено в понятии движущееся. Сравнение уже зафиксированных в абстракции движений есть сравнение отношений. Однако первоначально оно осознается как сравнение двух движущихся предметов. Без третьего тела, относительно которого рассматриваются два других, никакое чувственное сопоставление движений невозможно. Первоначально это третье — земля или место — выступало как нечто случайное по отношению к самим движениям и к процессу их сопоставления. Сегодня это было одно место, завтра другое, послезавтра третье. Поэтому, хотя оно и всегда участвовало в процессе сопоставления движений, его участие в образовании абстракции скорости длительное время не фиксировалось, не осознавалось.

Абстракция движения, выраженная отдельным словом, имела смысл и значение независимо от той или иной реальной ситуации и её чувственного отражения, если само слово движение имело фиксированный и общезначимый смысл. Абстракция скоро, скорее вне определённой, непосредственно воспринимаемой конкретной ситуации, вне её чувственного отражения не имела никакого смысла, хотя значение самого слова скоро могло быть фиксировано и, следовательно, общезначимо. Говоря, что предмет А движется скорее или скоро, мы всегда должны иметь в виду другой предмет, В, который воспринимается в этот момент точно так же непосредственно и движется медленнее предмета А ².

Понятия такого вида, то есть не имеющие определённого смысла вне известного чувственного восприятия, а соответственно, и их форму мы будем называть «чувственно-непосредственными».

Сопоставление двух сходных отношений, уже фиксированных в абстракции, когда одно отношение становится мерой другого, другое определяется относительно первого, — такое сопоставление и опосредствование исследуемого свойства даёт нам количественное отношение и, соответственно, количественную абстракцию.

Абстракция движение является качественной. Она выражается отдельным словом, и такая форма вполне соответствует содержанию качественной абстракции. Абстракция скорость на этом этапе также выражается отдельным словом, но эта форма сама по себе уже не может выразить содержания количественной абстракции; последнее для своего выражения нуждается в иной, более сложной форме. И это противоречие между наличным содержанием и наличной формой является одной из причин, определяющих дальнейшее развитие понятия.

На втором этапе развития понятия скорости осознается роль третьего тела — земли или места. Ситуация, то есть система отношений, отражавшаяся в понятии (в его содержании отражалась исследуемая сторона объекта, а в его строении в «снятом» виде — опосредствующие отношения), расчленяется, дифференцируется. Вырабатываются абстракции пути и времени. (Мы оставляем в стороне вопрос о том, как образуются эти абстракции.) Различие скоростей двух движений начинают сознательно выражать в сравнительной оценке длин пройдённого за одно и то же время пути или в сравнительной оценке времени, затраченного на то, чтобы пройти один и тот же путь. Так, например, Аристотель пишет, что более скорому из двух тел необходимо «в равное время двигаться больше другого, в меньшее одинаково или в меньшее больше, как и определяют некоторые слово скорее» [Аристотель, 1937 с, VI, с. 126]. И в другом месте: «… Если всякое тело должно двигаться (по одному и тому же пути. — Г. Щ.) или равное время с другим, или меньшее, или большее и двигающееся больше времени является более медленным, равное время равноскоростным, а более скорое не является ни тем, ни другим, то оно будет двигаться ни больше, ни равное время. Остаётся, следовательно, меньшее…» (там же, с. 127).

При этом нужно отметить, что время как таковое не измерялось. В первом случае время прямо фиксировали как равное и сравнивали между собой отрезки пути, а во втором — выделяли определённый отрезок пути и следили, какое из тел достигает его конца раньше, какое позже. В обоих случаях, таким образом, движения сопоставляли не по отношениям пути ко времени, а только по одной компоненте этих отношений, чаще всего по проходимому телом расстоянию, предполагая вторую компоненту — время — одинаковой для обоих движений и фактически оставляя её в стороне.

Необходимость сравнивать между собой различные длины на определённом этапе развития общественной практики и мышления привела к появлению эталона длины. Пройденные телами расстояния стали обозначаться числами.

Способ сопоставления движений по-прежнему оставался чувственно-непосредственным, так как вплоть до Галилея не существовало часов, пригодных для измерения небольших промежутков времени, и последнее всегда приходилось фиксировать как равное для двух движений путём непосредственно-зрительного их сопоставления.

Однако сопоставление и измерение сложного отношения — движения — удалось свести к сравнению и измерению более простого отношения — расстояний, что позволило выразить «отношение движений» в числовых величинах s₁ / s₂ = α (1). При этом числовая величина α показывала: непосредственно — во сколько раз больше путь, пройденный за определённое время одним телом, чем путь, пройденный за то же время другим телом; опосредствованно — во сколько раз больше скорость движения одного тела, чем скорость движения другого.

Третий этап в развитии понятия скорости, связанный с именем Галилея (XVII век), характеризуется введением эталона движения — часов ³.

В простейшем случае они представляют собой два тела, одно из которых (сейчас — стрелка) движется относительно другого, а другое (циферблат) является масштабом этого движения, дающим ему числовую меру в отрезках пути. Процесс сопоставления двух «естественных» движений может быть разбит на два этапа. Первый состоит в сопоставлении каждого из сравниваемых движений с движением стрелки часов.

Результаты этого сопоставления выступают в виде двух чисел или двух рядов чисел, показывающих величину пути, пройдённого исследуемым движением и движением стрелки за одно и то же время. Второй этап состоит в сравнении этих чисел или рядов чисел между собой.

Отношение 1 показывало, во сколько раз больший путь прошло одно тело в сравнении с другим за одно и то же время. Оба сопоставляемых движения были абсолютно равноправны. Второе было мерой первого, но точно так же и первое могло стать мерой второго. По строению, и в частности по строению самой формы, это математическое отношение давало нам новый вид понятия скорости. Его (совершенно условно) можно назвав «случайным», или «нестандартным».

Беря отношения s₁ / t₁ = α₁и s₂ / t₂ = α₂ (2) мы получаем величины, показывающие, сколько единиц своего пути проходят исследуемые тела, пока стрелка часов проходит единицу своего пути, то есть единицу циферблата. Внутри каждого из этих отношений, если брать их изолированно, сопоставляемые движения и, соответственно, меры пройденных за одно и то же время расстояний s₁ и t₁, s₂ и t₂ по-прежнему абсолютно равноправны. И в этом плане каждое из отношений 2 ничем не отличается от отношения 1. Но если брать отношения 2 во взаимосвязи друг с другом, то оказывается, что непосредственно сопоставляемые движения — движение исследуемого тела и движение стрелки часов — играют уже различную роль. Движение стрелки часов в этих двух случаях (а также и других) выступает в качестве постоянной, а благодаря этому и всеобщей меры движения, в качестве его постоянного эталона. Подобное «выталкивание» всеобщего эквивалента, или эталона, собственно, и превращает отношение 1 в выражение скорости s/t = v, как мы это понимаем сейчас, или, другими словами, даёт всеобщий, «стандартный» вид понятия скорости. Полученное таким путём выражение v = s/t (3) характеризует внутреннюю определённость исследуемого движения значительно точнее, чем все предшествующие. Это определение, так же как и другие, имеет относительный характер, но поскольку оно определяется по отношению к постоянному, одинаковому для всех эталонному движению, то в известных границах его относительность можно не учитывать; оно приобретает видимость абсолютной характеристики.

Сопоставляя величины отношений v₁ и v₂ мы как бы возвращаемся к непосредственному сопоставлению исследуемых движений, «исключаем» эталонное движение стрелки часов.

При определённых условиях полученная формула 3 может быть преобразована в формы s = vt и v = const., которые становятся законами движения исследуемого тела относительно движения стрелки часов.

Таким образом, сложное объективное отношение — движение — осознавалось человеком постепенно, с помощью ряда других, опосредствующих отношений. Только опосредствование и усложнение этого опосредствования позволили выразить движение в абстрактно-логической форме количественного понятия скорости, отличной от непосредственного чувственного образа, причём всё большее опосредствование не удаляло понятие от объекта, а, наоборот, приближало его, ибо позволило схватить закон реального отношения, сделало понятие более адекватным самому объекту мысли.

Менялся характер опосредствующих отношений, и соответственно менялось строение, в частности форма, понятия, хотя объект оставался всегда одним и тем же. Отсюда мы можем сделать вывод, что строение понятия, и в частности строение его формы, отражает ступени опосредствования исследуемого объекта и соответственно типы тех отношений сопоставления, посредством которых в этом объекте выделяются те или иные стороны, то или иное содержание понятия.

Та последовательность этапов, которую мы наметили в развитии понятия скорость, сначала чувственно-непосредственная абстракция, фиксируемая отдельным словом, затем случайная мера, меняющаяся от раза к разу, и, наконец, выталкивание эталона, всеобщей и постоянной меры является, на наш взгляд, общей закономерностью в развитии всех количественных понятий.

***

До сих пор мы говорили о строении понятий и в связи с его изменением намечали этапы развития понятий. Но, кроме того, существуют ещё процессы развития понятий ⁴. Эти процессы точно так же имеют своё строение и подчиняются определённым закономерностям.

Исследование строения процессов развития понятий составляет не менее важную задачу, чем исследование строения самих понятий. Рассмотрим на примере понятия скорости одну весьма общую, на наш взгляд, закономерность в развитии понятий, которую мы будем называть «расщеплением» (или дифференциацией) понятия.

Образовавшееся понятие v = s/t имело задачей характеризовать исследуемое движение, причём, естественно, характеризовать на всём его протяжении. Другими словами, оно должно было быть для него величиной постоянной, или однозначной. В настоящее время мы знаем, что однозначно полученная таким путём величина v может характеризовать лишь равномерные движения и что она неприменима для описания переменных движений. Этот факт был осознан не сразу, и осознание его представляет собой определённый процесс развития нашего знания.

Различие между равномерными и переменными движениями стало известно людям уже давно. Но это было лишь наглядное, чувственное значение, не осмысленное в понятиях. Существовавший во времена Аристотеля чувственно-непосредственный способ сопоставления движений, когда время фиксировалось как равное, а сравнивались одни лишь отрезки пройдённого телами пути, не позволял выявить различие между равномерными и переменными движениями в виде понятия. Действительно, такой способ сопоставления выделял в движениях лишь одно их свойство — величину перемещения за определённое время, — оставляя другие свойства в стороне. Он нивелировал все движения, сводя их, по существу, к равномерным. Ведь путь как показатель движения безразличен к характеру самого движения; по нему нельзя заключить, как пройдено расстояние, с равномерной скоростью или нет.

Поэтому, сравнивая движения тел по пройденным ими расстояниям, мы фактически «превращаем» эти движения на рассматриваемом отрезке пути в равномерные, и ничто при этом не наталкивает на мысль о неправомерности этого преобразования. Ограничиваясь однократным сопоставлением исследуемых движений, мы исходим из неосознанной предпосылки, что результаты сопоставления, проведённого в какой-то промежуток времени и на каком-то отрезке пути, могут быть распространены на движение в целом; мы исходим из того, что если тело А на сравниваемом отрезке s имело большую скорость, чем тело В на этом же отрезке, то оно и на следующем отрезке пути будет иметь большую скорость, а это справедливо лишь для равномерных движений. Здесь существующий способ сопоставления движений определял границы выявляемого содержания.

Таким образом, хотя в представлении древних понятие скорости было результатом и средством сопоставления движений вообще, независимо от их характера, по содержанию и по своему строению оно служило адекватным отражением только равномерных движений. Поэтому когда Галилей приступил к исследованию ускоренных движений, используя для этого понятие скорости, выраженное в формуле 3, то это привело его к логическому противоречию (антиномии). Так как часы, находившиеся в его распоряжении, несмотря на все произведённые усовершенствования, были все ещё малопригодны для измерения небольших промежутков времени, Галилей решил замедлить исследуемые движения падения с помощью наклонных плоскостей, а это, в свою очередь, заставило его сопоставить между собой падение тел по вертикали и по наклонным. Согласно определениям Аристотеля, из двух движущихся тел то имеет большую скорость, которое проходит за одно и то же время большее пространство, чем другое, или то же пространство, но в меньшее время. Соответственно считалось, что два движущихся тела обладают одинаковой скоростью, если они проходят равные пространства в равные промежутки времени.

Галилея эти определения уже не удовлетворяли. Выработанный им способ измерения времени позволил представить понятие скорости в виде математического отношения величин пути и времени. С этой новой точки зрения ничего не изменится, если назвать скорости равными и тогда, «когда пройденные пространства находятся в таком же отношении, как и времена, в течение которых они пройдены…» [Галилей, 1948, с. 34]. Поскольку Галилей уже «подвел» понятие скорости под более широкое понятие математического отношения, сделанный им переход был вполне законен. Равенство отношений s₁/t₁ = s₂/t₂, как при s₁ = s₂, так и при s_1 ≠s₂, остаётся справедливым, если t₁ и t₂ меняются в той же пропорции, что и пути.

Итак, имеется два определения равенства скоростей двух движущихся тел.

Первое: скорости двух тел равны, если за равные промежутки времени эти тела проходят равные пространства.

Второе: скорости двух тел равны, если пространства, проходимые одним и другим, пропорциональны временам прохождения.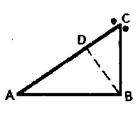

Второе определение является обобщением первого, первое вытекает из второго и должно быть справедливым, если справедливо второе. Имея эти два определения, Галилей приступил к сопоставлению конкретных случаев падения тел. Пусть по СВ и СА (см. схему) падают два одинаковых тела. Скорость тела, падающего по СВ, будет больше скорости тела, падающего по СА, ибо, как показывает опыт, в течение того времени, за которое первое падающее тело пройдёт весь отрезок СВ, второе пройдёт по наклонной СА часть CD, которая будет меньше СВ. Отсюда, в соответствии с первым определением, можно сделать вывод, что скорости тел, падающих по наклонной и по вертикали, не равны.

В то же время известное Галилею положение о том, что скорость падающих тел в какой-либо точке зависит только от высоты их падения, наводит его на мысль, что раз скорости тел в точках А и В, расположенных на одной горизонтали, равны, то они должны быть и вообще равны на отрезках СА и СВ. Он проверяет это предположение на опыте, и действительно оказывается, что отношение времён падения по всей наклонной и по всей вертикали равно отношению длин наклонной и вертикали. Отсюда в соответствии со вторым определением можно сделать вывод, что скорости тел, падающих по наклонной и по вертикали, равны.

Таким образом, следуя рассуждению Галилея, мы получили два противоречащих положения:

«Скорости тел, падающих по СА и СВ, равны».

«Скорости тел, падающих по СА и СВ, не равны».

Причину выявленного Галилеем противоречия нельзя искать в произведённом им обобщении условий равенства скоростей. Если бы мы, пользуясь старым условием равенства скоростей, начали сопоставлять движения шаров по СА и СВ, беря отрезки проходимого пути в разных частях СА и СВ, то мы получили бы и при старом определении весьма противоречивые результаты. Скорость падения шара по СВ могла оказаться в одном месте больше скорости падения шара по СА, в другом — равной, в третьем — меньшей. Таким образом, рассмотренное развитие понятия скорости и обобщение условий равенства скоростей не являлись причиной противоречия, а были лишь случайными обстоятельствами, которые облегчили его обнаружение.

Причина этого противоречия заключена в том, что понятие скорости, сложившееся из сопоставления равномерных движений и однозначно характеризовавшее эти движения, уже не подходит для сопоставления и однозначной характеристики движений неравномерных.

Подобные логические противоречия, или антиномии, можно часто встретить в истории науки. Оба положения такого противоречия в равной мере истинны и неистинны. Истинны в том смысле, что они оба действительны, если мы исходим из существовавшего в то время определённого строения исходного понятия. Неистинны в том смысле, что это строение понятия уже не может дать однозначной характеристики новых исследуемых явлений.

Выявление подобного противоречия наталкивает исследователя на мысль, что он не учёл в понятии какого-то обстоятельства, какого-то свойства исследуемого явления и заставляет искать это обстоятельство или свойство, а затем в соответствии с ним менять всю систему понятий, относящихся к исследуемой области явлений.

Часто противоречие разрешается тем, что рассматриваемое понятие подводится под новое, более общее или более узкое понятие и рассматривается с точки зрения признаков последнего. Так поступает и Галилей.

Сначала он рассматривал скорость как величину или, точнее, как математическое отношение, а после выявления противоречия, стремясь объяснить его и «снять», он начинает рассматривать скорость как переменную величину или переменное математическое отношение. Это было облегчено тем, что представление о переменных величинах к тому времени уже сформировалось (см., например, [Гуковский, 1947, с. 177–180, 469–474; Hall, 1954, с. 80–85]).

Галилей ставит вопрос о законе изменения этой величины в случае свободного падения тел на землю и предполагает, что оно происходит по «простому» закону v = аt, подобному закону изменения пути в равномерном движении, и таким образом находит новую величину (a — ускорение), однозначно характеризующую свободное падение тел. Закон, связывающий движение свободно падающего тела с движением эталона (стрелка часов), принимает вид: s = аt₂ / 2 (4). Величина a характеризует «внутреннюю определённость» или качество каждого отдельного равномерно-ускоренного движения.

Заметим, кстати, что дальнейшее усложнение строения и, соответственно, формы закона, связывающего исследуемое движение с движением эталона, как всегда, обусловлено усложнением степени опосредствования, усложнением опосредствующих отношений между исследуемым движением и движением эталона. Но если раньше опосредствующее сопоставление носило предметно-практический характер, то теперь в формуле 4 последняя ступень опосредствования носит абстрактно-логический, формальный характер. Величина v, полученная из математического отношения пути к времени и поэтому непосредственно недоступная чувствам, сопоставляется с движением эталона чисто умозрительным, спекулятивным путём, посредством применения уже выработанной связи v = at, подобной s = vt. Элементы а и t выступают в качестве абстракций, с помощью которых мы формально анализируем логически-опосредствованно образованную абстракцию v. (Мы ограничимся этим замечанием, так как в нашу задачу не входит исследование специфики чисто формальных процессов мышления.)

Выявление нового свойства в процессах движения заставляет Галилея пересмотреть все относящиеся к ним понятия. Так, например, Галилей даёт следующее определение: «Движением равномерным или единообразным я называю такое, при котором расстояния, проходимые движущимся телом в любые равные промежутки времени, равны между собой.

Пояснение. К существовавшему до сего времени определению (которое называло движение равномерным просто при равных расстояниях, проходимых в равные промежутки времени) мы прибавили слово «любые», обозначая тем какие угодно равные промежутки времени, так как возможно, что в некоторые определённые промежутки времени будут пройдены равные расстояния, в то время как в равные же, но меньшие части этих промежутков пройденные расстояния не будут равны» [Галилей, 1934, с. 282–283].

Исследование неравномерных движений показывает, что скорость на каком-либо отрезке пути этого движения иная, чем на соседнем. Но и на протяжении первого отрезка скорость непостоянна. Этот отрезок содержит в себе несколько меньших отрезков, на каждом из которых скорость имеет свою особую величину. И на протяжении любого из этих меньших отрезков скорость также не остаётся постоянной. Продолжение такого деления — а к нему исследователи должны были обязательно прийти, сознательно или бессознательно, — приводит их к необходимости ввести понятие скорость в точке. Эта необходимость проявилась уже тогда, когда, исследуя ускоренные движения, стремясь свести их к равномерным, стали говорить о конечной скорости какого-либо ускоренного движения, то есть о скорости, достигнутой в последней точке рассматриваемого отрезка пути (см. [Гуковский, 1947, с. 177–180, 469–474; Wilson, 1956, с. 121]). Однако вплоть до возникновения дифференциального исчисления это и подобные ему понятия о мгновенных, или «точечных», характеристиках не могли стать «рабочими», то есть действующими.

Дифференциальное исчисление, развитое Ньютоном и Лейбницем, дало правила получения бесконечно малых характеристик из чувственно воспринимаемых и измеряемых отношений, установило правила оперирования с подобными характеристиками. В результате этого понятие скорости расщепилось на два понятия: средняя скорость и мгновенная скорость. Эти понятия имеют не только различное содержание, но и различное строение. Действительно, они измеряются различным образом и выражаются в различных формулах. Первое предполагает лишь эмпирически измеренные величины времени и пути, пройдённого телом, и определяется как их простое алгебраическое или арифметическое отношение. Закон движения для этого понятия безразличен, или, вернее, оно все движения сводит к движению, подчиняющемуся закону v = const., где v определяется из математического отношения любых соответствующих друг другу s и t. Второе, то есть понятие мгновенной скорости, не может быть найдено и вообще не имеет практического смысла, если мы, кроме эмпирических данных s и t, не имеем ещё закона исследуемого движения, выраженного в формуле или в графике. Величина мгновенной скорости в общем случае выражается в виде функции и определяется с помощью операции дифференцирования, производимой над этой формулой. Только для равномерных движений форма выражения мгновенной скорости совпадает с формой выражения средней скорости, для остальных же движений они не совпадают.

Таким образом, процесс расщепления понятия складывается из двух весьма различных частей: 1) получение пары противоречащих положений типа «А есть В, А не есть В»; 2) образование новых понятий и изменение старых.

Как мы видели, вторая часть этого процесса обособлена и зависит от характера рассматриваемых объектов и степени их познания. Тем не менее, взятый в целом, процесс дифференциации понятий имеет постоянное строение и является одним из наиболее общих процессов развития понятий. Лишь только какое-нибудь свойство, считавшееся до того простым и абсолютно сходным в ряде объектов мысли, начинают рассматривать с новой точки зрения, то есть в других условиях и при других отношениях между предметами и явлениями, как оказывается, что это свойство не абсолютно сходно во всех рассматриваемых объектах, что оно наряду со сходными моментами несёт в себе различия. Оказывается, что абстракция, отражавшая общее сходное свойство этих объектов мысли, недостаточно точна, поверхностна и должна расщепиться на ряд новых абстракций, отражающих эти различия.

С процессом дифференциации понятий мы встречаемся на каждом шагу при изучении истории науки. Можно привести в качестве наиболее ярких примеров знаменитый спор Бертолле и Пру (1801–1808), в результате которого понятие соединения раздвоилось на понятие соединение и смесь, опыты Галилея над соударением тел, в ходе которых он пришёл к необходимости разделить существовавшее тогда понятие силы на два: силу удара и силу давления. Можно указать на продолжительные споры, развернувшиеся с XVII века вокруг понятий силы, живой силы, количества движения и других, которые закончились лишь в XIX веке тем, что от понятия силы окончательно откололось понятие энергии. Понятие массы прошло в своём развитии через целый ряд дифференциаций (масса инертная, масса тяжёлая, масса покоя, масса движения и другие). В истории политической экономии можно указать на противоречие: товары всегда продаются по их стоимости; товары никогда не продаются по их стоимости, — разрешённое К. Марксом путём разделения понятий стоимости и цены производства и выяснения взаимоотношения между ними.

Число этих примеров можно было бы умножать без конца, так как дифференциация понятий происходит на каждом шагу процесса познания. Чаще всего она проходит менее заметно ⁵ и занимает не столь видное место в истории развития науки, как указанные примеры, но это зависит уже от содержания понятий и их значения в системе той или иной науки, а не от логического строения процесса их развития.

Строение процесса дифференциации, понятно, можно было бы проанализировать на любом из этих примеров. Но мы не случайно выбрали именно понятие скорости. Настоящая работа носит не историко-научный, а логический характер, то есть ставит перед собой задачу не разъяснения содержания того или иного сложного и запутанного понятия, а выявления общих характеристик строения нашей мысли. Поэтому мы должны были взять не эти важные и сложные понятия, а любое уже устоявшееся и простое понятие, которое не вызывало бы споров по своему содержанию и позволило бы благодаря этому выявить с наибольшей наглядностью и отчётливостью общие закономерности процессов развития строения научных понятий. С этой точки зрения механическое понятие скорости было самым подходящим.

***

На основе исследования процесса расщепления понятий мы можем построить новую схему умозаключения. Из посылок «А есть В», «А не есть В», относящихся к одному и тому же явлению, при условии, что оба эти положения получены путём «правильных» умозаключений, мы можем сделать вывод, что реальное содержание рассматриваемого явления не соответствует строению, в частности мысленному содержанию и строению формы, прилагаемого к нему понятия. Мы должны искать в рассматриваемом явлении свойство, которое не отражено в понятии и которое в то же время играет существенную роль при заданном анализе этого явления.