|
Спиридонов Владимир Феликсович — доктор психологических наук, доцент Института психологии имени Л. С. Выготского Государственного педагогического университета имени А. И. Герцена (РГГУ). Основные направления научной деятельности: психология решения задач и проблем эвристики, классификация мыслительных задач, феномен высокого профессионализма. |
|
ВведениеВклад психологии в разработку гуманитарных и иных технологий противоречив, а местами даже сомнителен: успехов здесь меньше, чем разочарований и несбывшихся надежд. Особенность этой ситуации, к тому же, заключается в поразительном несовпадении существующих в обществе ожиданий и реальных свойств и возможностей психологических методов. Психологи в различных сферах своей исследовательской или практической деятельности регулярно сталкиваются с запросом на прямые способы воздействия на человека для достижения В качестве наглядного примера такого состояния дел процитирую весьма показательное исследование, проведённое несколько лет назад на материале психотерапии (Райнаи Г., Столин В. В., 1989). Психотерапевты и люди, не имеющие опыта общения со специалистами такого типа, были опрошены определённым образом на предмет их представлений о психотерапевтическом процессе. Результаты обнаружили существенные различия, доходящие до полной противоположности. Так, «люди с улицы», помимо прочего, надеялись на получение конкретных советов, касающихся готовых способов разрешения проблемных ситуаций, в которые они попали. Они выказывали готовность прислушиваться к рекомендациям и скрупулёзно их реализовывать. Понятно, что ответственность за выработку «рецептов» и за ожидаемый результат оказывалась в этом случае целиком снятой с плеч клиента, который выступает лишь исполнителем чужого решения. Авторы называют такую модель ожиданий «медицинской» по аналогии с обычным визитом к врачу, который прописывает вам необходимые снадобья, апеллируя только к вашей готовности пить таблетки, но не участвовать в выработке способов лечения. Психотерапевты, напротив, рассчитывали на совместную с клиентом работу, направленную на прояснение сложившейся проблемной ситуации и на поиск путей решения. В этом случае ответственность за искомый результат оказывалась разделённой между обоими участниками процесса. Сама возможность априорных готовых указаний клиенту вызывала у психотерапевтов резкое отторжение. Из их ответов становилось понятно: простых «отмычек» к человеку и его сложным проблемам не существует. Очевидно, что приёмы прямого воздействия 1 (вызывающие энтузиазм у широкой публики и явный скепсис у профессионалов) значительно более похожи на традиционно понимаемые технологии, приводящие к устойчиво воспроизводимому полезному результату, чем предлагаемые психологами не слишком формализованные и не гарантирующие повторяемости процедуры. Однако эти свойства — неизбежная плата за попытки вступить в диалог с «живым» человеческим сознанием, и они в равной мере характерны для большинства гуманитарных «технологий». В центре моего анализа будет находиться один из самых сложных и трудно технологизируемых психологических процессов — решение задач и проблем. Исследование мышления, в частности, продуктивного (творческого) мышления представляет собой один из самых противоречивых разделов психологии. В соответствии с устойчивой традицией психологов интересует не «чистый», а вполне реальный процесс решения, осуществляемый человеком или группой решателей 2 и укоренённый в их жизнедеятельности, то есть связанный с наличной мотивацией, целями, эмоциями, уровнем развития способностей, структурой имеющихся знаний и так далее. Его основная форма — решение проблемных ситуаций: задач и слабоструктурированных проблем. Люди сталкиваются с ними в самых разных сферах практики — проектирование, изобретательство, менеджмент, исследование, обучение специалистов различного профиля и так далее. Это влечёт за собой очевидную потребность в знаниях о строении мышления (как «успешного», так и делающего ошибки) и в надёжных и эффективных методах решения (их обычно называют эвристики или эвристические стратегии) 3, пригодных для широких классов проблемных ситуаций. Такой подход позволяет обсудить и некоторые «рецепты» развития профессионального мышления — мышления специалиста в той или иной предметной области. Что такое задача?С чем сталкивается мышление? Что ему противостоит, создавая «барьеры» и «препятствия» на пути мыслительного процесса? Что вообще может сопротивляться мышлению? Эти вопросы при всей их сложности допускают прямые (хотя и дискуссионные) ответы: только само мышление и может выступать для себя подобным препятствием, хотя это обстоятельство всегда замаскировано каким-то конкретным материалом или ситуацией, с которыми не удаётся совладать. Из сказанного становится понятен феномен мыслительной задачи. Это определённого рода ловушка (специально изготовленная или возникающая стихийно), попадая в которую человеческое мышление сталкивается с собственной неполнотой, неточностью или неадекватностью. Скажем, одно суждение противоречит другому, или одни мыслительные структуры не соответствуют другим (например, представление задачи — разрешённым интеллектуальным операциям), или иррелевантные условия задачи маскируют основные. Не претендуя на построение универсального обобщения, попробую сформулировать понятие текстовой задачи, на примере которой будут рассмотрены структура и закономерности процесса решения. Начну с того, что к такой задаче нельзя относиться как к повествовательному тексту, просто описывающему какую-то реальную ситуацию. Подобная задача целиком условна: все яблоки в ней одинаковы и взаимозаменяемы, поезда движутся строго равномерно и прямолинейно, рабочие никогда не выпускают брак, вода в трубах не кончается и так далее. Причём Подобной же условностью характеризуются и получаемые решения, которые оказываются принятыми или отвергнутыми как «правильные» или «неправильные» на основании конвенций, возникающих ad hoc по ходу решения или сформулированных заранее. Например, является ли знаменитый поступок Александра Македонского, который разрубил «гордиев узел» 5, вместо того чтобы развязать его, решением данной задачи? По условиям, конечно же, требовалось именно развязать узел, но, тем не менее, «ответ» Александра был принят и современниками, и потомками и даже стал нарицательным. Это значит, что задача содержала нечто, что допускало подобную интерпретацию, и это нечто и было выявлено легендарным решением. В соответствии с известным определением (Леонтьев А. Н., 1965; Петухов В. В., 1987), мыслительная задача — цель, поставленная в определённых условиях, препятствующих её непосредственному достижению. Процесс решения здесь — достижение уже заданной, психологически очерченной цели. Он заключается в поиске необходимых для этого средств (которые изначально отсутствуют) в границах, намеченных условиями. Однако более глубокие свойства задачи при таком взгляде остаются за скобками. Под поверхностью оказывается необходимые, но исходно скрытые возможности 6, которые потенциально могут стать основой для решения. Этим задаются объективные поле и границы поиска ответа. Конечно, задача — интенциональное образование, побуждающее решателя к активности, направленной на выявление этих возможностей, что обеспечивается наличием цели. Однако не произвольных, а именно тех, которые могут быть обнаружены в наличных условиях. При отсутствии таковых мыслительная задача превращается в пародию на саму себя 7 и, строго говоря, не является задачей. Но самым сильным свойством текстовой задачи выступает следующее: возможности создают основу для построения системы новых («вторичных») значений, отсутствующих в условии. В ней данное и искомое 8 оказываются взаимоувязанными и определёнными одно через другое. Понятно, что подобная система, возникающая по ходу решения, задаёт и границы условности, и параметры оценки правильности ответа, и допустимые интерпретации задачи. Процесс решения задачи: карта и территорияПроцесс решения мыслительной задачи организован как построение вторичной моделирующей системы 9. Она не присутствует в готовом виде до его начала и может не возникнуть в его ходе — тогда решение останется ненайденным. Решатель образовывает вторичные значения ключевых аспектов задачи — они постепенно оказываются увязанными в единую структуру и определёнными друг через друга. Так реализуются возможности, заложенные в тексте задачи. Это обеспечивает решателя ориентирами для дальнейшего движения: возникающая система все строже и последовательнее определяет и «подсказывает» допустимые способы действия, помогая различать осмысленные и ошибочные шаги. Собственно, в построении такой системы и заключается основной шаг к решению — оно также оказывается заданным и определённым в рамках этого складывающегося целого. Понятно, что вся эта конструкция получается до некоторой степени условной — опирающейся на определённые допущения (например, возьмём за х расстояние между городами А и Б). Однако её жесткости (особенно на ранних стадиях процесса решения), конечно же, недостаточно, чтобы вообще избежать ошибок. Для более наглядного описания вторичной моделирующей системы воспользуюсь метафорой «карты и территории». Она была предложена А. Кожибским и широко использована Г. Бейтсоном (2000) для описания разноплановой реальности (в первую очередь, процессов межличностной коммуникации). Территория, в соответствии с данной метафорой, сложена из объектов, которые обладают собственной «плотностью», «законами взаимодействия» и за счёт этого «оказывают сопротивление». Их нельзя игнорировать или изменить по собственному произволу, поэтому приходится учитывать их свойства в своих действиях. Карта является знаковой системой, которая описывает и представляет территорию, выступающую референтом, то есть набором явлений и связей между ними, обозначаемых данной знаковой конструкцией. Таким образом, отношение карты к территории является референцией 10. Хотя карта и территория тесно связаны между собой, они — принципиально разнородные явления. Карту надо уметь создавать: существуют определённые правила «картирования» — она не может быть целиком произвольной. Карта условна, изменения на ней не влияют на территорию, она может быть неверной в целом или содержать локальные ошибки, ей надо уметь пользоваться, поскольку она включает условные обозначения. Одной и той же территории могут адекватно соответствовать разные карты, причём их количество может быть достаточно велико. При этом на разных картах одной и той же задачи значимые элементы вполне могут не совпадать между собой. Карты могут отличаться друг от друга степенью своей детализированности («масштабом»). Более мелкие объекты встроены в более крупные и исчезают или появляются на карте при изменении масштаба рассмотрения. Принципиально важно не путать карту и территорию (то есть сами объекты и их описание) в ходе решения, поскольку такое смешение ведёт к серьёзным ошибкам. Все сущности, на которые указывает метафора, — реальные составные части процесса решения. Решатель на сновании условий задачи (её текста) производит различение карты и территории, то есть обнаруживает и фиксирует значимые элементы проблемной ситуации: какие предметы или процессы и их количественные показатели присутствуют в условии, как они связаны между собой, что дано и что нужно узнать и тому подобное. Назовём этот процесс референцией–1, а его результат — картой–1. Все названное совершается средствами естественного языка: решатель фиксирует словами открывающееся ему состояние дел. Текст задачи сам по себе не является территорией (то есть фиксированным набором объектов и их свойств), а только даёт Карты–1 недостаточно для решения, поскольку ответ текстовой задачи может быть сформулирован лишь на «языке» вторичных значений. Чтобы справиться с большинством известных проблемных ситуаций, решатель вынужден провести ещё одно картирование: отталкиваясь от карты–1, произвести референцию–2 и построить карту–2 (см. рисунок 1). Референция–1 и —2 кардинальным образом отличаются друг от друга. Референция–2 — значительно более строгий и определённый процесс. Наиболее заметным он становится, когда используется какая-либо знаковая система, отличная от естественного языка. Решатель извлекает из карты–1 определённое содержание (значимое, если он движется в правильную сторону) и фиксирует его средствами этой знаковой системы, то есть с помощью Рисунок 1. Организация процесса решения текстовой задачи: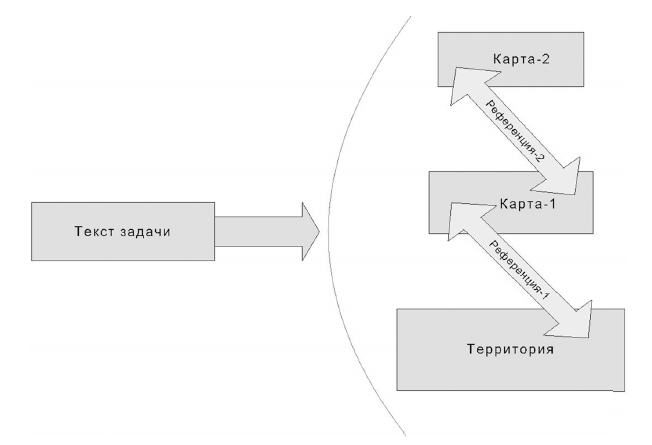
В основе построения карты–2 лежит важная психологическая структура — интеллектуальный инвариант или переменная высокого порядка, которая обеспечивает референцию–2 (Спиридонов В. Ф., 2003; 2004). Мотивировка этого термина заключается в том, что за счёт инварианта задача сохраняет своё единство, несмотря на самые разные допустимые трансформации (например, построение несводимых друг к другу корректных уравнений или их систем). Значение этой структуры чрезвычайно велико: она играет роль связки между картой и территорией. В случае традиционной географической карты в этом качестве выступают картографическая проекция, которая устанавливает зависимость между географическими координатами точек земного эллипсоида и прямоугольными координатами тех же точек на плоскости, и система определённых условных обозначений. В ходе решения задачи такую нагрузку несёт интеллектуальный инвариант. Поэтому его использование позволяет решателю построить адекватную карту–2. Конечно, можно ошибиться и решая правильно составленное уравнение, но это будет техническая ошибка, а не ошибка референции. Интеллектуальный инвариант выступает в качестве своеобразной «модели для сборки» 13. Именно его должен выделить с опорой на условия проблемной ситуации (это случай учебной задачи) или применить к данному материалу (в случае задачи реальной) решатель. В итоге он организует данное и искомое за счёт формулирования новых значений элементов задачи. Таким образом, можно говорить об организующей функции интеллектуального инварианта. В ходе решения переменная высокого порядка выполняет ещё несколько функций. Поскольку интеллектуальный инвариант обладает существенной структурной жёсткостью, то он обеспечивает связность процесса решения, несмотря на то, что обычно задачу можно решить несколькими разными способами (часто весьма далёкими друг от друга). Причём их единство обеспечивается не содержанием задачи, а исключительно отношениями между картами и территорией (подробнее см. ниже). Так выявляется связующая функция. Кроме того, интеллектуальный инвариант выступает объективным основанием для объединения мыслительных задач в родственные группы или «семейства». Задачи, которые в силу своего содержания и структурных особенностей предоставляют решателю сходные возможности, являются зоной использования одного и того же инварианта (особенно наглядно это видно на специально составленных учебных задачах). Так удаётся очертить классифицирующую функцию. Ещё раз обращу внимание на ограниченный (обедненный и условный) характер территории, к которой апеллирует задача. Именно поэтому инвариант и может связать её с той или иной картой. При этом в качестве самих интеллектуальных инвариантов могут выступать чрезвычайно разноплановые явления: понятия, противоречия, схемы, абстрактные образы, метафоры и так далее. Все они несут возможность организации сложного материала, поэтому их роль при создании карты–2 в ходе решения самых разных задач представляется одинаковой: применение инварианта (или обнаружение его в учебной задаче, куда он предусмотрительно «заложен» её авторами) — устойчивый «культурный» способ решения мыслительных задач. Эффективность вторичной моделирующей системы в рамках процесса решения нетрудно объяснить. Именно совместное использование двух знаковых систем позволяет выделить и увязать в рамках единой конструкции данное и искомое задачи, то есть организовать материал проблемной ситуации таким образом, чтобы построить значения ещё не известных её частей. Кроме того, в этой ситуации выступают на первый план новые денотаты, то есть объекты и их соотношения, которых в явном виде не было в условии. Замечу, что возникающая система вторичных значений никак не нарушает феномена творческой задачи, поскольку не несёт готового ответа и даже способа его получения, а лишь предоставляет способы для его выражения и функциональные требования, которым он должен соответствовать. Также легко видеть, что описанная теоретическая конструкция не претендует на универсальность: существуют виды задач, решение которых не требует построения вторичной системы значений. Возникающая в структуре решения вторичная моделирующая система играет ещё одну важную роль — она задаёт границу корректности и осмысленности самих текстовых задач. Для проблемных ситуаций типа «В магазин привезли 100 кг яблок по 30 рублей за килограмм и 150 кг груш по 40 рублей за килограмм. Всего привезли 300 кг фруктов. Сколько стоят все привезённые фрукты?» или «Слон весит больше одной тонны, а кит больше двух. Кто кого переборет?» достаточно легко показать невозможность построения карт — противоречивость или недоопределённость территории буквально бросается в глаза. Но с задачами типа «Рабочий кружок, состоящий из двадцати взрослых и подростков, устроил сбор денег на покупку книг, причём каждый взрослый внёс по 3 рубля, а каждый подросток — по 1 рублю. Сколько было в этом кружке взрослых и подростков, если всего было собрано 35 рублей?» или «Отцу 32 года, сыну 5 лет. Через сколько лет отец будет в 10 раз старше сына?» дело обстоит сложнее (примеры из Фридман Л. М., 2001; Перельман Я. И., 1978). Корректно составленное уравнение для первой из них [3 (20 - Х) + Х = 35] приводит к ответу Х = 12,5 подростка, а для второй [32 + Х = 10 (5 + Х)] — к ответу Х = — 2 года. Дробное количество людей в первом случае не удаётся интерпретировать относительно какой бы то ни было связки карты и территории: задача оказывается некорректной. Однако во втором случае референция возможна: ответ означает, что требование выполнялось два года назад. Задача сохраняет осмысленность и остаётся корректной 14. Наконец, описанные свойства вторичной моделирующей системы могут быть использованы в качестве надёжного критерия выделения мыслительных процессов, дополняющего традиционные определения, идущие ещё от вюрцбургских психологов. Если в ходе решения мыслительной задачи происходит создание системы связанных между собой вторичных значений элементов проблемной ситуации, мы можем констатировать (да и документировать): мышление имело место. ПарадигмаВ гуманитарных науках (прежде всего в языкознании) созданы удобные способы фиксации системного строения изучаемых объектов. Одним из них — построением парадигмы — я и воспользуюсь для описания полной структуры решения мыслительной задачи. Понятие парадигмы (греч. пример, образец) было введено в античной грамматике для упорядочивания возможных форм варьирования одного слова. Ныне так называют любой класс лингвистических единиц, с одной стороны, противопоставленных друг другу, но при этом соположенных по какому-то признаку. Парадигматические отношения — отношения единиц в системе языка — противополагаются синтагматическим, возникающим в речи или тексте. Парадигма позволяет не только структурировать анализируемый материал, но и выявить принципы самой этой организации. Особенное значение подобного метода анализа в нашем случае состоит в том, что он позволяет выявить и систематизировать все корректные возможности, которые содержатся в условии задачи, а не только некоторые, реализованные в экспериментальных протоколах. Кроме того, построение подобного описания является лишним аргументом в пользу реальности вторичной моделирующей системы в мыслительном процессе. В качестве материала для описания используем широко известный класс проблемных ситуаций — текстовые задачи по алгебре. Они представляют собой пример так называемых неинсайтных или понятийных задач (в работе Спиридонова В. Ф., 2006-а, предлагалось именовать их регулярными). Такие задачи несут в своей структуре регулярности определённого рода, что в значительной мере определяет особенности процесса их решения. К этому типу также может быть отнесено большинство проблемных ситуаций из школьных учебников математики, физики, химии и так далее. Подобные задачи открывают возможность выделения данного и искомого и их координации между собой посредством обобщённого принципа (понятия, правила, определения, таксономии, уравнения и тому подобное). Понятие функции /y = f (x)/ 15 играет ключевую роль в построении карты–2 в ходе решения текстовых задач по алгебре по крайней мере, в пределах школьной программы). При этом данная психологическая структура выступает не в качестве формы обобщения, а как способ организации и представления содержания проблемной ситуации. В условии обсуждаемых задач можно обнаружить связанную пару величин (иногда больше), которая не определена количественно и не может быть непосредственно вычислена. Так, в задаче «На автостоянке находятся машины — автомобили и мотороллеры. У них вместе 100 колес и 40 рулей. Сколько тех и других машин?» такой парой является соотношение между количеством мотороллеров (х) и количеством автомобилей (40 - х). Собственно, это и есть «минимальная» функция (здесь: y = 40 - х). Мы будем называть её «функциональной связкой». Её удобно использовать для построения новых значений элементов проблемной ситуации. Из подобных и более сложных частей и конструируется уравнение, с помощью которого решается задача. Безусловно, и полное уравнение является функцией, но зафиксированной в более крупном масштабе: меньшие конструкции «вложены» в неё. Принципиально важно, что в обсуждаемом случае значения всех элементов будут увязаны друг с другом и реализованы на одном «языке» — выражены через одну и ту же неизвестную величину (х). Не менее важно, чтобы между парой величин, составляющих функциональную связку, было задано как минимум два отношения (в приведённом примере это сумма колес и сумма рулей). Если такое правило выполняется, то задача объективно относится к обсуждаемому классу и решается уравнением. Если отношение всего одно — к структурно более простым проблемным ситуациям. Проиллюстрирую процесс складывания системы вторичных значений выдержками из экспериментального протокола: Исп. А. Н., 19 лет. И: «Имеются кролики и клетки. Если в каждую клетку посадить по одному кролику, то один кролик останется без места. Если в каждую клетку посадить по два кролика, то одна клетка окажется пустой. Сколько кроликов и клеток? Э: О чём ты думаешь? И: Я пытаюсь решить задачу. О чём я думаю… Ладно, я попробую сначала, наверное, привычным способом, что ли. А потом, может… Предположим у нас есть x клеток. Тогда если записать первое условие, то кроликов у нас будет x + 1. Это кролики. Ну да, в каждой клетке по одному кролику, один кролик без места. Кроликов на одного больше. Здесь у нас другая пропорция: если у нас есть x клеток, в каждой клетке по 2 кролика, то тогда у нас количество кроликов будет (x — 1) 2 это кролики. И судя по всему, тогда x + 1 = 2 (x — 1)» и так далее (отточиями обозначены паузы в рассуждениях испытуемого). Возникновение новых значений элементов решаемых задач здесь представляется очевидным. В соответствии с изложенными теоретическими представлениями, инвариант-функция оказывается единым для разных по содержанию (движение, работа, состав числа и тому подобное) и математической форме текстовых алгебраических задач (то есть решаемых с помощью квадратных или линейных уравнений). В простых случаях (скажем, задача из школьной программы) переменная высокого порядка в латентной форме «существует» до начала решения — авторы учебника позаботились о необходимом и достаточном характере условий, способствующем её применению. В случае реального творчества в области математики, логики, естественных наук и так далее создание инварианта (скажем, выстраивание системы обобщений) или применение его к новому материалу (например, проверка новой функциональной зависимости) выступает необходимым моментом решения, но такая возможность ничем не гарантирована. В таблице № 1 приведены тексты стандартных алгебраических задач 16, наглядные схемы их описания 17 и набор уравнений, составляющих парадигму для каждой из них. Кроме того, выделены функциональные или количественные соотношения, варьирование которых и позволяет составить парадигмальные уравнения. Поскольку алгебраически все возможные уравнения равноправны, в качестве дополнительного критерия отбора было использовано отношение карты и территории: обе части уравнений, включённых в парадигму, должны иметь «предметную» интерпретацию, то есть должны быть количественно истолкованы в терминах условий задачи 18. Кроме того, в качестве примеров я ограничился лишь единичными уравнениями; способ анализа и упорядочивания систем уравнений ничем не отличается от приведённого и лишь увеличивает объём описания каждой конкретной задачи. Замечу также, что в качестве примера приведены «корректные» парадигмы, в которые включены лишь правильные уравнения. Понятно, что на следующем шаге они могут быть использованы как средство упорядочивания и анализа коллекции ошибочных решений. Обращает на себя внимание несколько структурных особенностей построения обсуждаемого класса задач. Даже на локальных примерах, приведённых в таблице, можно обнаружить постепенное сокращение информации, которая содержится в условии. Вместо количественно заданных величин (скажем, скорость поезда равна 57 км/ч) в условии все в большем количестве начинают присутствовать функциональные связки. В самых неопределённых случаях задача целиком состоит из них (см. таблицу № 3). Таблица № 1. Парадигмы стандартных алгебраических задач: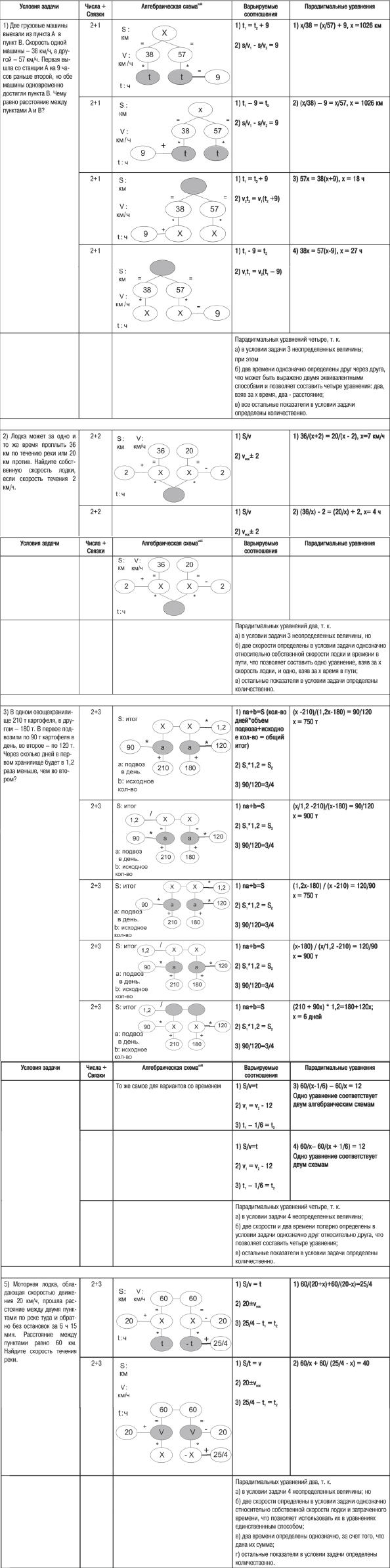
Таблица № 2. Примеры пограничных с арифметическими задач: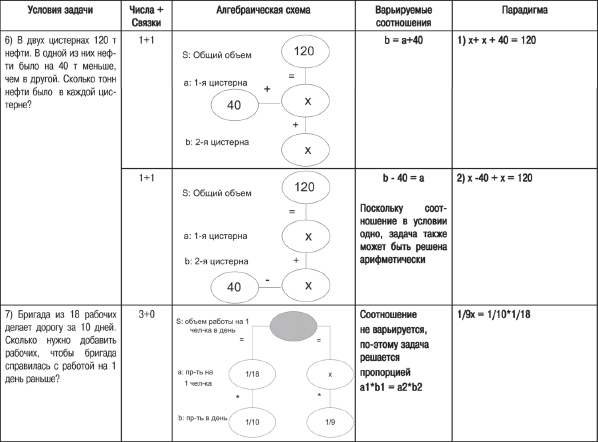
Соотношение численных данных и функциональных связок определяет структурную сложность задачи (и, следовательно, степень её трудности для решения). Параллельно с нарастанием такой сложности можно видеть увеличение количества парадигмальных уравнений. Интересно, что их количество связано со структурными факторами и не зависит от того, решается ли задача линейным или квадратным уравнением. Замечательным свойством парадигмы оказывается четность, то есть четное количество составляющих её уравнений. Это происходит в силу того, что варьируемые функциональные признаки обычно имеют два значения (например, скорость одного поезда на 10 км больше скорости другого: х 1 + 10 или х 2-10), каждое из которых позволяет составить уравнение. С этим же обстоятельством связана «внутрипарная» сводимость подобных парадигмальных уравнений. При этом сами пары обычно оказываются несводимыми между собой. Используемый метод анализа позволяет однозначно отличить стандартные алгебраические задачи от более простой их разновидности, пограничной с задачами арифметическими (см. таблицу № 2). Легко видеть, что именно выделенные в нашем анализе структурные признаки и оказываются здесь различительными. В первом из приведённых примеров между парой величин в условии (объёмами цистерн с нефтью) задано всего одно отношение, поэтому задача может быть решена с помощью арифметических действий. Во втором условия содержат три количественные величины, что также допускает арифметический путь к решению. В таблице № 3 приведены примеры ещё одной разновидности алгебраических задач — так называемых «вырожденных». Таблица № 3. Парадигмы «вырожденных» алгебраических задач: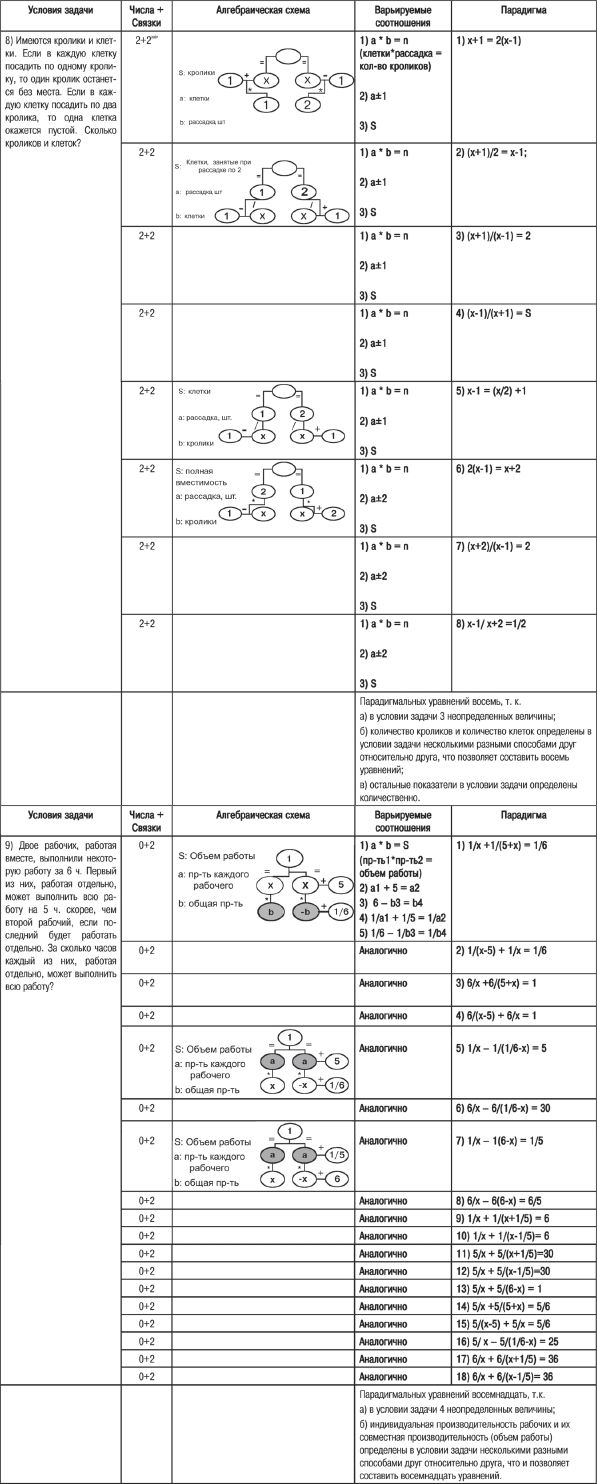
Они являются наименее определёнными — состоящими из одних функциональных связок — и, как следствие, более трудными для решения, чем их информационно насыщенные аналоги из таблицы № 1 (все данные о сравнительной сложности задач заимствованы из работы Спиридонова В. Ф., 2006-б). Количество скрытых возможностей здесь наибольшее, что приводит к резкому увеличению количества уравнений в парадигме. Компетентность в решении задач и развитие профессионального мышленияТезис о существенных отличиях, которые характеризуют успешных профессионалов по сравнению с новичками или менее успешными специалистами в этой же сфере, давно стал общим местом в психологической литературе. Раз за разом психологи выявляют высоко специализированный характер подобных отличий, которые тесным образом связаны с особенностями профессиональной деятельности. Однако первые попытки эмпирически обнаружить какие-либо психологические различия между профессионалами высокого класса (гроссмейстерами — участниками Международного шахматного турнира в Москве в 1925, в котором играли чемпион мира Х.-Р. Капабланка и его ближайшие конкуренты) и «людьми с улицы» оказались обескураживающими. Никаких преимуществ у шахматистов обнаружено не было (Дьяков И., Петровский Н., Рудин П., 1926). Как стало понятно позже, в этом исследовании измерялась степень развития неспециализированных для игры в шахматы познавательных способностей — объём вербальной памяти, скорость простой моторной реакции и так далее. Когда почти через 50 лет психологи смогли пересмотреть область поиска, результаты не заставили себя долго ждать. Оказалось, что релевантные профессиональной деятельности характеристики познавательной сферы шахматистов обладают очень сильно выраженными особенностями. Это касается, например, организации имеющихся у них специальных знаний. Убедительные экспериментальные демонстрации этого обстоятельства принадлежат Г. Саймону, предложившему чёткие процедуры сравнения экспертов (мастеров своего дела) и новичков в различных сферах деятельности. Шахматистам разной квалификации — новичкам и экспертам по российским меркам это были примерно кандидаты в мастера спорта) — предъявляли два типа шахматных позиций для запоминания (Chase W., Simon H., 1973). Сначала были представлены случайные расстановки фигур на доске, а затем реальные позиции, взятые из практических партий. Испытуемые должны были после непродолжительного рассматривания позиции на экране по памяти расставить фигуры, всякий раз начиная с пустой доски. При необходимости позиция предъявлялась несколько раз (но не более семи). Запоминание случайной расстановки выявило некоторое преимущество новичков. Однако при воссоздании второго типа позиций ситуация изменилась на диаметрально противоположную: эксперты за меньшее число предъявлений правильно воспроизводили значительно большее количество фигур на доске, причём часто они ещё успевали верно указать, как лучше играть за белых или за чёрных в данной позиции. Помимо числа предъявлений и ошибок исследователи фиксировали ещё и порядок, в котором расставлялись фигуры. И здесь их поджидал самый интересный результат. Выяснилось, что все испытуемые объединяют фигуры в осмысленные совокупности: они получили название чанков от англ. chunk — порция). Будучи собранными в такие конфигурации, фигуры и расставлялись на доске 19. Именно тут и выступило ключевое отличие между экспертами и новичками: вторые использовали значительно меньшее количество чанков. Более того, для некоторых позиций чанков у них вообще не было, и они переходили на пофигурное воспроизведение (то есть выставляли фигуры по одной). Построение эксперимента позволило оценить количество чанков (в буквальном смысле пересчитать их) у начинающих шахматистов. Число таких конфигураций у новичков не превышало нескольких сотен. Оценить «багаж» экспертов удалось только путём математической аппроксимации: оказалось, что он исчисляется многими десятками тысяч чанков. Таким образом, в явном виде была обнаружена «единица организации» профессионального опыта шахматистов. Более поздние исследования, подтвердив описанные результаты, обнаружили значительное количество других отличительных черт, которыми обладает мышление экспертов 20. К ним можно отнести: наличие чётких схем предметных областей, связанных с проблемой или задачей, и классификацию проблемных ситуаций на основе этих сущностных и весьма обобщённых конструкций; знание слитых со схемой стратегий решения; владение специальными приёмами преодоления сложных проблемных ситуаций. Экспериментально было показано, что эксперты более чётко выделяют и описывают методы решения различных профессиональных проблем (Chi M., Glaser R., Rees E., 1982), намного точнее предсказывают трудности, которые возникнут в ходе решения (Lesgold A., Lajoie S., 1991), более качественно отслеживают применение своих приёмов по ходу решения (Schoenfeld A. H., 1981) и многое другое. Изучение различий между экспертами и новичками при решении текстовых задач потребовало введения новых понятий, отражающих особенности мыслительного процесса. Одним их них было понятие схемы, которая управляет тем, как задача репрезентируется и становится доступной для понимания и оперирования (Chi M. T. H., Bassok M., Lewis M., Reimann P., Glaser R., 1989; Сhi M. T. H., Feltovich P., Glaser R., 1981), или понятие модели, как специального пространства, в котором строятся пробные решения (Holyoak K. J., Thagard P., 1989). В этом контексте изучались дополнительные по отношению к основному решению действия, например, спонтанное использование схем и диаграмм, указывающие, скорее, на поиск пространства для решения, чем направленных на его отыскание (Larkin J. H. et al., 1980). Выяснилось, что эксперты тратят больше времени на подготовку к решению и на освоение особенностей наличной проблемной ситуации, чем непосредственно на поиски ответа. В рамках такой подготовки можно выделить действия так называемого метакогнитивного уровня (Brown A. L., 1980; Flavell J. H., 1985) — в первую очередь, оценку эффективности и оптимальности собственных шагов. Например, было показано, что эксперты имеют большую чувствительность к обнаружению в своём решении ошибок, чем новички (Ohlsson S., 1996; Ohlsson S., Rees E., 1991), и выстраивают по ходу решения специальные процедуры, направленные на исправление сделанных ошибок (Котов Ал. А., 2003). Таким образом, профессиональное мышление представляет собой весьма сложное и многоплановое образование, которое способствует успешному решению его носителем задач и проблем в той или иной конкретной сфере деятельности. Поразительным образом все это многообразное знание о специфике мышления профессионалов высокого уровня практически полностью игнорируется в повседневной практике высшей школы и системе переподготовки кадров высшей квалификации. Коммуникация между психологией решения задач и проблем и этими уважаемыми культурными и социальными институтами в значительной степени нарушена. Скажем, в соответствующей методической литературе доминируют плохо обоснованные нормативные подходы к процессу решения, в соответствии с которыми нужно выделить и транслировать в ходе обучения некоторые интеллектуальные, личностные, поведенческие и тому подобные шаблоны. В соответствии с более ригористической точкой зрения их необходимо целенаправленно формировать у обучаемых 21. Почему в результате таких манипуляций должно возникнуть именно мышление, способное к самостоятельному преодолению профессиональных затруднений, представляет для меня загадку. Памятуя о том, как легко упрощённые психологические идеи становятся рецептами для обучения (стандартная школьная или ВУЗовская подача знаний — из их числа), Предложенная теоретическая модель направлена не только на адекватное описание процессов решения, но и на более глубокое понимание весьма непростого культурного феномена — мыслительной задачи. Проанализированные здесь текстовые задачи по алгебре составляют давно известную, но весьма непростую предметную область, требующую для своей концептуализации достаточно разнообразных теоретических средств. Существуя на границе «чистой» и «прикладной» математики, на стыке понятия и его референта, на взаимодействии формальных и психологических структур, она конденсирует в себе разноплановые возможности для развития индивидуального мышления. Представляется, что традиционное использование этого вида задач в обучении математике, не учитывающее их реальную природу и строение (а соответственно, сложность и состав процессов решения), абсолютно индифферентно к такому развитию. К сожалению, обучение и развитие в таком случае совершаются От внимания обучающих ускользает системный характер строения задач и связанных с ними процессов решения. Это обстоятельство и призван был продемонстрировать проведённый парадигматический анализ. Затруднения, с которыми сталкивается мышление в ходе решения, носят неслучайный характер. Но если подробному описанию предмета обучения (математического, юридического, химического, психологического и тому подобных) посвящены многочисленные усилия, то строение не содержание!) задач, с которыми столкнутся новички в обучении и в своей профессиональной деятельности, связь проблемных ситуаций между собой и с методами решения, за редчайшими случаями, практически игнорируется. Особенно характерно отсутствие метапредметных способов описания задач, независимых от их содержания. Редкие контрпримеры, разработанные для средней школы (см. Балл Г. А., 1990; Фридман Л. М., 2001), лишь подтверждают общую безрадостную картину. Этот пробел и призваны закрыть данные материалы. Однако, чтобы реализовать на материале профессионального мышления известную максиму Л. С. Выготского о том, что обучение ведёт за собой развитие, парадигматического анализа задач недостаточно. Не менее важным выступает трансляция способов «картирования» решаемых проблемных ситуаций во введённом выше смысле). Залог успешного решения профессиональных задач — в научении способам референции (включая выбор удобной для конкретного случая знаковой системы), в прояснении логики построения и использования «карт» и привитии навыков грамотной интеллектуальной работы с опорой на складывающиеся в ходе решения вторичные моделирующие системы. В этом, собственно, и заключается возможный вклад психологии решения задач и проблем в технологии развития профессионального мышления. ЗаключениеДанная работа является комплексом научно-методических материалов для следующих обязательных учебных курсов, преподаваемых на факультетах психологии университетов: «Общая психология», «Общий психологический практикум», «Экспериментальная психология», «Введение в профессию», а также ряда спецкурсов, таких как «Психология решения задач и проблем», «Культурно-исторический подход в психологии», «Методы активизации творческого мышления». |
|
Примечания: |
|
|---|---|
|
|
Библиография: |
|
|
|
Оглавление |
|
|
|