2.1. В каком смысле можно говорить о познании и науке в доантичный периодРяд историков науки уверены, что наука возникла задолго до Античности. А. А. Вайман, один из крупнейших российских исследователей шумеро-вавилонской математики (его книга так и называется «Шумеро-вавилонская математика III–I тысячелетия до Новой эры»), считает несомненным, «что древние математики достаточно хорошо владели методом логического доказательства математических истин» 92. И он не одинок, давая вавилонянам такую высокую оценку. Подобного же мнения придерживается и один из патриархов в этой области знания — О. Нейгебауер, который пишет, что «в исторических исследованиях слово «доказать» может иметь только тот смысл, что из тех или иных математических данных и зависимостей при помощи логических умозаключений выводятся новые математические зависимости. Трудно допустить что-либо другое, — продолжает он, — кроме следующего: вавилоняне приводили путём ряда последовательных умозаключений более сложный случай к более простым» 93. Получается, что вавилонские математики ничем не отличались от современных. Однако никаких рассуждений и умозаключений мы в текстах того периода не встречаем. Может быть, они не сохранились? Такое случается, но в данном случае дело в другом: похоже, математическое мышление, как его сегодня понимает наука, просто ещё не сложилось. Однако это требуется показать, пока же вернёмся к историческим реконструкциям. На что опираются историки математики, оценивая столь высоко вклад в науку шумеро-вавилонской математики? Прежде всего, на собственные реконструкции решений задач, сведения о которых даёт расшифровка тысяч и тысяч глиняных табличек, добытых археологами из-под развалин дворцов, хозяйственных построек и школ Древнего Шумера и Вавилона. В этих табличках приведены условия и решения огромного числа задач, но, увы, ничего не сказано о том, почему эти задачи решались именно так, а не иначе. Уже сам характер условий задач и способов их решения поразил и озадачил историков математики. Оказалось, что задачи подобного типа сегодня решаются с помощью алгебраических методов или же их арифметических и геометрических эквивалентов (специально построенных арифметических или геометрических уравнений и преобразований). Решение многих таких задач предполагает довольно развитые математические знания: нужно владеть способами преобразования одних уравнений в другие, знать решения квадратных (и даже кубических) алгебраических уравнений и, наконец, теорему Пифагора. И всё это при условии, что о геометрии или алгебре вавилонский математик ничего не знал, да и как он мог узнать, если эти математические дисциплины возникли одна примерно две тысячи, а другая три тысячи лет спустя. Приведём одно из условий вавилонской математической задачи и способ её решения. Условие: Длина и ширина. Длина превышает ширину на 4, площадь 32, узнай длину и ширину. Решение: 4 раздели пополам, получишь два. Два умножь на само себя, ты видишь площадь — 4. Площади 32 и 4 сложи, ты видишь 36. Узнай корень квадратный из 36. Это 6.6 и 2 сложи, ты видишь 8 — длина. От 6 отними 2, ты видишь 4 — ширина. Это решение, с точки зрения А. Ваймана, позволяет сделать вывод, что шумеры знали алгебраические формулы и преобразования, которые Вайман и приводит в своей книге 93. Как же решались эти задачи, на основе какого метода и счисления? Если бы у историков математики были сведения о способах решения вавилонских задач или стиле мышления вавилонских математиков, то методы решения этих задач можно было бы восстановить достаточно легко. Однако каждый крупный историк математики изобретает нечто заменяющее сведения о способах решения, а именно: на основе близких ему математических методов он реконструирует способы их решения. Анализ приёмов решения вавилонских задач заставляет думать, что они решались Здесь, естественно, возникает вопрос: как же так, ведь вавилонские математики не были знакомы ни с алгеброй, ни с геометрией, ни с современной теоретической арифметикой? Нельзя сказать, что историки математики не знают этого факта. Знают, и очень хорошо. Поэтому они говорят не прямо об алгебре, геометрии или теоретической арифметике, а о том, что, хотя древние математики и не знали этих математических дисциплин, они, тем не менее, «по сути» мыслили алгебраически, геометрически или арифметически. Вот, например, что пишет Вайман: «Наиболее правдоподобна гипотеза, которая может быть подкреплена некоторыми косвенными наблюдениями. Согласно этой гипотезе, по крайней мере, первоначально полные квадратные уравнения, как и система уравнений канонического вида, решались геометрически» 94. Иначе считают А. Ван дер Варден и О. Нейгебауер. «Вавилоняне, — пишет А. Ван дер Варден, — мыслили прежде всего алгебраически. Сквозь геометрическую внешность просвечивает алгебраическая сущность» 95. А вот высказывание Нейгебауера: «… эта математика имеет сильно выраженную алгебраическую ориентировку… вычисление ведётся с величайшим изяществом и совершенно тем же методом, который применили бы и мы теперь» 96. Но с мнением и реконструкцией Нейгебауера не согласен известный российский историк математики С. Я. Лурье. В комментариях к книге Нейгебауера он пишет: «От сложности применяемых Нейгебауером алгебраических формул рябит в глазах. По его мнению, вавилоняне применили вполне сознательно хитроумный алгебраический приём. Между тем если решить эту задачу тем арифметическим способом, который широко применялся в индийской и арабской математике и который скорее всего восходит к Вавилону, именно методом ложного предположения, то каждое из действий, применяемых в тексте, получит свой смысл и не окажется никакой нужды в нынешней алгебре». Два соображения об алгебраических и геометрических реконструкциях и о так называемом методе ложного предположения. Алгебраическая или геометрическая реконструкция вызывает сомнение уже хотя бы потому, что трудно предположить у вавилонских математиков наличие современного уровня и стиля математического мышления, а ведь именно это приходит на ум, если принять подобные реконструкции. Но, более того, оказывается, что вавилонские математики по уровню своего мышления стояли на голову выше современных математиков, которые без алгебраической или геометрической символики не могут решать вавилонские задачи, в то время как вавилоняне их решали даже в школах. Наконец, каким образом вавилонские математики пришли к алгебраическим или геометрическим методам решения и почему они не сделали ещё одного пустякового шага: не записали эти методы в стройной системе алгебраического и геометрического счисления? Сложнее оценить метод ложного предположения, на пер-вый взгляд, он вроде бы отвечает уровню вавилонского мышления 97. Но только на первый взгляд. Действительно, зачем, спрашивается, вместо одной задачи решать другую (подобный подход — сведение одной задачи к другим — естествен и оправдан в теоретическом мышлении и малопонятен в том случае, если оно ещё не сложилось). Кроме того, необходим моё условие применения метода ложного предположения — установление соотношений между задачей-моделью (ложным предположением) и исходной задачей, которую необходимо решить. Современные же логические и психолого-педагогические исследования показывают, что установить такие соотношения невозможно без моделирования условия задачи в алгебре или геометрии (вероятно, этот факт проверили на себе многие родители, безуспешно пытаясь в своё время помочь детям решить сложные арифметические задачи, не прибегая «по условиям игры» к алгебраическим уравнениям и преобразованиям). Следовательно, применение метода ложного предположения, как его реконструируют историки математики, в скрытом виде само предполагает обращение к алгебраическим или геометрическим соотношениям и преобразованиям. Итак, ни одна из реконструкций, предложенных историками математики, не выдерживает серьёзной критики. Спрашивается, почему? Возможно, потому, что создание хорошей реконструкции не под силу одним лишь историкам математики, знакомым, что естественно, главным образом с математикой. Ведь здесь речь идёт не столько о математике, сколько о мышлении, а мышление, как известно, изучается прежде всего, в логике, психологии, теории культуры. Наделяя вавилонских математиков современным стилем и характером мышления, историки математики нарушают, к примеру, некоторые основные принципы исторического рассмотрения культур, принципы исторического анализа человеческого сознания, мышления и поведения. Согласно этим принципам шумеро-вавилонская культура самобытна и непохожа на современную. Языки, сложившиеся в этой культуре (и математические в том числе), принципиально отличны от современных, мышление и поведение представителей шумеро-вавилонской культуры своеобразны и определяются всем строем данной культуры и её историей. Рассмотренная здесь ситуация с реконструкцией доантичных «математических» текстов сходна с ситуацией реконструкции древних «астрономических» текстов. С одной стороны, известно, например, что теоретическая астрономия сложилась только в Древней Греции (Евдокс, Гиппарх, Птоломей), с другой — О. Нейгебауер утверждает, что вавилоняне создали «стройную математическую теорию» движения Луны и планет 98. Впрочем, другие историки астрономии утверждают, что астрономия как наука сложилась только в античной культуре. Почему же историки науки по-разному объясняют начала и природу математики и астрономии и других точных наук? Хотя иногда различные реконструкции генезиса точных наук дополняют друг друга, всё же чаще они находятся, так сказать, в антагонистических отношениях. Естественное следствие подобного положения дел — борьба за истину, за правильный взгляд на исторический процесс, за поиски критериев предпочтения одного исторического объяснения другим. Один критерий предпочтения относительно очевиден. Новая историческая реконструкция и осмысление не дол-жны увеличивать противоречия в системе исторических знаний. Объясняя одно, нельзя запутывать весь круг проблем, порождать глубокие антиномии в существующем историческом предмете. Так, если принять, что вавилонские математики в Другой критерий предпочтения более сложен и менее очевиден. Почему иногда кто-то создаёт новую историческую реконструкцию, отказывается от существующих исторических знаний, критикует и зачёркивает их? Потому, что этот некто — носитель другой культуры мышления, представитель другого научного сообщества. Как правило, исторические реконструкции точных наук периодически обновляются и переписываются (перевоссоздаются) на основе современных гуманитарных способов научного мышления. Со всей определённостью нужно сказать: история — гуманитарная дисциплина со всеми вытекающими отсюда последствиями. Одной из важных особенностей гуманитарной науки является множественность точек зрения на один и тот же исторический материал, множество разных интерпретаций исторических текстов и фактов, разных исторических истин. Из введения и предыдущей главы должно быть ясно, что я буду осуществлять реконструкцию и строить объяснение в рамках культурологии. Теперь вторая проблема. Если предположить, что наука сложилась только в Античности, то всё равно нужно объяснить, каким образом в доантичной период получались новые знания и что это такое. Для меня как культуролога очевидно, что научное мышление в том виде, как мы его сегодня понимаем, то есть как получение знаний в рассуждениях и доказательствах, сложилось не раньше Античности. К тому же фактически до Мифологические знания имеют другое строение. Австралийские аборигены о человеке, лежащем в летаргическом сне и затем очнувшемся, говорят так: «Его душа отправилась к берегам реки смерти, но не была принята и вернулась оживить снова его тело» 99. Второй пример — рассмотренный в первой главе нарратив «жених-охотник». Третий, более развёрнутый — мифологические представления народов манси, живущих в Ханты-Мансийском автономном округе. Мифологическая система манси весьма сложная и богатая, местами напоминает верования персов, индусов, вавилонян, древних греков. Манси верят в духов (семейных, родовых, лесных, промысловых, добрых и злых), причём считают, что человек и животное имеют две души — ис («тень») и лили («дух»). Подругам этнографическим данным, мужчина имеет пять душ: душу, переходящую от одного человека к другому, душу-тень, душу-волосы, по которой человек после смерти идёт в мансийский рай, душу-дыхание и душу-тело. Женщина имеет четыре души. Верят манси также и в реинкарнацию, то есть переселение душ. Они считают, что в промежутке между смертью одного человека и рождением другого, в которого данная душа переселяется, для души нужно сделать специальное жилище, на-зываемое «иттермой». Как правило, иттерма представляет собой схематическое изображение умершего человека (в форме деревянного идола сантиметров 50–60, наряженного в расшитые бисером одежды). Раньше иттерма изготавливалась непременно из венца дома, где жил покойник. Манси считают, что душа покойного воплощается затем в младенца, родившегося в этом же доме 100. Спрашивается, можно ли считать все это знаниями и как представления манси объяснить с культурологической точки зрения. Обычно картины такого рода относят к мифам. Но на представления о реинкарнации, нарратив «жених-охотник» или понимание смерти как отбытия души в страну мёртвых можно посмотреть и с эпистемологической точки зрения, то есть как на мифологическое знание. Тогда возникают вопросы: что собой такие знания представляют, каким образом они были получены, с какой целью? Структуру самых простых, атрибутивных типов знаний: это «стол», «дерево», «олень», «большой», «зеленый», и тому подобное — проанализировал в своих ранних работах Г. П. Щедровицкий. Предварительным условием их формирования, показывает он, было выделение общественно фиксированных эталонов (например, эталона «олень» или «зеленый») и «изобретение» знаковой формы, то есть в данном случае соответствующих слов — «олень», «зеленый». Чтобы получить само знание А о некотором объекте X, пишет Щедровицкий, необходимо последний сопоставить с эталоном и, зафиксировав их тождество, выразить результат сопоставления в знаковой форме. Скажем, если объект Л’ удаётся отождествить с эталоном «олень», то этот объект называется словом «олень», хотя в содержании знака «олень», подчёркивал Щедровицкий, фиксируется и выражается прежде всего результат сопоставления объекта Хс эталоном 101. Более сложные типы знаний, вплоть до научных, Щедровицкий и участники ММК в конце Когда автор подключился в начале 2.2. Понятия «знак» и «схема»Объяснение происхождения мифологических знаний предполагает разведение указанных здесь понятий. Представление о знаке вводилось в ММК, чтобы объяснить, каким образом человек преодолевает ситуацию разрыва. Когда он по какой-либо причине не мог действовать с объектом, то изобретал знак, замещал объект знаком и действовал с последним вместо объекта. Именно по этой семиотической логике я смог объяснить природу и происхождение чисел Древнего мира, изображения людей и животных, использовавшиеся в доисторические времена охотниками для тренировки, и ряд других случаев. Попробовал я таким же образом (в середине С семиотической точки зрения душа это сложный тип знака, который можно назвать «знаком-выделения» 103. Его изобретение, как отмечалось выше, позволило архаическому человеку осмыслить (конституировать, поэтому знак «выделения») явления смерти, обморока, сновидений, появление зверей и людей, созданных с помощью рисунка. И не только осмыслить, но и, что не менее существенно, создать новые практики. Строение души как знака задаётся, с одной стороны, семантически (душа — это жизнь, то есть кто имеет душу, тот и живой; душа живёт в домике, откуда может выходить и куда может возвращаться; душа никогда не умирает), с другой — операциями. Первая операция с душой как знаком — уход навсегда души из тела; при отнесении к объекту (человеку, животному) эта операция осмысляется как смерть. На основе подобного понимания формируется и соответствующая архаическая практика — захоронение, понимаемая древним человеком как создание (постройка) для души нового дома. В этот дом (могилу), что известно из археологических раскопок, человек клал всё, что нужно было душе для продолжения на новом месте полноценной жизни: еду, оружие, утварь, одежду и так далее (позднее богатые люди могли позволить себе унести с собой в тот мир лошадей, рабов, даже любимую жену). Вторая операция — временный уход души из тела — осмыслялась как болезнь. На основе этой операции складывается архаическая практика врачевания (лечения), представляющая собой различные приёмы воздействия на душу (уговоры души, преподнесение ей подарков — жертвы, создание условий, которые она любит: тепло, холод, влажность, действие трав и так далее, — с целью заставить её вернуться в тело). Возвращение души в тело, понимаемое как «выздоровление», — это фактически обратная операция с душой как знаком по сравнению с прямой — временным уходом души. Древнее врачевание предполагало отслеживание и запоминание природных эффектов и комбинирование ряда практических действий, приводящих к таким эффектам. Другими словами, складывалась настоящая техника врачевания. Но, естественно, понималась она в рамках анимистического мироощущения. Третья операция — приход в тело человека во время сна другой души (или путешествие собственной души вне тела в период сна) — определила такое представление, как сновидение. Соответственно обратная операция задала смысл пробуждения, выхода из сновидения. На основе этого формируется практика толкования сновидений, понимаемая как свидетельства души. Четвёртая операция, точнее две группы операций, имеющих исключительно важное значение для архаической культуры, — это, во-первых, вызывание души, предъявление её зрению или слуху, во-вторых, обращение к душе, общение с ней, что достигалось с помощью средств древнего искусства (рисование, пение, игра на инструментах, изготовление масок и скульптурных фигур и так далее) В рамках этой практики формируется как специальная техника (например, изготовление музыкальных инструментов и масок, орудий и материалов для живописи и скульптуры), так и сложные технологии древнего искусства (рисование, танец, изготовление скульптур и так далее). Для нас естественно разделение живого и неживого, человека и природы. Для архаического человека живым было всё, что менялось, двигалось, от чего он зависел, что давало ему пищу или другие жизненные блага. Живой была земля (временами она содрогалась от землетрясений), она же дарила воду и пищу. Живым было небо, оно менялось, посылало дождь, гневалось громами и молниями. Живой была вода, она текла, бежала, умирала (испарялась), временами, во время наводнений, становилась страшной. Короче говоря, для архаического человека вся природа (планеты, солнце, луна, звезды, вода и земля, огонь и воздух, леса и озера) была живая. Но раз так, все природные стихии наделялись душой. Эти души назывались или собственно душами, или духами и демонами. Поясню теперь, как я пришёл к необходимости кроме знаков вводить понятие «семиотическая схема». Исследователь в любой науке, не только семиотике, нередко сталкивается со следующей методологической проблемой. С определённого момента он выходит на изучение таких явлений, которые уже плохо описываются и, главное, объясняются на основе наработанных представлений и понятий. Тогда учёный оказывается перед дилеммой — или продолжать двигаться в заданном направлении, стараясь всё же свести новые явления к уже изученным, принципиально не меняя основных понятий, или же создать новые понятия и идеальные объекты, проведя границу между одним классом явлений, описанных на основе исходных понятий, и другими, новыми классами, для изучения которых необходимы новые понятия. Третий вариант, близкий к первому, — создать такие понятия, которые бы описывали и объясняли широкую область, включающую разные классы явлений. Например, если судить по работам У. Эко, то очевидно, что он столкнулся с подобной методологической проблемой, когда пытался понять семиотическую природу иконическо-го знака, искусства, дизайна, архитектуры, рекламы. Разрешая эту ситуацию, Эко выбирает третий вариант. Он создаёт систему понятий, главными из которых являются понятия кода, риторики и идеологии (последние два задают для кода контексты), позволяющие описывать и объяснять все перечисленные явления. Однако при этом ему пришлось очень расширить понятие кода. Действительно, код, по Эко, — это то, что задаёт и систему константных общепризнанных значений, и систему локальных, частных значений (так называемый «лексикод»), и значения «произведения искусств» (Эко называет такой специфический код «идеолектом»), и «слабые коды», когда в зависимости от контекста и установок субъекта постоянно меняются значения; одновременно код понимается как семиотический метод анализа структур и как сама семиотическая структура, но часто и как структура восприятия 104. При таком расширительном понимании кода Эко вынужден постоянно фиксировать парадоксы. Например обсуждая идеолект произведения искусства, он пишет: «Так, произведение безостановочно преобразует денотации в коннотации, заставляя значения играть роль означающих новых означаемых. Тут-то и возникают две проблемы, которые можно рассматривать порознь, и в то же время они тесно связаны между собой:
И подобными парадоксами полна вся книга Эко. Не означает ли это, что столь расширительное понятие кода неоперативно и внутренне противоречиво? В своих семиотических исследованиях я тоже столкнулся с подобной же проблемой и примерно в тех же областях — семиотического объяснения искусства, науки, дизайна, сновидений, игры, общения, и тому подобного. Довольно долго я пытался реализовать первую стратегию, то есть сохранить в неизменности представления о знаках и их типах. Наконец, я понял, что эта стратегия семиотического исследования тупиковая. Решил выбрать второй вариант, то есть для семиотического объяснения перечисленных здесь явлений ввести новые семиотические понятия, а именно понятие схема. Примерами её являются схема метро, нарративные описания архаической души («Его душа отправилась к берегам реки смерти, но не была принята и вернулась оживить снова его тело») или схема анд-рогина (двуполого существа, которого Зевс рассек пополам) в платоновском «Пире». Прежде всего, следует обратить внимание, что схемы — это семиотические образования (они в своём материале представляют определённые предметы, отличные от них самих). Но схемы — это не отдельные знаки и даже не системы знаков, а самостоятельные семиотические предметы. Что объединяет знаки и схемы? Главным образом метод семиотической реконструкции, намеченный в ряде моих работ. Он включает в себя:
Ситуации разрыва рассматривались как причины формирования новых знаков. Витальные катастрофы автор ввел, чтобы объяснить становление новой культуры. Рассмотрим теперь специфические особенности схем. Известно, что у Канта в «Критике чистого разума» есть понятия «схематизма рассудка» и «схемы». Он пишет: «Это формальное и чистое условие чувственности, которым рассудочное понятие ограничивается в своём применении, мы будем называть схемой этого рассудочного понятия, а способ, которым рассудок обращается с этими схемами, — схематизмом чистого рассудка. Следовательно, схемы чистых понятий суть истинные и единственные условия, способные дать этим понятиям отношение к объектам, стало быть значение, и потому в конце концов категории не могут иметь никакого другого применения, кроме эмпирического, так как они служат лишь для того, чтобы посредством оснований a priori необходимого единства (ради необходимого объединения всего сознания в первоначальной апперцепции) подчинить явления общим правилам синтеза и таким образом сделать их пригодными для полного соединения в опыте» 107. Обратим внимание, с точки зрения Канта, именно схемы придают категориям и понятиям значение. Но одновременно в кантианской системе роль схем и схематизмов не столь уж и велика: как подчёркивает Кант, «схема есть, собственно, лишь феномен или чувственное понятие предмета, нахо-дящееся в соответствии с категорией», имеющей независимое от всякой схемы и гораздо более широкое значение. Другой интересный момент состоит в том, что хотя без схем мышление, по Канту, не может состояться, поскольку построить синтетическое суждение и получить в нём новое знание можно только при соотнесении априорных представлений с предметами опыта, тем не менее собственно логической характеристикой схемы не обладают, то есть к мышлению они прямо не относятся. В кантианской системе подобное неоднозначное, если не сказать отчасти противоречивое, понимание схем, вообще-то, понятно, но за пределами этой системы представления о схемах и схематизме мышления нуждаются в осмыслении, тем более что, действительно, без использования разного рода схем мышление невозможно. В современной методологии нередко можно услышать и утверждения (я их слышал, например, из уст Г. П. Щедровицкого и С. В. Попова) о том, что именно схемы, а не знания и понятия являются основными познавательными инструментами не только методологии, но и всех современных общественных и гуманитарных дисциплин. Однако даже и без таких сильных заявлений любой внимательный философ и учёный может заметить, сколь широкое применение имеют сегодня схемы. Интересный анализ происхождения и употребления схем в естественных науках мы встречаем в работах В. С. Стёпина, но он не рассматривал специально гносеологическую природу схем. Если же это делать, возникают вопросы. Чем являются схемы в познавательном отношении, по сути, ведь не ясно. Схемы — это не знания, хотя могут быть использованы для получения знаний (но каких?). Схемы сами по себе не являются объектами, однако часто задают объекты; именно в этом случае мы говорим об «онтологических схемах». Схемы — это и не понятия, хотя нередко именно со схем начинается жизнь понятий. Без схем современное мышление не могло бы состоятся, но после того, как оно «встает на ноги», часто исследователи вполне успешно могут обходиться без схем. Спрашивается, почему? И так далее и тому подобное, здесь что ни вопрос — удовлетворительного ответа на него нет. Все это говорит о том, что возникла настоятельная необходимость в анализе и осмыслении схем и схематизмов мышления. В качестве эмпирического материала я возьму два случая использования схем: один, очень ранний, донаучный — в знаменитом диалоге Платона «Пир», другой более поздний, как раз ближе к научному — в не менее известной работе Галилея «Беседы» (точное название: «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению»). В «Пире» мы находим несколько схем, которые я сначала перечислю. Во-первых, это схема двух Афродит. Один из участников диалога Павсий (а диалог формально посвящён прославлению бога любви) говорит, что нужно различать двух разных Эротов, богов любви, соответствующих двум Афродитам — Афродите простонародной (пошлой) и Афродите возвышенной (небесной), и что только последняя полна всяческих достоинств 108. Во-вторых, схема андрогина и его метаморфоз. Другой участник диалога Аристофан рассказывает историю, в соответствие с которой каждый мужчина и женщина ищут свою половину, поскольку они произошли от единого андрогинного существа, рассеченного Зевсом в доисторические времена на две половины 109. В-третьих, схема, описывающая путь людей, которые, как выражается Диотима, разрешаются в любви духовным бременем 110. Этих людей, противопоставляемых обычным возлюбленным, вполне можно назвать эзотериками, конечно, в платоновском понимании эзотеризма. Наконец, в-четвёртых, в «Пире» можно найти схему, в которой любви приписываются такие качества, как гармония, рассудительность, мудрость, даже стремление к бессмертию 111. Следует отметить, что перечисленные здесь образования в тексте Платона ниоткуда не выводятся, а, напротив, сами являются источниками рассуждений о любви и получения о ней знаний. При этом каждое такое образование представляет собой некую целостность в отношении последующих рассуждений о любви. Действительно, рассказывая историю с андрогином, Аристофан получает знание о том, что возлюбленным присуще стремление к поиску своей половины. Деление Афродит на вульгарную и возвышенную позволяет приписать любви мужнины к прекрасному юноше различные достоинства, а мужчине к женщине — только низменную страсть. Соответственно той же цели приписывания любви необычных (если сравнивать с распространённым, народным пониманием любви) качеств: совершенствования личности, работы над собой, стремления к бессмертию — служат рассуждения по поводу людей, разрешающихся в любви духовным бременем. Таким образом, с помощью схем герои диалога (а фактически сам Платон) получают различные знания о любви. Ещё один признак схем: как правило, они могут стать объектами оперирования, в том смысле, что схемы имеют определённое строение, их можно анализировать, на основе одних схем можно создавать другие, и тому подобное. Следующая наиболее важная особенность схем — они являются самостоятельными предметами, что осознается даже в этимологии этого термина (от греч. scema — наружный вид, форма). Предложим следующее рабочее определение схемы: схема — это самостоятельный предмет, выступающий одновременно как представление (или изображение) другого предмета. Понятно, что схема может быть использована и в функции модели (как известно, модель — это объект, употребляемый вместо другого объекта), но схема всё же не совпадает с моделью. Для схемы существенна именно предметность: схема и сама является самостоятельным предметом, и представляет другой предмет, это, так сказать, предмет в квадрате. В качестве первого предмета (корня) схема выступает как источник знаний, в качестве второго (самого квадрата) позволяет переносить знания с одного предмета на другой. Имеет смысл рассмотреть тот способ, на основе которого Платон получает на схемах новые знания. Рассмотрим для этого более подробно историю об андрогинах. Сначала рассказывается сама история, а именно то, как Зевс рассек андрогинов пополам. Затем половинки андроги-нов отождествляются с мужчинами и женщинами или с разными мужчинами. Наконец, влюблённым мужчинам и женщинам приписывается стремление к поиску своей половины, поскольку их происхождение от андрогинов требует воссоединения целого. Кант, вероятно, сказал бы, что категории «часть — целое», «любовь» и «пол» — это априорные начала, применение которых к реальным объектам (людям) и потребовало схемы андрогина. Платон рассуждает иначе: с помощью «правдоподобной» истории об андрогине душа вспоминает совершенную идею любви, которая создана творцом. А я вижу в рассуждении героя диалога нечто другое. Откуда, спрашивается, Платон извлекает новое знание о любви? Он не может изучать (созерцать) объект, ведь платонической любви в культуре ещё не было, а обычное понимание любви было прямо противоположно платоновскому. Платон утверждал, что любовь — это забота о себе каждого отдельного человека, а народное понимание языком мифа гласило, что любовь от человека не зависит (она возникает, когда Эрот поражает человека своей золотой стрелой); Платон приписывает любви разумное начало, а народ — только страсть; Платон рассматривает любовь как духовное занятие, а народ — преимущественно как телесное, и тому подобное. Новое знание Платон получает именно из схемы, очевидно, он её так и создаёт, чтобы получить такое знание. Но относит Платон это знание, предварительно модифицировав его (здесь и потребовалось отождествление), не к схеме, а к объекту рассуждения, в данном случае к любви. Возникает вопрос: на каких основаниях, ведь объекта ещё нет? Платон бы возразил: как это нет объекта, а идея любви, её творец создал одновременно с космосом, и душа созерцала совершенную любовь, когда пребывала в божественном мире. Но я не Платон и должен повторить. К моменту создания «Пира» платонической любви ещё не было. Следовательно, я могу предположить лишь одно: Платон полагает (современный инженер сказал бы «проектирует») новое представление о любви, и именно для этого ему нужна схема. Она задаёт, а не описывает новый объект; полученные на схеме знания приписываются этому объекту, конституируя его. То же самое можно утверждать и относительно других платоновских схем. Рассмотрим теперь второй пример — схемы в «Беседах» Галилея. Исследования В. Зубова показывают, что в основании всех поисков Галилея, позволивших ему получить новые знания о движении (свободном падении тела), лежит заимствованная им у средневекового логика Николая Орема «схема треугольника скоростей». В этой схеме один катет прямоугольного треугольника изображает пройдённое время, а другой — максимальную скорость, достигнутую при свободном падении тела (прямые внутри треугольника, параллельные этой максимальной скорости, — это мгновенные скорости в определённый момент времени падения). На оремовской схеме Галилей получает исходное знание о том, что скорость падающего тела увеличивается равномерно, которое он кладёт в основание всех дальнейших доказательств. «Поэтому, — пишет Галилей, — когда я замечаю, что камень, выведенный из состояния покоя и падающий со значительной высоты, приобретает все новое и новое приращение скорости, не должен ли я думать, что подобное приращение происходит в самой простой и ясной для всякого форме? Если внимательно всмотримся в дело, то найдём, что нет приращения более простого, чем происходящее всегда равномерно. К такому заключению мы придём, подумав о сродстве понятий времени и движения» 112. Отталкиваясь от той же схемы, Галилей получает ещё два знания: что все тела должны падать с одинаковой скоростью независимо от их веса и что вес тела расходуется не на поддержание движения, а только на его приращение (Аристотель утверждал обратное: скорость падения прямо пропорциональна весу падающего тела и для поддержания равномерного движения тела необходимо постоянно прикладывать определённую силу). Наконец, ещё одно знание («Если тело, выйдя из состояния покоя, падает равномерно ускоренно, то расстояния, проходимые им за определённые промежутки времени, относятся между собой, как квадраты времени») Галилей получает, доказывая геометрическим путём равенство треугольника скоростей «прямоугольнику скоростей», то есть равенство равноускоренного движения равномерному движению со средней скоростью падения 113. Первое исходное знание Галилей получает примерно так же, как Платон. Он доказывает, что предположение о равномерном приращении скорости падающего тела является наиболее естественным и соответствующим природе изучаемого явления. Другими словами, схема треугольника скоростей построена так, чтобы приписать падающему телу данное соотношение. По-другому получаются второе и третье знания. Почему, рассуждает Галилей (смотри нашу реконструкцию 114), нельзя считать, что вес тела тратится на поддержание его постоянной скорости. А потому, что в этом случае нельзя объяснить ускорение тела при падении, ведь тогда пришлось бы считать, что по мере падения и вес тела постоянно возрастает. Почему все тела падают с одинаковой скоростью независимо от их веса? А потому, что в треугольник скоростей входят только два параметра — скорость тела и пройдённое время, а параметр веса не входит, следовательно, от веса тела скорость не зависит. Как мы видим, новые знания здесь получаются не прямо из оремовской схемы, но в связи с ней. В данном случае схема помогает организовать соответствующие рассуждения. Наконец, четвёртое знание получается при отождествлении оремовской схемы с определённой геометрической фигурой. На основе полученного в геометрии знания о равенстве фигур далее создаётся новое знание о свободном падении. То есть новое знание здесь создаётся в два этапа: сначала в геометрии, затем в механике, но и там и там объекты задаются с помощью схемы треугольника скоростей. Если Платон в обосновании своих знаний апеллирует к идеям, то Галилей — к устройству природы как «написанной на языке математики». В частности, в «Диалоге о двух главных системах мира» Галилей пишет: «Но если человече-ское понимание рассматривается интенсивно и коль скоро под интенсивностью разумеют совершенное понимание некоторых суждений, то я говорю, что человеческий интеллект действительно понимает некоторые из этих суждений совершенно и что в них он приобретает ту же степень достоверности, какую имеет сама Природа. К этим суждениям принадлежат только математические науки, а именно геометрия и арифметика, в которых божественный интеллект действительно знает бесконечное число суждений, поскольку он знает всё. И что касается того немногого, что действительно понимает человеческий интеллект, то я считаю, что это знание равно божественному в его объективной достоверности, поскольку здесь человеку удаётся понять необходимость, выше которой не может быть никакой более высокой достоверности» 115. Вернёмся теперь к проблеме определения специфических характеристик схем. Обратим внимание на контекст, в котором Платон вводит схему андрогина. Этот контекст явно игровой, участники диалога берутся прославлять на пирушке бога любви Эрота, а Аристофан рассказывает историю, безусловно им лично сочинённую; во всяком случае, такого нарратива в стандартном наборе греческих мифов не было. Другими словами, отношения, устанавливаемые между выдуманной историей и отношениями возлюбленных, не являются общезначимыми, они устанавливаются тут же, в реальности беседы о любви. То есть в отличие от знака, имеющего константное общезначимое значение, схема как семиотическое образование условна, что часто и фиксируется в её определении. Значение схемы устанавливается относительно данного контекста и реальности, в других реальностях значение схемы может быть иным. Установленное в определённом контексте значение схемы, конечно, может сохраниться и в дальнейшем употреблении, как, например, это произошло со схемой метро или схемами архаической души. В этом, не столь уж редком случае схема, сохраняя свою функцию схемы, превращается в знак (иногда в символ, как в случае креста). Однако в общем случае специфическая особенность схем состоит именно в том, что их значения устанавливаются и имеют силу в рамках определённой реальности (игровой, познавательной, общения и так далее). Ещё одна важная характеристика схем — осознание её предметности. И знак может превращаться (и постоянно превращается) в предмет, но этот момент обычно не осознается, поскольку знак используется прежде всего как средство деятельности. Напротив, строение схемы, её предметные возможности интересуют создателя или пользователя схемы в первую очередь, поскольку именно они позволяют решить с помощью схемы определённую задачу, например, получить на схеме новое знание и отнести его к схематизируемому предмету. Чем ещё схемы отличаются от знаков? Говоря о знаках, мы употребляем два ключевых слова — «обозначение» и «замещение», например, некоторое число как знак обозначает то-то (скажем, совокупность предметов), замещает такой-то предмет (эту совокупность) в плане количества. У схемы другие ключевые слова — «описание» и «средство» (средство организации деятельности и понимания). Например, мы говорим, что схема метро описывает пересадки и маршруты движения, помогает понять, как человеку эффективно действовать в метрополитене. Знаки вводятся в ситуации, когда уже сформировалась некоторая объектная область, но по какой-либо причине человек не может действовать с объектами этой области (например, они разрушились, громоздки, и тому подобное). Замещая эти объекты знаками и действуя с ними вместо того, чтобы действовать с соответствующими объектами, человек получает возможность достигнуть нужного ему результата; при этом частично перестраивается и сама деятельность и Схемы тоже означают некоторую предметную область (например, схема архаической души — состояния человека), но эта их функция не главная, а подчинённая; можно сказать, что она вообще находится на другом иерархическом уровне. Более важны две другие функции: организации деятельности и понимания, выявление новой реальности. Здесь нет исходной объектной области, которая означается. Напротив, создаётся новая объектная и предметная область. До изобретения схемы души никаких душ не существовало. Схема вводится с целью организации новой деятельности, материалом которой выступают различные состояния человека, при этом душа — это не ещё одно интегральное состояние, а новая антропологическая реальность. Чтобы лучше понять этот тезис, рассмотрим более подробно, как могли сформироваться представления о душе в архаической культуре и языческих богах в культуре древних царств. Где-то на рубеже Не зная, как действовать в случаях смерти, заболевания, обморока, сновидений, встречи с изображениями животных или людей, вождь племени случайно отождествляет состояния птички (она может вылететь из гнезда, вернуться в него, навсегда его покинуть и так далее) с интересующими его состояниями человека (смертью, болезнью, выздоровлением, и тому подобное) и дальше использует возникшую связь состояний как руководство в своих действиях. Например, если человек долго не просыпается и перестал дышать, это значит, что его «птичка-дыхание» улетела из тела навсегда. Чтобы улетевшая «птичка-дыхание» не осталась без дома, ей надо сделать но-вый, куда можно отнести и бездыханное тело. Именно это вождь и приказывает делать остальным членам племени, то есть, с нашей точки зрения, хоронить умершего. Объясняя другим членам племени свои действия, вождь говорит, что у человека есть птичка-дыхание, которая живёт в его теле или улетает навсегда, но иногда может вернуться. Пытаясь понять сказанное и тем самым оправдать приказы вождя и собственные действия, члены племени вынуждены представить состояния человека как состояния птички, в результате они обнаруживают новую реальность — душу человека. Если у вождя склейка состояний птички и человека возникла случайно (например, ему приснился такой сон, или, рассказывая о птичке, покинувшей гнездо, он случайно назвал её именем умершего), то у членов племени, старающихся понять действия и слова вождя, эта склейка (означение) возникает в результате усилий понять сказанное вождём и осмыслить реальный результат новых действий. Необычные слова вождя, утверждающего, что у человека есть птичка-дыхание, помогают осуществить этот процесс понимания-осмысления. Подобные языковые конструкции и являются первыми схемами, они выполняют несколько функций: помогают понять происходящее, организуют деятельность человека, собирают смыслы, до этого никак не связанные между собой, способствуют выявлению новой реальности. Необходимым условием формирования схем является означение, то есть замещение в языке одних представлений другими (в данном случае необходимо было определённые состояния человека представить в качестве состояний птички-дыхания). Изобретя представление о душе, человек смог действовать во всех указанных выше случаях; более того, можно предположить, что выжили только те племена, которые пришли к представлению о душе. На основе анимистических представлений формируются и первые социальные практики (захоронения умерших, лечения, толкования сновидений, вызывания душ и общения с ними), а также соответствующее понимание и видение мира (он был населен душами, которые помогали или вредили человеку). 118 И опять именно схемы помогали человеку распростра-нить анимистические представления на новые случаи и ситуации. Например, как можно было понять, почему в семье и племени все люди похожи и связаны между собой? Двигаясь в схеме души: птичка могла переселиться из одного гнезда в другое, аналогично душа умершего могла вернуться в тело ребёнка, родившегося в данной семье (племени). Решая одни проблемы, архаический человек порождал другие, эти — третьи, и так до тех пор, пока не удавалось выйти на понимание реальности (мира), обеспечивающей при сложившихся условиях устойчивую социальную жизнь. Теперь вторая иллюстрация. Приглядимся к языческим богам Древнего Египта, Шумера, Вавилона, Древней Индии и Китая (по моей классификации, эти социальные образования относятся к культуре древних царств). В своих работах я старался показать, что главная их особенность в том, что они управляют человеком (обладают властью), любым, даже царём (фараоном). Другая особенность — каждая профессия и каждая специальность имела своего бога-покровителя. Наконец, ещё одно важное свойство языческих богов — они всегда действуют совместно с человеком. Сеет ли он зерно в поле, строит ли свой дом, зачинает ли собственного сына или дочь — всегда вместе с ним действуют соответствующие боги, которые направляют человека и помогают ему. Осмысляя перечисленные характеристики богов, я предположил, что боги — это мифологическое осознание (кон-ституирование) новой социальной реальности: разделения труда и систем управления (власти), соответственно отношения человека с богами выражали в мифологической форме участие человека в разделении труда и в систе-мах управления и власти. По механизму обнаружение реальности богов должно напоминать процесс, который привёл к представлению о душе. Только здесь для сборки разных смыслов и выявления новой реальности потребовались более сложные схемы — мифы о том, как боги создали мир и человека, пожертвовав для этой цели своей жизнью 119. В религиозной реальности допустимы одни события и совершенно исключаются другие. Например, бог может создать, всё, что пожелает, вселиться в кого или что угодно, может, даже обязан помогать человеку, если последний принёс ему жертву или отдал часть произведённого им продукта, функция бога — направлять человека, другая, как говорили шумеры, — «закрывать дорогу демонам» (вот где последние появляются, но это уже не души, приносящие несчастья, а настоящие злодейские существа, находящиеся в сложных отношениях как с людьми, так и с богами) и так далее. Однако в религиозной реальности недопустимы примат душ или духов (они, безусловно, должны подчиняться богам) или причинно-следственные связи, напоминающие природные естественные отношения. Думаю, рассмотренные два примера помогают лучше понять, что такое схема. Продолжим анализ общих характеристик схемы. Схему в силу её означающих возможностей можно использовать не только в собственной функции, но и как знак. Например, схему метро можно использовать не для организации нашего поведения в метрополитене, а как знак-модель, чтобы определить, по какому маршруту можно быстрее добраться от одной станции до другой. И то в данном случае эта задача может быть рассмотрена как аспект нашего поведения в метро. Ещё одна характеристика схем — на её основе создаётся возможность приписывать схематизируемой реальности новые свойства и связи. Действительно, сами по себе состоя-ния архаического человека (смерть, болезнь, и тому подобное) связаны одним образом, в практике и образе сложившейся жизни, но, схематизированные в представлении о душе, они организуются и связываются другим способом, по-новому. А именно через идею особой птички — обладателя жизни. Соответственно состояния падающего тела в опыте наблюдения за ним связаны одним образом, а представленные с помощью оремовского треугольника — совершенно другим. Геометрические свойства этого треугольника Галилей приписывает свободному паданию. Понятно, что эта последняя характеристика схем дополнительна к их характеристике задавать новую реальность. 2.3. Знание и нерефлексированное познаниеВ ранних работах Г. П. Щедровицкого была принципиальная неясность. С одной стороны, он трактует знание в контексте мыслительной деятельности, и тогда оно редуцируется (сводится) к знаку. С другой — сохраняется эпистемологическая трактовка знания; в этом случае знание характеризуется как структура формы и содержания (форма представляет содержание, содержание представлено в форме). Введя понятие знаковой формы, Г. Щедровицкий пытается удержать эпистемологичекую трактовку знания; настаивая на деятельностной природе мышления, он вынужден сводить знания к знакам, что в конце концов и произошло. Сегодня я решаю эту дилемму следующим образом. Знание не тождественно знаку (схеме). Семиотический процесс является операциональной несущей основой знания. Другими словами, чтобы получить знание, необходимы замещение, означение и действия со знаками или схемами. Но знание возникает как бы перпендикулярно, в сознании человека при условии своеобразного удвоения действительности. В сознании человека, получающего и понимающего знание, под влиянием требований коммуникации (например, необходимости при отсутствии предмета сообщить о нём другим членам общества) предмет начинает существовать двояко — и сам по себе, и как представленный в семиотической форме (слове, рисунке и так далее). Знание «слон» фиксирует не только представление о слоне, сложившееся в обычной практике, но и представление о слоне, неотделимое от слова «слон». В обычном сознании эти два представления сливаются в одно целое — знание, но в контексте общения (коммуникации) и деятельности они расходятся и выполняют разные функции. Так, именно второе представление позволяет транслировать знание и действовать с ним как с самостоятельным объектом, в то же время первое представление — необходимое условие формирования и опознания эталона. Указанное здесь представление о знании в той или иной форме осознавалось многими философами. Например, Аристотель фиксировал различие знания и объекта, причём содержание знания в его системе часто совпадает с сущностью объекта. Кант говорил о созерцании. «Каким бы образом и при помощи каких бы средств, — пишет Кант, — ни относилось познание к предметам, во всяком случае созерцание есть именно тот способ, каким познание непосредственно относится к ним и к которому как к средству стремится всякое мышление» 120. Почему мышление ставится в зависимость от созерцания? А потому, что в знании одно представление фиксируется (отражается) в другом. Мышление, рассматриваемое в качестве способа получения знаний, то есть познания, и определяется как способность отражения («описания») предмета, как созерцание. Другими словами, о знании мы говорим в контексте не только коммуникации, но и познания, для знака же познавательная деятельность необязательна. Вот почему я утверждаю, что знание хотя и возникает на семиотической основе, к знакам не сводится. Коммуника-ция, замещения, означения и другие действия со знаками создают в сознании условия для поляризации целостного представления о предмете: одно из них осознается как знание, второе — как объект знания или его содержание. В «Теории культуры» я показываю, что в социокультурной действительности необходимо различать два основных процесса — становления и функционирования. К первому относится разрешение витальных катастроф, формирование базисных культурных сценариев и картин мира, основных социальных институтов, хозяйства и экономики, системы власти, профессиональных сообществ и общества, ко второму процессу — распространение всех этих структур на новые ситуации в новых условиях, что, конечно, предполагает их усложнение и развитие, но не ведёт к принципиальному изменению самих этих структур. При этом генезис первых культур позволил выделить в отдельной культуре базисные представления (например, о душе человека для архаической культуры, о богах для культуры древних царств), которые являются центральными и сохраняются в течение жизни культуры. Эти представления я и назвал «базисными культурными сценариями» 121. Генезис культур показывает, что под влиянием базисных культурных сценариев складываются и другие основные составляющие культуры (социальные институты, власть, общество, личность, сообщества). Например, для культуры древних царств — это армия, жреческая и царская власть, хозяйство, образование, судопроизводство. Выполняя в социальном организме определённые функции (внешние или внутренние — защиты, управления, производства, воспроизводства, разрешения конфликтов), социальные институты одновременно строятся так, чтобы соответствовать базисным культурным сценариям. Например, армия в культуре древних царств возглавлялась не только полководцами, но и богами войны и народа, поэтому на неё распространялись все основные сакральные сценарии (необходимость жертвоприношений, уяснение воли и указаний богов, ориентировка в сложных отношениях между главными богами, а по сути — в отношениях с другими институтами). Общество и сообщества, а позднее (в античной культуре) личность тоже складываются в культуре под влиянием базисных культурных сценариев. Например, общество и сообщества культуры древних царств консолидировались, структурировались и действовали от имени соответствующих богов (каждая община и каждое сообщество имело своего бога-покровителя, и, когда вырабатывалось коллективное решение, его идея и побудительный мотив приписывались богам). Наконец, и структура власти в культуре, понимаемая автором как инстанция, связывающая людей с системой социального управления, существенно обусловлена базисным культурным сценарием 122. В свою очередь, базисные культурные сценарии формируются как семиотические схемы при разрешении «витальных катастроф», то есть комплекса проблем, без решения которых новая культура как форма социальной жизни не могла бы сложиться (если понятие ситуации разрыва позволяет объяснить развитие деятельности, то витальной катастрофы — становление новой культуры). В становящейся культуре схемы как семиотические образования выполняют две важные функции: обеспечивают организацию деятельности и задают новую социальную реальность. Но и, обратно, социальная организация складывается именно при изобретении схем. Одновременно она есть необходимое условие становления культуры: в рамках социальной организации формируются социальные институты и другие социальные образования, например те же власть, общество, сообщества, личность. Таким образом, в каждой культуре складывается своё представление о мире, обусловленное существующими базисными сценариями, социальными институтами, структурой хозяйства и экономики, системой власти, обществом, популяциями. В периоды становления социокультурной действительности можно говорить и о становлении мира, в периоды функционирования — о его существовании. Именно на стадии существования мира появляется познание. Оно представляет собой семиотическое и схемное осмысление и освоение первой природы и самой социальной действительности в рамках сложившихся базисных сценариев. Например, в архаической культуре и первая, и вторая природы были поняты анимистически: земля, солнце, ветер, река и все остальные стихии — это были души, но точно так же племя, в котором жил человек, понималось как сообщество душ, переходящих от умерших к родившимся. Подобное осмысление представляло собой первый в истории человечества тип познания. Его особенностью было то, что сам процесс познания не осознавался, поэтому такой тип познания можно назвать нерефлексированным. Рассмотрим, например, как на схеме архаической души, задававшей базисный культурный сценарий архаической культуры, могло быть получено новое мифологическое знание о том, что после смерти родственников их души возвращаются в тела детей, родившихся в данной семье. Получению этого знания, вероятно, предшествовали следующие наблюдения (их можно трактовать как атрибутивные знания), полученные в разных бытийственных ситуациях, но почему-либо соединённых вместе. Первое — родственники в семье похожи друг на друга, не исключая умерших и живущих. Последнее могло звучать примерно так: «Умерший дед (бабушка, отец) вернулся, то есть снова родился». Второе — птица может сменить своё гнездо, перелетев из одного в другое. Совмещение обоих наблюдений на фоне актуализации представления о душе-птице создаёт условие для склейки в сознании двух образов — похожих друг на друга родственников и птицы-души, перелетающей из одного гнезда-дома (тела) в другой. Можно предположить, что подобная склейка облегчалась языковой игрой, воображением, сновидениями и стремлением понять возникший из соединения двух предметов феномен. Рождается же из всего этого новая схема (реинкарнации) и знание: «Живущие и умершие родственники имеют общие души». Кстати, в этом же контексте, вероятно, рождается и схема «древа жизни»: душа-птица, прежде чем влететь в новое гнездо, отдыхает на древе (жизни). На некоторых петроглифах так и изображено. В культуре древних царств и первая природа, и социальная жизнь осмыслялись в религиозном ключе: не только все природные стихии понимались как соответствующие боги (боги рек, бог солнца, богиня луны, боги земли и неба и так далее), но и социальные явления, например, в Шумере почитались боги государства, боги городов, боги кварталов, боги всех основных профессий. Частично начал осознаваться в той же религиозной форме и сам процесс познания. Действительно, чтобы согласовать деятельность человека с деятельностью и жизнью богов, жрецы стали вести регулярные наблюдения за поведением богов, то есть изучать движение солнца, луны, звёзд, начало и окончание разлива рек, и тому подобное, включая наблюдения за отдельными социальными явлениями, например гибелью одних царств и возникновением других. При этом жрецы, вероятно, не могли не осознавать в Аналогично можно показать, что элементы науки и астрономии были созданы (изобретены) вавилонянами и египтянами, когда они искали способы восстановления нарушенного с их точки зрения миропорядка. Геометрия, например, была изобретена, когда нужно было восстанавливать границы полей, смываемых каждый год Нилом и Ефратом 123. И как ещё, как не катастрофу, мог шумер понимать такой разлив: вода унесла межевые камни, какой теперь брать налог — неизвестно, а если налог не будет вовремя получен, боги разгневаются и отвернутся от человека, да и сама жизнь будет под угрозой. Но рассмотрим подробнее, как, например, сложился алгоритм вычисления прямоугольного поля. Итак, поскольку разливы рек смывали границы полей, перед древними народами каждый год вставала задача — восстанавливать границы, при этом необходимо, чтобы каждый земледелец получил ровно столько земли, сколько он имел до разлива реки. Судя по археологическим данным и сохранившимся названиям мер площади, данная проблема частично была разрешена, когда «размер» каждого поля стали фиксировать не только границами, но и тем количеством зерна, которое шло на засев поля. Действительно, наиболее древняя мера площади у всех древних народов — «зерно» — совпадает с мерой веса, имеющей то же название. Однако восстановление полей с помощью зерна не всегда было возможным или удобным: часто необходимо было восстановить поле, не засеивая его, засеять можно было по-разному, получив больше или меньше площади, и так далее. Эмпирический материал подсказывает, что был изобретён новый способ восстановления полей: теперь для восстановления прямоугольного поля у, равного по величине полю х, подсчитывали количество оставленных плугом в поле гряд (их толщина была стандартной), а также длину одной из гряд. В языке древних народов «гряда» — это не только название части поля, но и мера площади. Введение эталонной гряды, подсчёт количества гряд и их длины тоже не разрешали всех затруднений, поскольку в древнем земледелии постоянно приходилось решать задачи на сравнение по величине двух и более полей. Предположим, имеются два поля, которые надо сравнить. В первом поле 25 гряд, и каждая гряда имеет протяжённость 30 шагов, а в другом — 50 гряд протяжённостью в 20 шагов. Спрашивается, какое поле больше и насколько? Сделать это, сравнивая числа, невозможно: у первого поля большая протяжённость гряды, но в то же время меньше гряд. Однако поля можно сравнить по величине, если у них или одинаковое количество гряд, или одинаковая протяжённость (длина) гряды. Именно к этой ситуации старались прийти древние писцы и землемеры. Заметив, сравнивая урожаи полей, что величина поля не изменится, если длину гряды (количество гряд) увеличить в п раз и соответственно количество гряд (длину гряды) уменьшить в п раз, они стали преобразовывать поля, но не реально, а в плоскости замещающих их знаков (чисел). Например, чтобы решить приведённую здесь задачу, нужно количество гряд в первом поле увеличить в два раза (25 × 2 = 50), а длину гряды соответственно уменьшить в два раза (30 : 2 = 15). Так как в древнем мире обычно сравнивали большое количество полей разной величины (например, в Древнем Вавилоне сразу сравнивали несколько сотен полей), то постепенно сложилась практика приведения длины гряды к самой маленькой длине полей и в конце концов к единице длины (один шаг, локоть). Соответственно, чтобы не изменилась величина поля, количество гряд умножали на длину полей. Например, для полей, величина которых выражается числами 10, 40, 5, 25, 15, 20, 2, 30, получалась следующая таблица:
Поскольку слева всегда получается число 1, то величина поля выражается только числами и операциями в правом столбце, то есть произведением длины гряды на количество гряд. Естественно предположить, что этот факт рано или поздно был осознан древними писцами, они стали опускать числа 1 левого столбца и построили принципиально новый способ: сначала измеряли количество гряд и длину средней гряды (у прямоугольного поля — это любая гряда, у трапецеидального и треугольного — среднее арифметическое самой большой и самой маленькой длины), а затем вычисляли величину поля, перемножив полученные числа 124. Но если бы, например, шумерскому писцу, впервые нашедшему формулу вычисления площади прямого поля, сказали, что он На основе сложившихся по той же логике алгоритмов вычисления площадей полей, а также решения задач, связанных с суммированием и разделом полей, формируются и более сложные способы вычисления, включая приведённые выше «уравнения». На самом деле, как следует из реконструкции, это никакие не уравнения, а способы оперирования со сложившимися алгоритмами. Чтобы убедиться в этом, посмотрим «методом проникновения» в чужую культуру, как мог вавилонский «математик», а точнее, старший писец и распорядитель хозяйственных работ, он же часто и учитель, решать подобные «уравнения». Однажды в Древнем Шумере или Вавилоне к вавилонскому писцу, учителю и математику пришли люди и, поклонившись, говорят: «Ты искусный и мудрый писец, имя твоё славится, помоги нам поскорей. Два поля земли было у нас, одно превышало другое на 20 гар, об этом свидетельствует младший писец, бравший с нас налог, остальное он забыл. Прошлой ночью разлив реки смыл межевые камни и уничтожил границу между полями. Сосчитай же скорей, каковы наши поля, ведь общая их площадь известна — 60 гар». Выслушав людей, писец стал размышлять. Таких задач он никогда не решал. Он умел измерять поля, вычислять площади полей, если даны их элементы (ширина, длина, линия раздела), умел делить поля на части, соединять несколько полей между собой и даже узнавать сторону квадратного поля, если была известна его площадь. Он имел дело с тысячами таких задач, обучал в школе их решению и так хорошо знал своё дело, что перед его глазами как живые стоят глиняные таблички с решениями задач, чертежами полей и числами, проставленными на этих чертежах. Такие таблички он, старший писец и учитель, составляет каждое утро и даёт переписывать своим ученикам. Но среди табличек нет такой, которая бы помогла ему сейчас. Писец хотел было уже отослать людей, как вдруг вспомнил о задачах, которые он задал на табличках в прошлую неделю. Эти задачи были похожи на то, о чём ему говорили пришедшие люди. Перед глазами писца возникли чертежи с числами и решения. Первая задача:Поле в 60 гар (как раз по величине, которое возникло после разлива) разделили пополам. Узнай каждое поле. Решение: 60 : 2 = 30. Вторая задача:Поле 30 гар и другое 30 гар. От первого поля отрезали участок, равный 5 гар, и прибавили его к другому полю. Узнай получившиеся поля. Решение: 30 — 5 = 25; 30 + 5 = 35. Третья задача:Два поля 35 гар и 25 гар. На сколько одно поле выступает над другим. Решение: 35 — 25 = 10. Четвёртая задача:Два поля 35 гар и 25 гар соединили, узнай получившееся поле. Решение: 35 + 25 = 60. Писец вспомнил, что, решая сам эти задачи, он удивился, почему разница между полями — 10 гар — оказалась в два раза больше величины отрезанного от одного поля участка. И только посмотрев на чертеж, он понял, что эта разница суть удвоенный участок (от одного поля он отрезан, это 5 гар, а к другому прибавлен, ещё 5 гар, вместе же как раз 10 гар). Как похожи эти задачи на то, что произошло у людей, стоящих перед ним. Правда, разница между полями не 10 гар, а 20, но ведь это неважно, всё равно эта разница в два раза больше величины добавленного участка. И тут писца осенило. Мысленно воздал он почести великой лунной богине Иштар, подавшей ему знак, что делать: нужно разделить 60 гар пополам (как в той задаче, где поля были равные), а затем отнять от одного полученного при делении поля участок, равный половине 20 гар, и прибавить его к другому полю. И писец стал записывать решение первой в истории Вавилона задачи нового типа, не прибегая ни к алгебре, ни к геометрии, ни к методу ложного предположения 125. Безусловно, эта история выдумана с начала до конца, и, конечно, это очередная реконструкция, но обратите внимание на её достоинства. Я не ссылался на возможности современной математики и всё, что предположил, могу документально подтвердить и обосновать. Все перечисленные задачи действительно решались на определённом этапе развития вавилонской математики, решались тысячами, тиражировались тысячами тысяч в школах писцов, причём в разнообразных последовательностях и сочетаниях. Среди таких последовательно решённых (как правило, в учебных целях) задач при огромном потоке решений вполне могли встречаться и такие подборки задач, которые обеспечивали построение решений новых задач. Чертежи с числами и алгоритмы решений учебных задач (случайно, а в дальнейшем специально подобранные) облегчали отождествление уже решённых задач с условиями новых. Вот, например, как таким способом могла быть решена задача ещё одного типа, а также построена таблица пифагорейских троек (чисел 3, 4, 5; 5, 12, 13; 8, 15, 17 и так далее, для которых была справедлива теорема Пифагора) 126. Решение следующей задачи («Длина и ширина. Длина превышает ширину (высоту) на 4, площадь 32, узнай длину и ширину») могло быть найдено при сопоставлении следующей группы предварительно решённых задач. Прямоугольное поле. Высота 7. Длина 9. От поля отрезали вертикальный участок со стороной 1 и добавили горизонтальный участок со стороной 1. Какова величина (площадь) исходного поля и разница между площадями полей?
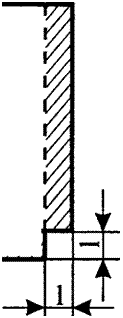
Решение 1: 1 × 9 = 63 (площадь исходного поля). Решение 2: 7 + 1 = 8; 9 — 1 = 8. Решение 3: 8 × 8 = 64 (площадь нового поля). Решение 4: 64 — 63 = 1 (разница между площадями полей). Рассматривая решения этих задач, можно заметить, что новое поле, возникшее после передела, — квадратное (8 × 8). Кроме того, разница между площадями полей (1) совпадает по величине с площадью, маленького квадратного поля (1 × 1), получившегося в правом нижнем углу чертежа. Наконец, высота и длина исходного и нового полей связаны следующими соотношениями: высота исходного поля меньше высоты нового квадратного поля на 1, а длина исходного поля больше длины нового поля на 1, разница же между длиной и высотой исходного поля (9 — 7 = 2) ровно в два раза больше стороны маленького квадратного поля (1). Отсюда при желании можно извлечь и план решения. Известна площадь исходного поля. Каким образом его нужно переделить, чтобы возникло новое квадратное поле? К исходному полю нужно добавить маленькое квадратное поле, сторона которого в два раза меньше разницы между длиной и высотой исходного поля. Затем нужно узнать сторону получившегося квадратного поля (то есть извлечь корень квадратный из площади этого поля) и добавить (отнять) к (от) этой стороне половину разности между длиной и высотой исходного поля. А вот серия задач, ведущих к пифагорейским тройкам. 1.Квадратное поле имеет площадь 16. От поля разлив отрезал треугольное поле со сторонами 3, 4, 5. На большей стороне треугольного поля построили квадратное поле. Определи площади отрезанного и построенного полей, а также разницу между площадями построенного и исходного полей. Решение 1: 5 × 5 = 25 (площадь построенного поля). Решение 2: (3 × 4) / 2 = 6 (площадь треугольного поля). Решение 3: 25 — 16 = 9 (разница между площадями). 2.Квадратное поле имеет площадь 16. К этому полю добавили ещё одно квадратное поле площадью 9. Узнай сторону первого и второго полей и сумму площадей обоих полей. Решение 1: 16 = 4 × 4. Решение 2: 9 = 3 × 3. Решение 3: 16 + 9 = 25. Анализ решений этих задач показывает, что площадь квадратного поля (25), построенного на большей стороне треугольного поля, равна сумме площадей исходного квадратного поля (16) и квадратного поля, построенного на меньшей стороне треугольника (9). Вавилонские математики скоро обнаружили, что не любое треугольное поле, отрезанное разливом, даёт такое замечательное отношение чисел (квадратов). Например, если размеры смытого треугольного поля будут 4, 2, 6, то квадрат, восстановленный на большей стороне треугольного поля, не будет равен сумме квадратов, построенных на двух других сторонах. Именно поэтому вавилонские математики стали создавать таблицы треугольных полей, размеры которых удовлетворяли открытому соотношению квадратов (3,4, 5; 5, 12, 13 и так далее). Предложенная здесь реконструкция заставляет пересмотреть многие представления о характере шумеро-вави-лонской математики. Во-первых, получается, что вавилонские математики пользовались вполне естественным (если иметь в виду уровень развития их практики) языком, который образовывали простейшие алгоритмы вычисления полей и поясняющие их чертежи с числами. Во-вторых, никаких уравнений они не знали и тем более не знали способов их преобразования. В-третьих, создавая решения задач, вавилонские математики не проводили логических умозаключений; всё, что от них требовалось в плане мышления, — сравнить между собой условие новой задачи с решениями специально или случайно подобранных задач. Конечно, это сравнение не было простым, оно включало в себя, с одной стороны, сравнение чертежей полей, с другой — сравнение чисел, фиксирующих размеры полей или их элементов. Кроме того, необходимо было путём вычислений связывать те или иные элементы полей или величины их площадей (например, деля одну величину на другую, выяснить, что одно поле в два раза больше другого). Однако все эти мыслительные действия ничего общего не имеют как с геометрическими или алгебраическими преобразованиями уравнений, так и с логическими умозаключениями. И Новые знания в Древнем мире получались не в рассуждениях, а на схемах. Действуя со схемами как со «знаковыми объектами», человек Древнего мира мог получить новые знания, например, что «души умерших переселяются в тела родившихся», «когда боги покидают человека, его дела идут плохо», «чтобы получить размер косого (треугольного) поля, нужно прямое поле (прямоугольное) разделить пополам» и другие. Эти знания проверялись на прочность в коллективном опыте социальной жизни, осмыслялись же они не рационально, а сакрально, то есть считались принадлежностью духов или богов, которые почему-либо поделились знаниями с людьми. Важно также понять, что нерефлексированное познание действительности — это, конечно же, наша современная реконструкция, а не древние представления. Мир не мыслился в те времена как объективно существующая сущность, которую нужно отобразить в знании. Духи и боги находились с людьми в сложных, если можно так выразиться, человеческих отношениях (поддерживали людей или нет, могли на них разгневаться, наслать кару и тому подобное). В лучшем случае человек мог стремиться узнать волю и намерение сакральных существ. Другое дело моя реконструкция, ориентированная на объяснение науки, её происхождение и типологию. В её рамках я утверждаю, что представления древних можно истолковать как схемы и их знаниевые описания. Хотя формулируют эти схемы и знания отдельные люди (шаманы, жрецы, писцы), не они выступают субъектом творчества, а в целом все древнее общество и культура. Чтобы новое знание закрепилось в культуре, оно должно было пройти проверку социальным опытом, и длилось это, как уже отмечалось, иногда сотни лет. Именно поэтому источником знаний считались духи и боги, а не люди. |
||||||||||||||||||