|
Направление движения предприятия с его сосредоточенностью скорее на том, к чему мы стремимся, чем на том, откуда мы вышли, или, иными словами, дальновидность — функция «думающей» части всей организации. В организме человека оценкой будущего занята кора головного мозга, на фирме — её высшее руководство. Можно спросить, как организована система для выработки политики и для принятия решений.
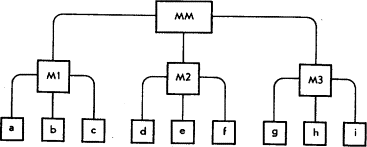
На Рис. № 39 представлена типичная организационная схема высшего звена управления фирмой. Здесь MM — управляющий всем предприятием — ответственный руководитель. У него три главных подчинённых, M1, M2 и M3, — директора или вице-президенты. У каждого из них по три подчинённых руководителя (так принято здесь просто для наглядности), а всего в данном примере 13 человек. Опытные бизнесмены скажут, что эта схема предназначена для того, чтобы показать организацию цепей руководства или, иначе говоря, распределение подотчётности. Никто из них не ожидает, что эта схема демонстрирует, как в действительности работает высший эшелон. И всё же верно, что некоторые предприятия реально действуют в соответствии с этой схемой, и так или иначе, в большей или меньшей степени, она влияет на их поведение. Попробуем рассмотреть подготовку весьма серьёзного решения, требующего ответа «да» или «нет» от ответственного руководителя, и влияние нашей схемы на его «правильное» поведение. Руководитель ММ вызывает подчинённых M1, M2 и M3 и объясняет им ситуацию. Он заявляет, что каждый из них должен придти к нему и доложить свои предложения независимо, а он сам примет общее решение. Это звучит разумно, поскольку если они соберутся сами и придут к нему с согласованным предложением, то зачем нужен ответственный руководитель? Он едва ли сможет что-либо противопоставить их общему мнению. Руководитель M1 уходит и вызывает к себе а, b, с. Они, конечно, руководители подчинённых ему подразделений, и он повторяет им точно то же, что сказал ему ответственный руководитель ММ. На том же основании М просит подчинённых не «нападать всей шайкой», поскольку он предпочитает выслушивать независимое мнение каждого и самостоятельно взвесить их доводы. В конечном счёте, руководитель a придёт со своим мнением к M1, как и все другие… Протокол выполняется точно. Все это звучит разумно и нормально. Возникает соблазн заметить, что дело идёт о весьма дисциплинированной компании, не подверженной обычному влиянию слухов и внутренних трений, которые (даже на самом верхнем уровне), Здесь всё ясно, формально все ведёт себя так, что кажется всё сработает удачно. Как представляется, всё идёт последовательно в хорошо руководимой организации, но при этом полностью игнорируется тот факт, что все люди не без греха. Возьмём a. Я уверен, что он сделал всё, что в его силах, чтобы дать правильный совет, и с этой целью консультировался со своими подчинёнными, а они, в свою очередь, со своими. Но прежде всего a, строго говоря (хотя на должностной лестнице стоит лишь на две ступени ниже ответственного руководителя — управляющего всей компанией), знает всего одну девятую общей картины. Более того, его подчинённые — разношерстная команда. Некоторые из них труженики, честные люди, но по крайней мере двое ничего не понимают в данном вопросе, но a не придаёт этому значения. Другой, самый напористый и демагог, прежде всего озабочен собственными амбициями — высадить a из кресла и занять его должность. Кроме того, все подчинённые a склонны ошибаться, даже самые честные из них, думающие и ответственные за свои советы. Так происходит потому, что все руководители испытывают трудности при управлении и подчинёнными им коллективами. Теперь какова цена совету a, который он дал M1, и как её измерять? Конечно, совет a не стоит высшей оценки, хотя схема организации каким-то образом поддерживает подобное мнение. Можно измерить ценность его совета на ряде подобных случаев, спросив, как часто совет, данный a, оказывался удовлетворительным (то есть точным, зрелым, хорошо взвешенным, перспективным, глубоким, учитывал интересы работников и так далее). Некоторые из читателей могут считать, исходя из этих критериев, что они никогда не получали удовлетворительного совета. Но нам не следует быть слишком строгими по отношению к нашим подчинённым, и я склонен предполагать, что полученные советы, в особенности на высшем уровне, значительно чаще оказывались правильными, чем наоборот. Например, можно сказать, что a дал хороший совет семь раз из десяти. Конечно, это хороший балл. И безусловно, так же можно подойти к оценке самого M1. Будем, однако, снисходительны и к нему. Поскольку он руководитель более высокого ранга, сочтём, что он на месте и предлагал ММ хорошие советы, правильные в восьми случаях из десяти. Сам MM, хотя они и ответственный руководитель, тоже может ошибаться. Но поскольку он на вершине, давайте будем считать, что он был прав в девяти случаях из десяти. Всё это, как можно полагать, весьма милосердно. Теперь попытаемся применить весь этот сценарий к частному примеру. Нужный ответ, который должен дать ответственный руководитель, — «да» (это мы знаем по прошлому). В данном случае «да» — правильный ответ. Если a прав в семи случаях из десяти, то вероятность его правильного ответа составит 0,7 и в этом случае. Такова же вероятность для b и с. Поскольку руководитель M1 запретил им обсуждать свои соображения с другими, их советы независимы. Пусть M1 человек осторожный, а дело (по его мнению) на этот раз настолько серьёзно, что он решил для себя сказать «да», только если «да» скажут все его подчинённые: а, b, с. Критерий принятия решения, тайно принятый M1, требует, чтобы все трое его подчинённых независимо друг от друга одновременно были правы. Вероятность того, что так случится, подсчитывается как 0,7 × 0,7 × 0,7. Согласно общему условию и личному решению M1 вероятность получить правильный совет составляет тогда 0,343. Предположим теперь, что M1 узнал, что в сказал не то, что думал на самом деле. Как мы знаем, сам M1 прав только в 80 процентах случаев. Теперь, если M1 передаёт ММ своё суждение как правильное, его вероятность правильности совета составит 0,8 × 0,343, то есть не более 0,2744. (Вот к чему приведут правила и осторожность!) Теперь М2 и M3 в отдельности проделают то же самое с такой же вероятностью на успех. Таким образом, с точки зрения ответственного управляющего — ММ, после того, как он по одному встретился со своими тремя заместителями, вся ситуация (которую он также проиграл «корректно» и благоразумно) становится довольно трудной. Хотите верьте, хотите нет, но он тоже решил не одобрять предложенный план, если все его заместители, M1, M2 и M3, не скажут «да». Вероятность того, что все три человека независимо поддержат план, не больше, чем ранее определённая вероятность в кубе, то есть всего 0,02. И, конечно, хотя он и ответственный, он тоже может ошибаться в 10 процентах, относительно получаемых им ответов. Следовательно, окончательная достоверность его решения, может быть найдена перемножением вероятностей принятия совместно руководителями M1, M2 и M3 верного решения (0,2) и его собственного успешного решения [0,9]. Таким образом вероятность того, что ММ в конце концов окажется прав — получается равной 0,018. Следовательно, результат для фирмы этой кажущейся столь замечательной и спокойной процедуры таков: главный управляющий принимает менее двух правильных решений из каждой сотни. Справедливо, что я несколько исказил пример, заявив «примем заранее ответ, да за правильный». Если бы мы этого не знали, то могли бы сказать, что ММ не стал бы с лёгкостью поддерживать такую громоздкую процедуру, которая выглядит куда более деликатной. Но даже в подобном случае щепетильность в таком масштабе смешна. Очевидно, что предприятия, действующие таким образом, погибли бы. Очевидно также, что фирмы в действительности не могут так организовать свою деятельность, Во-первых, многие дендриты (нервные процессоры, присоединяющиеся к нейронам как каналы ввода) иссякают Таким образом, мозг, если говорить об управляющих нейронах, во много раз хуже фирмы. Однако мозг работает. Употребив большое количество алкоголя, люди не теряют до конца своей способности вести себя по-человечески. Хотя у старика может сохраняться не более двух третей первоначального набора нейронов, его труд полностью оплачивают до конца службы (хотя и наблюдаются некоторые связанные с этим признаки старости). Фактически мозг решает свои проблемы точно так, как их решает фирма. Нейроны работают не независимо, а подкрепляют, усиливают работу друг друга. Управляющие в действительности тоже не изолированы друг от друга, как это могло бы следовать из организационной схемы фирмы. Короче говоря, система 5 является не набором узлов, а логически организованной и хорошо укомплектованной знающими людьми, как предполагалось нашей первой моделью. Эта система представляет собой искусно составленную взаимосвязанную сборку элементов, независимо от того, состоит ли она из нейронов или управляющих. Я назвал её «мультинодом» (многоузловой системой). Теперь, используя все эти представления, попытаемся начертить схему организации, лучшую, чем представлена на Рис. № 39. Результат такой попытки приведён на Рис. № 40, и тут сразу же каждый, кто когда-либо видел атлас мозга, заметит, что эта схема (за исключением буквенных обозначений) очень похожа на часть коры головного мозга. Фактически теперь мы восстанавливаем нашу модель нервной системы со значительно большей степенью детализации, чем раньше, и переходим от рассмотрения нейрофизиологии к нейроцитологии (цитология — наука, изучающая деятельность клеток).
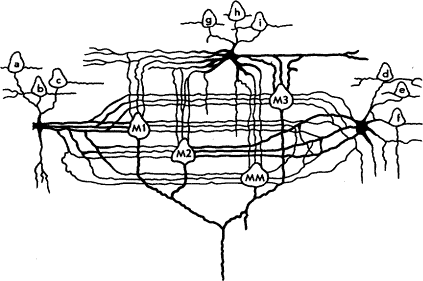
Такая новая организация по-прежнему должна обеспечивать взаимодействие между её тринадцатью управляющими, представленными здесь, как и ранее, в реальной жизненной ситуации. Но теперь сделано так, что подчинённые а, b, с могут поддерживать обмен информацией друг с другом и способны формулировать своё мнение. Однако теперь недопустима индивидуальная передача своего мнения руководителю M1 — при всякой передаче оно неизбежно будет отражать их общее мнение. Как мы видим, появились три линии связи между подчинёнными и их руководством. Это совпадает с архитектурой коры головного мозга, а также соответствует практике действующих предприятий. По любому серьёзному вопросу ни ответственный руководитель, ни его подчинённые теперь не будут ограничены одноразовым изучением вопроса, если, конечно, он сложный. В нашем примере предполагается, что здесь будут три попытки «разобраться в том, о чём доложить начальнику» — так будут понимать положение его подчинённые. Предприниматель же может воспринимать эту операцию как три попытки узнать, «какая чертовщина у них на уме». Во-вторых, из схемы на Рис. № 40 следует тот несомненный факт, что а, b, и с наряду с M1 могут общаться с любыми другими вышестоящими руководителями, хотя они им не подчинены. Более того, они могут так поступать, поскольку этого хотят другие руководители. Во всяком случае, при решении любого вопроса руководитель М1 может допустить одну крупную ошибку из двух, которые он делает на каждый десяток. Кроме того, все заинтересованные знают, что существует много способов прояснить проблему, а её обсуждение — процесс полезный. В действительности это не вопрос подсчёта голосов за и против. Таким образом, эта модель, основанная на нейроцитологии, позволяет каждому объяснению задачи M1, M2 и M3 не только быть повторённым каждому из начальников, но быть переданной также другим руководителями. Наконец, весьма важно спустить ММ (хотя он и ответственный за все) с его пьедестала на грешную землю. Он теперь не находится в изоляции, при изоляции же недолго ему быть самым ответственным. Если он будет относиться к своим непосредственным подчинённым с уважением, то есть как к коллегам, среди которых он первый среди равных, то будет вместе с ними участвовать в процессе выработки решений. Более того, он не станет выше того, чтобы не получать информацию со следующего за ними уровня иерархии. Руководители M1, M2, и M3 (в организации с жёсткой подчинённостью) могут энергично протестовать против прямого канала связи между их подчинёнными и ответственным руководителем, тем, кому они сами подчинены. Но в любой реальной ситуации, считающейся вполне здоровой, именно так и происходит, поскольку, возможно, ММ не до конца доверяет суждению M1 и, кроме того (мы в реальном мире), подчинённый a хотел бы, чтобы ММ его заметил лично. Со своей стороны ММ не хочет ограничивать свои живые источники информации только подчинённым M1. Кто они, те люди, которые советуют руководителю M1? Как они выглядят на самом деле? Насколько разбираются в деле (коль скоро этим определяется значимость совета M1)? И так далее. Таким образом мы находим в схеме Рис. № 40 оценку подобной мозгу организации, обеспечивающей процесс принятия решения на высшем уровне. Здесь, как и раньше, 13 управляющих, но на этот раз они выгладят разумно организованными. Теперь совершенно на тех же, что и раньше, условиях попытаемся рассчитать надёжность решения, которое ответственному руководителю предстоит передать выше. Считая, что все 13 человек могут ошибаться, может показаться, что все их ошибки будут теперь часто повторяться, так что результат станет хуже, чем раньше. Как мы увидим, этого не случится. По прежнему по каждой линии проходят три сообщения. Но они не независимы. Вероятность ошибочности каждого сообщения по-прежнему равна 0,3, тогда вероятность их ошибки составляет 0,33. Вероятность того, что a получит правильный совет от своих подчинённых, следовательно, составит (1 — 0,33) = 0,973. Однако теперь каждый вышестоящий управляющий получает ответ от каждого из трёх источников, что обеспечивает общую вероятность правильного ответа, определяемую произведением возведённой в куб вероятности, характеризующей безошибочность совета подчинённого на вероятность сделать правильное суждение ему самому. Мы уже установили, что M1, M2 и M3 способны принять правильное решение с вероятностью 0,8, в то время как их ответственный руководитель — с вероятностью 0,9. Предполагаемая нами модель учитывает мнение ответственного как коллеги трёх его заместителей, так что здесь уже четыре человека, рассматривающих проблему на равных как консорциум, в котором каждый в среднем может в отведённое ему время составить правильное суждение с вероятностью 0,825. Это означает, что любой из четырёх может правильно ответить с вероятностью: р = (1 — 0,33) (1 — 0,33) (1 — 0,33) 0,825 = 0,76. Однако поскольку все четверо обдумывали проблему вместе, суммарная вероятность совершить ошибку составляет: р = (1 — р)4 = 0,0033. Таким образом, вероятность того, что вся система в целом (см. Pис. 40) ошибается, оказывается равной 0,0033. Другими словами, вся группа руководителей (как целое) едва ли вообще сделает ошибку, по крайней мере пока они будут действительно сотрудничать. Вот так ловко работает мозг, и так же уже сегодня работает преуспевающая администрация. В этом и состоит способ получения надёжного результата из ненадёжных компонентов. Все мои попытки сводятся к тому, чтобы дать убедительные доказательства их взаимного успеха. Из этого явно следует, что мы обязаны всегда помнить о наличии лучшей организационной структуры предприятия, чем предоставляемая общепринятой схемой, и принять несколько допущений, которые,
Два этих вывода и до некоторой степени третий вытекают из нашего анализа. Более пространные доказательства третьему дают поведенческие науки, которые неоднократно экспериментальными измерениями чётко подтверждали справедливость такого вывода. На нашей схеме показаны только горизонтальные линии связей (поскольку и без того картина оказалась сложной). Здесь возникает следующий вопрос: каким образом управлять системой такого типа? Всякий читатель, быстро разобравшийся в том, что в реальной жизни группы людей действуют скорее так, как показано на Рис. № 40, а не на Рис. № 39, сочтёт, что я старался открыть Средиземное море». Конечно, так люди и действуют», — скажет он. Работа подобной системы обычно называется «политической». И успех приходит только к проницательному, опытному руководителю вследствие чрезвычайной сложности путей связи между людьми. Более того, самое характерное в мультиноде — это политика, то есть явно выраженная возможность манипулировать другими людьми в своих собственных целях, изменять своему начальнику, сотрудникам или коллегам. Однако должен существовать и лучший ответ, чем этот. Причина, по которой не требуется лучшего ответа, кроется в том, что мультинод, как мы знаем, может действительно работать, но, чтобы он успешно сработал, требуется очень много времени. Методы его работы развивались в более неспешные века. В первой части мы исследовали причины, вследствие которых в условиях стремительного развития технологии потребовались более быстродействующие средства адаптации. Между тем мультинод часто вовлекает значительно большее число людей, чем то, которым мы до сих пор оперировали; более того, людей не стоящих неподвижно на четких иерархически установленных позициях по отношению друг к другу. Мультинод может включать коллег из других стран, авторитет которых соответствует их положению, но едва известен в данной стране, и даже псевдоколлег (таких, как руководители отделов и управлений правительственного аппарата, с мнением которых считаются в промышленности), но которые не занимают официального положения в данной организации. Далее, существуют советники и различные специалисты (которые могут, например, работать в консультативных фирмах или университетах), мнение которых весьма важно при принятии данного решения, но они также не занимают никакого официального положения в фирменной иерархии. Все это делает реальные проблемы реальных мультинодов значительно более трудными, чем те, с которыми пришлось столкнуться при рассмотрении выдуманной нами схемы на Рис. № 39. К счастью, однако, предложенная нейрокибернетическая модель по-прежнему лучше других соответствует более сложным реальностям современного мира. Мы утверждаем, что знаем, как всё работает. Проблема в том, как сделать, чтобы работа шла быстрее. Это, конечно, должно означать введение в том или ином виде дисциплины и порядка. Это, однако, означает также, что не могут быть одновременно введены какие-либо меры для обеспечения в трудные времена завидной свободы и удивительной гибкости действий мультинода. Если бы люди могли понять, как этого достичь, не одевая на себя и свою организацию смирительную рубашку, то сохранился бы некоторый шанс реализации такого нововведения, как мультинод. Один метод — метод жёсткого порядка, хотя и относится к числу чаще всего практически используемых, поскольку никто не хочет подумать о других, должен быть исключён, с чем следовало бы теперь согласиться. Только что отвергнутый нами искусственный пример ясно показал, почему такой подход к проблеме непригоден. Говоря точнее, он искажает естественные свойства системы со всеми её внутренними возможностями давать правильное решение. Тогда попробуем подойти к проблеме научно, используя Всё, чему учит кибернетика, и, в частности, сохраняя характерную для мультинода избыточность и гибкость, которые делают его столь мощным инструментом выработки правильных ответов. Ниже следует такой кибернетический план. Первая трудность в том, чтобы установить, какого типа проблемы мультинод действительно решает. Ни сам он, ни установленное им старшинство, ни власть не предназначены для определения тривиальных результатов — он не обязан этим заниматься. Более всего он нужен для выработки весьма ответственных планов (стратегических) и, следовательно, решения весьма сложных проблем. Дело в том, что люди представляют себе обдумывание как процесс синтезирования общего, но всестороннего заключения, основанного на большом числе компонентов. Решение видится как красивое нагромождение одного юридического условия на другое. Вот почему, вероятно, всякий, кто пытается провести «согласованное» решение, сталкивается с бесконечной проблемой переписывания проекта такого документа. В кибернетике подход иной. Результат процесса обдумывания — решение — принимает следующую форму: делать только так (а не как-нибудь иначе). Как только начинается процесс обдумывания, мультинод сталкивается не с определённым числом строительных блоков, а с кажущейся бесконечностью возможных решений, из которых нужно сделать выбор. Именно изобилие возможностей «кричит» и требует решения прежде всего. Затем, в соответствии с нашей моделью, процесс, которому мы стараемся содействовать, сведётся к «отсечению» двухсмысленностей и неопределённостей, продолжающемуся до тех пор, когда можно будет сказать: «делать только так». Короче говоря, мы хотим измерять разнообразие комплексных решений с самого начала, измерять уменьшение разнообразия, вызванное каждым заключением, к которому мы приходим к процессе обдумывания, и в общем руководить всеми операциями мультинода до тех пор, пока разнообразие не сведётся к единственному — самому решению. Чтобы сделать это, нам потребуется два инструмента: парадигма логического поиска и средства измерения — правило и мера — для измерения неуверенности. Парадигма логического поискаПарадигма — это образец; в нашем случае — образец фундаментального подхода к решению определённой общей проблемы, который может быть полезен для множества различных ситуаций. Конечно, существует много путей проведения поиска, но в случае поиска решения люди обычно приближаются к нему последовательно. «Что, — спрашивают они, — прежде всего надо решить? Что решать после этого?» Следует отметить, что инструмент, разработанный к настоящему времени наукой управления в помощь подготовке комплексных решений, полагается на последовательность логических приоритетов. Парадигмой этого метода поиска является дерево решений. (Предпринять это в США, Великобритании или Франции? Ответ: Во Франции. Предпринять это в Париже, Лионе или Марселе? Ответ: В Париже. И так далее.) Созданное нами понимание возможности мультинода свидетельствует, что такая парадигма — не то, чего мы хотим. Конечно, помощники-учёные могут попытаться логически определить первостепенные задачи и пытаться также склонить мультинод рассматривать их первыми. Обычно он этого не делает, не может или не станет делать. У мультинода свои методы. Кроме того, кто скажет, что на самом деле приоритетно? Подобное решение само по себе относится к числу тех, которые мы назвали «политическими». Нет, мы должны придерживаться нашего понимания мультинода — его избыточности, гибкости и свободы. Наша поисковая парадигма должна быть свободна от приоритетов. Иначе мы станем диктовать мультиноду, как ему работать совершенно не подходящим образом. Простой пример процедуры поиска возникает при отыскании определённого пункта на карте. Карты разделены на квадраты, и можно считать, что масштаб и сетка взаимосвязаны так, что если мы попадем в нужный квадрат, то там и найдём нужный пункт. Рассмотрим тогда карту, разделённую на части через равные расстояния по обеим осям так, чтобы получилось по 1000 квадратов в каждом направлении. Это должно означать, что на карте теперь сетка с 1 000 000 квадратов. В нашем распоряжении две парадигмы для осуществления поиска. Ясно, что по окончании этой длительной процедуры мы можем сказать: «Разыскиваемый нами пункт находится в квадрате номер 342756». Такой метод действительно срабатывает как подчиняющийся закону необходимого разнообразия. Мы определили нашу задачу в виде множества 1 000 000 и теперь предложили рассмотреть поиск в миллионном множестве. Но, как каждый школьник знает, есть парадигма, лучшая, чем эта. Он предложит пронумеровать квадраты по горизонтальной и вертикальной осям и определять каждый квадрат с помощью таких координат. Эта вторая парадигма точно определяет генератор разнообразия. Поскольку можно записать 1000 + 1000 = 2000, мы в состоянии получить их произведение 1 000 000 — как общее разнообразие. Проблема размещения пункта и его поиска теперь уменьшена с разнообразия 1 000 000 до разнообразия 2000. Так произошло, поскольку мы прибегли к двумерному логическому пространству. Что касается самого поиска, мы не знаем, сколько квадратов сетки нам придётся проверить, прежде чем найдём нужный. При первой парадигме с разнообразием 1 000 000 можно попасть в цель как в самом первом квадрате, так, с другой стороны, и в самом последнем. Тогда мы заявляем, что в общем средняя длина поиска составляет половину миллиона квадратов. При второй парадигме мы вначале определяем номер квадрата по горизонтали, а затем по вертикали; этот процесс в среднем потребует 500 + 500 операций проверки, а всего 1000. Говоря математически, первый способ поиска требует числа шагов, эквивалентного половине общего множества (500 000), в то время как второй путь требует числа шагов, равного половине двух корней квадратных из общего множества: 2 (V)^½/2 = V½. Вторая парадигма очень мощная, поскольку является генератором разнообразия. Именно такой подход мы будем использовать. В аналогичных проблемах, перед которыми мы стоим, мы не имеем дела с двумерной картой. Мы имеем дело с задачами, сформулированными в многомерном логическом пространстве. Иначе говоря, размерность решения не просто «север-юг, восток-запад», здесь столько логических вариантов, сколько их может быть в самой проблеме. Любое серьёзное решение в промышленности обычно увязывается с такими вещами, как производство, сбыт, финансы, персонал, научно-исследовательские и опытно-конструкторские работы… Именно они определяют размерность проблемы, поскольку решение, по определению, является условием существования. Тогда можно сказать, что в общем размерность любой проблемы, достойной мультинода, есть n– размерность (и можно заметить наперёд, что n не менее 5 и не более чем, скажем, 20). Для n > 1 вторая парадигма оказывается более мощной, чем нам представлялось до сих пор. Вспомним, что общее разнообразие определяется перемножением множества разнообразий. Так, в случае карты, разнообразие по каждому из двух измерений составляло 1000, что дало в результате общее множество 1 000 000. Если бы оно распространилось на трёхмерную структуру, то общее множество составило бы тогда 1 000 000 000. В общем, для случаев принятия решения суммарное разнообразие равно произведению разнообразия по одному типичному размеру на число других размеров а средняя длина поиска в соответствии с первой парадигмой составляет половину этого числа. Оно обязано быть гигантским. В случае избранной нами парадигмы, однако, средний поиск составит половину числа разнообразия, умноженного на корень n-й степени из общего разнообразия. Все это простое обобщение примера с «картой» для n-мерного пространства. Записанная математически длина поиска будет равна: (n/2) V1/n. Сделанный нами вывод в высшей мере важен. Прежде всего расчёт подсказывает, что в случае карты, которая, как известно, двумерна, для достижения цели вместо половины миллиона шагов (первая парадигма) потребуется в среднем всего тысяча шагов (вторая парадигма). Это представляет колоссальное увеличение эффективности подготовки решения, поскольку предпринимаемые нами усилия теперь составляют одну пятую процента по сравнению с первым методом. Когда число измерений, учитываемых при решении проблемы, возрастает с двух до n, возрастание эффективности становится астрономическим. Следовательно, в модели, создаваемой для подготовки сложного решения, должны быть прежде всего учтены логические измерения, а также обозначены пути взаимной связи между ними. Модель не должна точно указывать последовательность решений, которая будет установлена самим мультинодом, Мера неопределённостиСама идея о необходимости измерять неопределённость, связанную с решением, должна казаться большинству людей обескураживающей. Фактически, однако, наука уже создала соответствующую меру, весьма полезную во многих областях научных исследований. Она называется «энтропией». К несчастью, само понятие энтропии многих пугает, и поэтому я не стану его раскрывать здесь. Использование этого понятия в интересах управления тщательно разъяснено и продемонстрировано в моей книге «Decision and Control» («Решение и управление»), к которой я отсылаю всякого, кто хочет детально и глубоко в этом разобраться. Для целей настоящей главы вполне достаточно определить эту меру как очень полезный инструмент, не переходя к сложным математическим или физическим обоснованиям. (Обо всём этом, однако, пришлось упомянуть, чтобы подготовленный читатель не обвинил меня в изобретении колеса). Неопределённость, как мы видели, является функцией разнообразия. Разнообразие есть численная мера возможных состояний системы. Решение есть результат выбора одного возможного состояния из всех других. Теперь вернёмся к примеру с картой. Из миллиона квадратов (на географической сетке) нам нужно выбрать один. Очевидно, что мера неопределённости, связанная с подобным «решением», начинается с миллиона и снижается до единицы. Теперь рассмотрим управленческое решение, но будем придерживаться скромной размерности задачи. Пусть у нас будет восемь изделий и восемь станков. Каждое изделие может быть изготовлено на любом станке. Тогда «решение» можно представить как определение того, какое из восьми изделий и на каком станке должно производиться в настоящее время. Это будет двумерная задача с разнообразием, равным восьми по каждому измерению. Нетрудно видеть, что из 64 вариантов нам предстоит выбрать один. Таким образом наша проблема сводится к снижению разнообразия с 64 до 1. Далее, можно ввести ещё одно измерение. Предположим, что каждое изделие выпускается в восьми вариантах — красное, голубое, зелёное и так далее. Тогда решение, которое мы пытаемся принять, становится задачей выбора одного ответа из 8 × 8 × 8 = 512 вариантов. Если бы число изделий было намного больше и намного больше была бы размерность проблемы, то число вариантов такого разнообразия стало бы астрономическим. Заметьте причину этого явления — все их численные показатели должны перемножаться. Каждого прошедшего школьный курс математики это обстоятельство сразу же наводит на мысль о возможности использования логарифмов. Если бы мы использовали логарифм разнообразия по каждому измерению, то для определения общего разнообразия — там пришлось бы просто суммировать эти цифры. Но здесь возникает небольшое препятствие: большинство читателей имело дело с логарифмами по основанию 10. В кибернетике используются логарифмы, вычисляемые по основанию 2. Это обусловлено тем, что исходным положением для решения является выбор между «да» и «нет». Такое бинарное различие (вспомните первую часть) называется битом. Более того, четыре, вещи мы можем различать с помощью двух битов информации. Мать и отец, их сын и дочь могут быть по-разному определены: «решением», во-первых, кто из них мужчина и кто женщина, и, во-вторых, кто первого и второго поколения. Нам необходимы три бинарных решения, чтобы различить восемь состояний, четыре бита нужны для различения 16 состояний, пять битов — для различения 32 состояний и так далее. Это всё, что имеется в виду под фразой «вычисление логарифма по основанию 2». При десяти бинарных решениях можно различить 1024 состояния. И если все это ещё не звучит достаточно впечатляюще, то следует добавить, что эти величины растут экспоненциально. Сорок бит позволят распознать одну особь в популяции, превышающей примерно триллион (1012.) Всё, что мы теперь делали, сводится к созданию полезного арифметического метода, позволяющего рассчитывать неопределённость. Восемь вариантов, восемь изделий, изготавливаемых на восьми станках, создают 512 вариантов. Такова мера нерешённых проблем, пока не достигнуто заключение относительно того, какой вариант, какого изделия, на каком станке будет выпускаться. Теперь давайте используем наш логарифмический метод. Разнообразие из восьми вариантов по каждому измерению может быть заменено числом бит (а именно логарифмом по основанию 2), требуемых для его выражения. Для такого разнообразия ответом будет три бита (здесь 3 бита: 8/2 = 4; 4/2 = 2; 2/2 = 1). Общее разнообразие, вместо 8 × 8 × 8 = 512 вариантов теперь составит 3 + 3 + 3 = 9 бит. Нет нужды говорить, что оба этих разнообразия эквивалентны, поскольку 9 бит равны 29 = 512. Смысл предложенного здесь метода в том, что мы можем создать модель предстоящего решения, основанную не на последовательности приоритетов, и что будем измерять общее разнообразие решений. Тогда любое заключение, полученное мультинодом, будет сокращать разнообразие как общую неопределённость. Более того, исключённое разнообразие будет не просто разнообразием, относящимся к вариантам, непосредственно снятым с рассмотрения, но также к исключённым из разнообразия, относящегося к другим измерениям данной проблемы, теперь признанным и не имеющим к ней отношения как следствия ранее принятого нами решения. Вспомним, что мы разыскивали город, который не только находится на определённой широте, но он и не может находиться в море, а это ограничивает поиск его широты. Когда мультинод начинает принимать решения, что делается отсечением разнообразия в определённом логическом измерении, он неявно ускоряет уменьшение разнообразия. Возвратимся к примеру вариантов восьми изделий, выпускаемых на восьми станках, и предположим, что мы сняли четыре станка. Разнообразие тогда составит 8 × 8 × 4 = 256. Иначе, начав привыкать к нашей новой идее, предпочтительнее записать, что первоначальное разнообразие 3 + 3 + 3 = 9 битов теперь уменьшилось до 3 + 3 + 2 = 8 битов (= 256). Здесь мы подошли к важному моменту. Мы считаем, что уменьшили разнообразие на один бит. В действительности На этом примере мы, таким образом, пытаемся изучить действенность нашей второй парадигмы при n-мерной проблеме (хотя в данном случае n <3). Механизмы, с помощью которых реализуется его «сила парадигмы», сводятся к объединению логических переменных и размещению этих переменных в разных измерениях. Тогда, хотя мультинод может не рассматривать последовательно свои решения в приемлемом порядке их приоритетов, любое принятое им решение будет, вероятно, отражаться во всей системе и, следовательно, усекать разнообразие с огромной скоростью. Здесь уместно сделать два замечания. Первое состоит в том, что кажущаяся ошеломляющей, неопределённость при принятии любого решения в реальной жизни с самого начала быстро уменьшается до тех пор, пока не останется очень мало вариантов выбора решений. Действительно, можно доказать математически, что разнообразие по мере принятия промежуточных решений уменьшается экспоненциально. Второе замечание более интересно с точки зрения психологии управляющих. Отнюдь не ясно (судя по нашим наблюдениям), что управляющие, принадлежащие мультиноду, понимают силу влияния, которое оказывает кажущееся маловажным их промежуточное решение. Следовательно, они недооценивают важность достижения логической последовательности нахождения решений. Вероятно, главный выигрыш, достигаемый описанной здесь процедурой при подготовке реальных решений, состоит в том, что при неограниченной свободе действия мультинод может показать (даже в количественном выражении) влияние того, что с первого взгляда кажется второстепенным, на общую структуру окончательного решения. Парадигма поиска и мера энтропии — вот всё необходимое, что позволяет мультиноду помочь научному решению рассматриваемых проблем. Но, как свидетельствует опыт, люди нелегко понимают подробности работы такого метода на практике. По этой причине мы завершим этот раздел примером. Было бы полезным привести реальный пример использования этого метода на практике (поскольку он показал своё «могущество»), но, к несчастью, это невозможно — реальные примеры слишком сложны. Во-первых, они требуют больше исходной информации для понимания происходящего, чем можно привести в книге, и больше алгебраических расчетов, чем допустимо для иллюстрации. Во-вторых, реальные примеры — фирменный секрет. Нет смысла использовать наш метод, если проблема на самом деле недостаточно серьёзна, но по реальному примеру можно установить фирму — его источник. Более того, сила этого метода именно в том, что он потенциально может показать слабости любого управляющего, которые могут при этом выясниться. Так происходит потому, что принятие мультинодом неверного решения или принятие решения в логически неверной последовательности очень наглядно проявляется. Постепенно уменьшающееся, как было сказано, по экспоненте разнообразие внезапно (в каждом взятом из реальной жизни примере) возрастает по ходу рассмотрения проблемы мультинодом. Этого не должно быть. Конечно, так случается в результате аннулирования ранее принятых неверно решений или вследствие переформулирования проблемы. В обоих случаях факт использования этого метода оказал огромную помощь заинтересованному руководству, но пересказ всех обстоятельств в реальном примере поставил бы их в глупое положение перед публикой. Эта глава, следовательно, будет закончена придуманным примером использования мультинода. ПримерРассмотрим введение в производство нового товара. Факторы, которые нам придётся учитывать, не исчерпывающие, но они типичны для факторов, которые должно учитывать руководство. При определении этих факторов мы окажемся перед необходимостью обозначить шесть измерений логического пространства подготовки решения. Далее, число вариантов по каждой логической переменной выбирается произвольно, но, подчёркиваю, они весьма правдоподобны. Задача состоит в том (как было сказано), чтобы принять решение о новом товаре, но мультинод тотчас же признает, но дело здесь значительно сложнее, «поскольку хотят сотворить чудо». Решение о производстве нового товара означает точное определение всех особенностей его характеристик, включая замысел его разработки, производства и сбыта. Поэтому паше решение превращается в нечто такое, что требует тщательной проработки. Но мы будем придерживаться мнения, что это решение на самом деле станет достаточно простым, если упростить его и снизить исходную неопределённость до такой степени, чтобы сказать: делать так. Теперь рассмотрим весь процесс, предлагая правдоподобные переменные, и оценим правдоподобные изменения каждой из них. 
Перечислив соответствующие логические переменные и измерив из разнообразие, мы обнаружили, что общая неопределённость, которую предстоит разрешить, составляет 17 бит. Это означает, что нам предстоит принять по крайней мере 17 бинарных решений для того, чтобы уменьшить число возможных вариантов с 131’072 до одного единственного. Это и есть тот многократный и последовательно осуществляемый процесс принятия решений, которым мы пытаемся управлять. Алгебра решенийСледующий шаг состоит в том, чтобы определить, влияние одних переменных и» другие. Любое решение относительно заводской стратегии влияет на планы движении денег и, конечно, на кадровую политику (может быть, нам придётся закрыть завод, цех); оно скажется на маршрутах разработки (некоторые из приборов нельзя сейчас купить). Однако мы можем решить, что производственные изменения на заводе не скажутся ни на стратегии, ни на планах сбыта, поскольку мы можем, например, но мере изготовления накапливать изделия на складах. Затем мы должны рассмотреть влияние любого решения в отношении переменной Р на F, S и R. По окончании такого анализа относительно каждой логической переменной мы сможем составить полный перечень логических зависимостей, где значком * будем отмечать, что «любое решение о предшествующем влияет на последующие». Всё это может выглядеть следующим образом: Оператор основных зависимостей
Следует заметить, что логические зависимости не обязательно рефлсксивны. В нашем примере любое решение в отношении кадровой политики может отразиться на финансовых потоках, так как, возможно, придётся платить лишнее, но примем, по решения относительно финансирован! i не влияют на кадровую политику. (Конечно, может быть и наоборот — наш пример придуман и упрощён.) Следующий шаг состоит в извлечении из оператора (А) предварительной логической группировки переменных. Во всяком случае, либо Р, либо М влияет на F, R и S. Если мы по случайному стечению обстоятельств являемся знатоками применения логической алгебры и её методов, то должны начать здесь записывать формальные предположения, как того требует символическая логика. Однако в этом нет необходимости, поскольку следующая таблица, вытекающая прямо из оператора (А), помогает решить задачу. Оператор базовых зависимостей (В):
Чтобы получить из известных в этой системе решений логические группы, нам следует начать записывать высказывания, объединяющие наши переменные, начиная с визуального изучения таблицы (В). Преобразованный оператор логических групп
Теперь удостоверьтесь, что все зависимости из оператора (А) вошли в оператор (С). Заметьте также, что мы уже перестали думать о смысловом содержании буквенных символов. В этом сила манипуляционной алгебры — она облегчает размышления и делает их более строгими. Конечная цель всех наших процедур — получить возможность записать систему решений в едином высказывании, охватывающем все логические зависимости. В этом будет состоять следующий этап группирования как процесс объединения шести высказываний, вышедших в оператор (С). Сделаем первый шаг в этом направлении. Вызывает недоумение высказывание (6) — в нём только две переменные. Нам следует от него избавиться, введя зависимость от D в С всюду, где она присутствует. Для этого нужно ввести новый символ — обычную точку, имеющую смысл «и». Рассмотрение Р или М в высказывании (I) требует рассмотрения F и С и Р; мы уже знаем, что рассмотрение S распространяется и на рассмотрение D, но это неверно в отношении F и R. Переписав (I) и < 6) совместно, получим PM * (FR. S * D). Такой оператор требует весьма тщательного изучения, поскольку здесь к понятию группы добавляется понятие гнезда. Пары РМ и FR — группы, но выражение, заключённое в скобки, представляет собой логическое гнездо, так как всё оно предопределяется группой РМ. Следует отметить, что при отсутствии скобок данное высказывание может восприниматься как PM * FR и S * D. Это было бы неточным гнездом. Оно верно но не адекватно. Теперь, проделав то же самое с высказываниями (3) и (5), запишем пять высказываний (преобразованные помечены буквой а). Оператор первого гнездования (D)
То, что произошло теперь с утверждением (5), весьма интересно. Прямая подстановка даёт (S * DD) * PF. Как дополнительный символ D, так и скобки излишни. Тогда (5a) можно прочесть как (S * D) * PF или S * (D * PF) — оба утверждения верны. Теперь сразу видно, что высказывание (5a) можно исключить, поскольку оно приняло знакомую нам форму: PF предопределяется высказыванием S * D, которое уже встречалось дважды. Оператор второго гнездования (Е)
Проверка оператора (Е) подсказывает, что (1b) и (3b) можно объединить, поскольку их правые части почти эквивалентны. Чтобы сделать их такими, следует вынести R из (1b) и Р из (3b) и записать эти две переменные в левой части импликации: [(PM* R) (RD* P)] (F. S* D* PF). Сделав такой шаг, мы произвели перегруппировку и перегнездование. Мы поступили так, поскольку нет единственного способа формулирования сложных логических проблем, во всяком случае не более, чем для множества уравнений в математике. В алгебре есть способы манипулирования, а критерием успеха является соответствие результата. Разность а^2 — b^2 может быть подходящим способом выражения разности площадей двух квадратов, тогда как произведение (а + b) (a — b) может стать более подходящим для другого случая. Но оба выражения «верны». Все пока сделано хорошо, поскольку мы избавились от половины первоначальных высказываний. У нас осталось одно полное высказывание, показывающее зависимости в групповой и гнездовой форме, и два первичных высказывания из оператора (С), а именно: (2) и (4). Теперь обратим внимание на них: FR*PM (2) Поскольку общим в обеих зависимостях является наличие F в первой группе, было бы, вероятно, желательно записать их в виде F * PMRD (сопоставьте с оператором (А): F*PD (M*RD) (R*PM), (2 а) А затем переписать как: F* [PD. M* (DP*PM)]. (2b) Это выражение можно ввести в правую часть выражения (1с), но мы не можем пренебрегать высказываниями (2) и (4), то есть M * RD и R * PM, поскольку они ранее фигурировали в левой части выражения (1с). Из множества путей их объединения наиболее удобным кажется следующий: переписать (PM * R) как (PM * R) (M * D), поскольку M * PD, и (RD * P) как R * PM) (D * P), поскольку R * PM. Тогда левая часть выражения (1с) сведётся к выражению [(PM*RPM) (M*D*P)]. Продолжая тем же способом, получаем: Окончательный оператор (F):[(PM*R*PM) (M*D*P)] * [F* [PD. M*(D. R*PM)] S*D*Pf]. В окончательном операторе символ F выделен курсивом. Это утверждение используется, чтобы показать, что полное перечисление его последствий здесь опущено. Логика, конечно, приведёт вновь к операторам, предшествующим F. Ранее отмечалось наличие многих логически эквивалентных путей написания этого полного выражения. Что мы выиграли от того, что записали одно из них в столь сложной форме? Вопрос вполне правомерен, поскольку общее выражение можно было бы (на языке логики) сильно сжать. Ответ в том, что мы стремились к пониманию системы логических решений и к предоставлению возможности самостоятельно рассмотреть множество подходов к решению, поскольку мультинод может выбирать любой путь, который ему предпочтителен. Предположим, что уже почти принято решение, касающееся планов сбыта. Один из восьми рассмотренных при этом планов начинает выглядеть непривлекательным и исключается. Тогда мы обращаемся к оператору (F) слева и смотрим на D. Согласно первому правилу мы должны рассмотреть влияние этого решения на Р. Дальше мы замечаем, что это же решение влияет на F, и далее рассмотрение должно распространиться на М (фактор Р уже был рассмотрен, а D оказался избыточным). Рассмотрение М включает его влияние на фактор R, в свою очередь влияющий как на Р, так и на М. Далее, F означает также обдумывание в отношении фактора S, который прямо влияет на D, о котором и идёт речь, а последний влияет на Р и F, о чём мы уже знаем Такова будет интерпретация системы, если она начинается с D. Попытайтесь теперь сформулировать разумные правила для проверки влияния решения относительно D исходя из первой таблицы — оператора (А). Новое обращение к переменным быстро приведёт Вас к неразрешимым узлам противоречий. Попытайтесь изобразить все это графически — график быстро станет выглядеть как запутанный котенком клубок ниток. Мы снова оказываемся в плену растущего многообразия. Итак алгебра решений дала нам уже полезное руководство, но наша действительная цель состояла в том, чтобы создать полезную метрику-измеритель решения. Тогда для этой цели мы обязаны записать наш оператор (F) полностью, иначе говоря, мы обязаны показать варианты. Фактор Р имеет четыре составляющие возможные заводские стратегии. Тогда там, где в операторе (F) присутствует Р. следует писать: Р (р1, р2, р3, p 4) и так далее. Давайте теперь вернёмся к рассмотрению D или, как мы условились, представим его в виде D (d 1, d 2, d 3, d 4, d 5, d 6, d 7, d 8). В соответствии с нашим примером один из этих планов отпал — таково было решение. Первое заключение тогда состоит в том, что разнообразие D уменьшено с 8 до 7, то есть с 3 до 2,8 бит. Это означает, что общая неопределённость уменьшилась на 0,2 бита. Назовём её явным показателем принятого решения. Однако мы знаем, что осталось ещё много более важных факторов, чем этот и у нас есть правило выяснения дальнейших эффектов. Что можно, например, сказать относительно четырёх стратегий производства? Планы 2 и 4, как мы выяснили, неэффективны, хотя мы давно заявили, что стратегия производства не влияет на планы сбыта (поскольку изделия могут храниться на складах), но обратное неверно Давайте примем, что возможность dg, теперь исключённая, была единственным планом распространения нашего товара в отдалённых уголках страны. Продажа именно в этих районах придавала смысл производственным стратегиям-планам 2 и 4, поскольку в них предусматривалось использование расположенных там предприятий. Если бы эти производственные стратегии были сначала исключены, то план dg, однако, мог бы быть реализован с помощью почтовых пересылок. Всё это означает, что в процессе уменьшения общей неопределённости в 17 бит всего на всего на 0,2 бит, то есть при исключении варианта dg, первоначальная неопределённость для Р уменьшается на 1 бит. Но мы показали, что все это сказывается и на F. И в самом деле, планы движения денег f и f — L и f, связаны (как выяснилось) с реализацией стратегий производства 2 и 4. Разнообразие вариантов для F снизилось при этом с 8 (3 бита) до 4 (2 бита) — ещё одно уменьшение неопределённости на 1 бит. Логика заставляет нас рассмотреть влияние всего этого на переменную М. Теперь если нельзя рассчитывать на распространение нашего товара в отдалённых регионах (d8), то это, без сомнения, означает изменение стратегии сбыта. Конечно, следовало бы об этом подумать сразу. Если так, то как же следовало бы воспринимать решение об исключении d 8 до обсуждения рассмотрения стратегии М? Кто принял это решение, да и было ли оно правильным? Это именно те вопросы, которые наш метод управления побуждает нас ставить, ставить быстро и без обиняков. Допустим такую возможность, что в конце концов полностью возобладает решение d 8. Toгдa большинство рыночных стратегий, в которых столько внимания отводилось проблеме торговли в отдалённых регионах, может стать неуместным. Предположим что пять из них исключаются. Тогда останется три, то есть неопределённость составит всего 1,58 бита. Это говорит о том, что пришло время рассмотреть R. Для этой переменной, как ни странно, ничего не изменилось. Рассмотрение нашего сценария как выяснилось, никак не влияет на характер нашего товара. В таком случае влияние R на Р и М не вызывает других последствий. Однако маршрут (D * P) * F * S по-прежнему требует рассмотрения. Здесь S, и S — как две кадровые стратегии, зависящие от этой цепочки, теперь отпадают как ненужные (легко догадаться, почему). Тогда неопределённость уменьшается ещё на 1 бит. Но это влияет на D. На первый взгляд цикл полностью завершён. Конечно, мы начали с рассмотрения D. Это верно, но мы, в частности, начали с исключения d 8. А что будет с d 2, d 4 и d 7 Оказалось (и это весьма правдоподобно), что последовательное исключение пяти стратегий сбыта и двух видов кадровой политики (как следствия отказа от do), действуя на и, приводит к исключению и этих планов сбыта. Последнее, как мы знаем логически воздействует на Р и F. К счастью, в данном примере (заметим для самооправдания) на производственных стратегиях данное воздействие далее не сказывается — хотя, упаси боже, в принципе могло бы сказаться. Но на Р действительно сказывается последовательное сокращение разнообразия F было вначале вызвано отказом от двух производственных стратегий. Теперь же, когда отпали ещё три стратегии сбыта потерял смысл и план f 5, как обслуживающий их нужды. Теперь обратимся к последнему оператору F, ставшему весьма важной составляющей. Нам вновь предстоит просмотреть все аргументы, начиная с первого появления F, поскольку число разнообразий этих планов теперь снизилось до трёх (1,58 бит). Кто-то сказал, что d 8 исключается, и с этим все согласились. Неопределённость принятия решения всей цепи решений претерпела уменьшение вследствие незначительного уменьшения её вначале на 0,2 бита. Теперь вновь рассмотрим все «поле боя» и определим реальную эффективность этого решения:
Так выглядит последовательность результатов, вызванных самым первым решением — исключить d8: 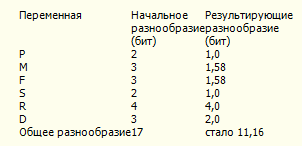
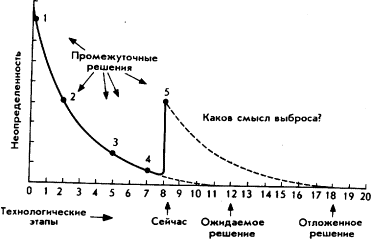
Итак, небольшое решение, всего на 0,2 бита уменьшающее неопределённость, фактически снизило её одним «ударом» на 5,84 бита. Число возможных вариантов таким образом сократилось с 130 000 до немногим более 2000. Такова сила мультинода и его многомерной программы. Такой мощью мультинод располагает сам, но он её не очень-то осознает. По этой причине ему необходимо руководство, методика работы. Мы пытаемся здесь объяснить эффективность группового решения (а не изобразить ее), а также дать средство для подкрепления и расширения значимости получаемых результатов (не узурпируя их). Можно было бы долго комментировать мой опыт работы этим методом, но я ограничусь подкреплением ранее приведённых объяснении того, в силу каких альтернативных причин энтропия селекции может на деле возрасти по ходу длительного процесса принятия решений. Предположим, что жирные точки на Рис. № 41 соответствуют промежуточным решениям, принятым в указанное на графике время (уменьшение неопределённости рассчитывалось по нашей методике). Тогда, строго говоря, нам следовало бы, представить этот график как гистограмму, в которой неопределённость падала бы в момент принятия промежуточного решения. Вместо этого здесь приведена гладкая кривая, поскольку она нагляднее демонстрирует ход событий, и, кроме того, частичным оправданием служит то, что мультинод стремится свести решения к единственному. Как видно, все шло хорошо до промежуточного решения 4, принятого в момент времени 7. Но к моменту времени 8 неопределённость, ранее сильно уменьшенная, внезапно возросла (возврат в систему принятия решении). Всякий, кто работал по этой методике, конечно, знает, что случилось. Он регистрировал и измерял неопределённость и отлично знает, какие ограничения были сняты. Однако, как это ни странно, оказалось далеко не просто понять, почему так произошло. Перед принимающим решение была альтернатива:
Почему некоторым не удаётся дать этому правильную интерпретацию? Если решение было умышленно, сознательно не реализовано («мы ошиблись») или если проблема была формально изменена («выступили совершенно новые факторы»), все ясно. Однако в реальной жизни мультинод, охватывающий многих людей, может быть далеко не уверен в том, что случилось. Все согласятся с тем, что если была общая договорённость в отношении промежуточных решений 2–4, то не было договорённости обо всех последующих. Если наша методика может успешно показать, что действительно произошло, то она, без сомнения, сослужила хорошую службу (хотя сама по себе требует «рекламы», поскольку мотивировки действия мультинода сложны и противоречивы). Но будем всё же прагматиками. Что важно для ситуации к моменту времени 8? Это просто то обстоятельство, что конечное решение («делать так»), которое, как мы в тайне надеялись, будет принято к моменту времени 12, оказалось достижимым значительно позже. В этой точке лидер мультинода, ответственный руководитель, должен усиленно добиваться того, что кажется приемлемым, или должен согласится на неизбежную задержку решения, или может подразделить проблему. Третий вариант наиболее интересен на практике. Оказывается, большинство бесконечных откладывании со дня на день принятия важных решений происходит не столько от «изменений» проблемы, сколько от степени её «прояснения (оптимизм) или «затуманивая» (пессимизм), вследствие чего неопределённость стремительно возрастает.
К несчастью, перед ответственным руководителем открыт и четвёртый путь. Ничего не предпринимать. Принятие решения может тогда затягиваться до бесконечности: при этом всякий раз, когда мы приближаемся к ответу в один бит — «делать так», неопределённость вновь резко возрастает. У меня есть график с шестью выбросами, последний из них отражает ту же неопределённость (после семи лет работы), что и самый первый. Это означает, что сложившийся в данном случае мультинод не мог подняться до сложности проблемы, перед которой он был поставлен. |
|||||||
Оглавление |
|||||||
|---|---|---|---|---|---|---|---|
|
|||||||