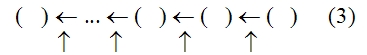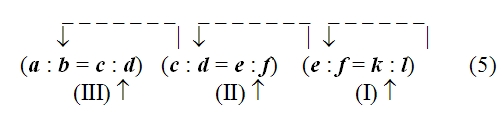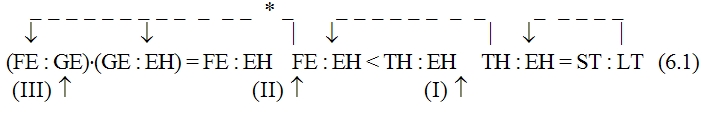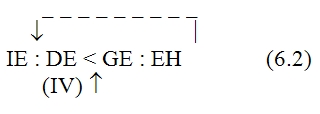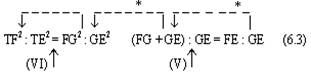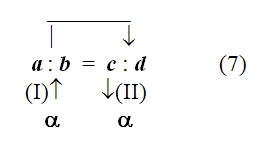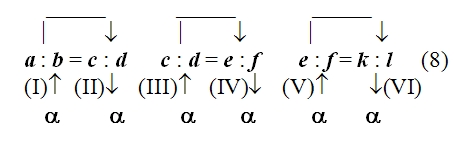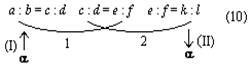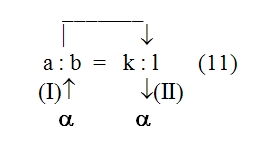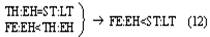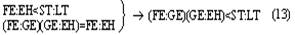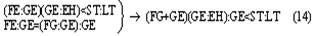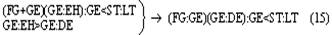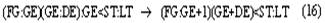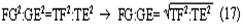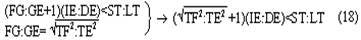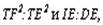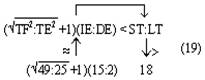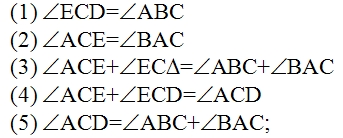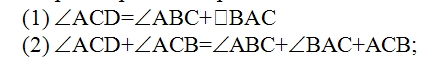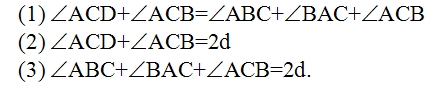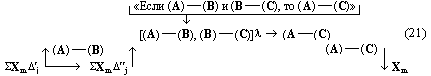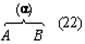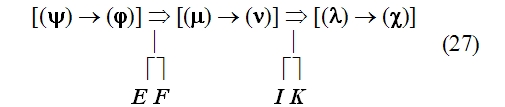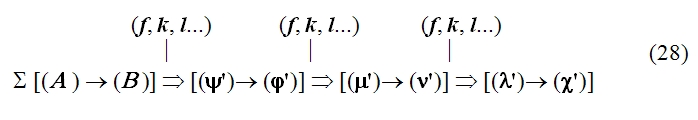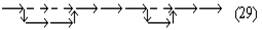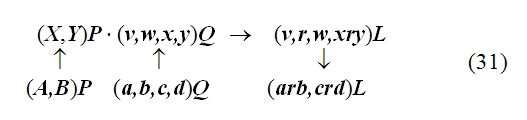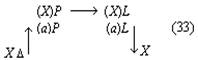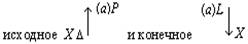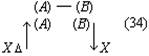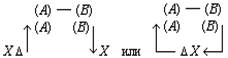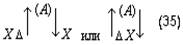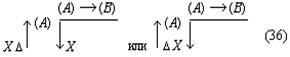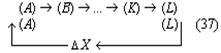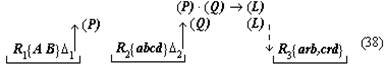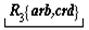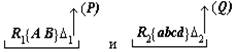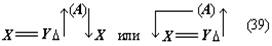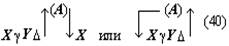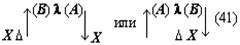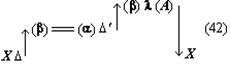|
Светлой памяти П. А. Шеварева посвящается. Наброски к предисловию:
Г. П. Щедровицкий, 24 сентября 1978 года. |
|||||||||||
1Очень часто мыслительный процесс решения какой-либо задачи выступает перед исследователем — логиком или психологом — в виде определённого знакового текста. Этот текст всегда, в принципе, является сложным образованием, то есть состоит из целого ряда определённым образом связанных между собой частей. Поэтому исследовать его — это значит также (наряду с другим) выделить эти части и найти связи между ними. В традиционной логике были выработаны определённые способы разложения речевых текстов на части. Это, во-первых, способ, основанный на понятиях суждения и умозаключения в классической Аристотелевой логике, и, во-вторых, способы разложения, основанные на понятиях новой, так называемой «математической», или «символической», логики, в первую очередь на понятии высказывания и логических операций (скажем, таких, как конъюнкция, дизъюнкция и импликация). Однако — и в последнее время это всё более и более выясняется — эти понятия и основанные на них способы разложения языковых текстов непригодны для реконструкции и анализа собственно процессов мышления, выражающихся в этих текстах. Многочисленные соображения, служащие основанием для такого утверждения, могут быть сведены к двум основным положениям.
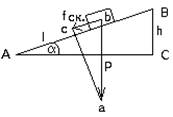
Последнее положение обычно вызывает недоверие и поэтому должно быть дополнительно разъяснено. Сравним для начала политэкономию Д. Риккардо или А. Смита с политэкономией К. Маркса. Стоя на позициях формальной логики, мы не найдём различий между этими работами. «Капитал» Маркса, как и сочинения Смита и Риккардо, состоит из суждений, умозаключений и систем умозаключений. И в то же время, Марксу удаётся решить проблемы, перед которыми Смит и Риккардо были бессильны. Например, буржуазная политэкономия до Маркса не могла разрешить антиномий: «товары продаются по их стоимости — товары не продаются по их стоимости», «прибавочная стоимость возникает в обращении — прибавочная стоимость не может возникнуть в обращении» и так далее, а Маркс разрешил их. Объяснить это можно только одним способом: Маркс мыслил иначе, чем Риккардо и Смит. Может ли быть отражено это различие в традиционных понятиях формальной логики, в понятиях суждения и умозаключения? Может ли быть отражено это различие в понятиях современной математической логики? Нет. И та и другая отнесут эти проблемы к области содержательных и тем самым исключат их из сферы своего исследования. Следовательно, чтобы уловить указанные различия, нужны другие понятия. Внимание логика должно быть сосредоточено на других сторонах мышления, нежели те, которыми занимаются классическая формальная и современная математическая логики. Разберём ещё несколько примеров, иллюстрирующих ограниченность понятий формальной логики в плане исследования мыслительных процессов. Представим себе, что учитель приносит на урок С точки зрения формальной логики это обычный полисиллогизм в форме энтимемы. В развёрнутом виде он может быть представлен в форме двух одинаковых силлогизмов первой фигуры. Вот, собственно, и всё, что можно сказать об этом рассуждении с позиций формальной логики. Представим себе далее, что ученику задана задача по физике: «Автомашина веса P движется вверх, на подъём, определяемый углом наклона a. Требуется узнать, какую мощность должен развить мотор автомашины, чтобы она могла двигаться вверх со скоростью v».
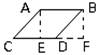
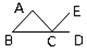
Ученику известно, что мощность машины N = Fv, где F = f ск. + f тр. (f ск. — скатывающая сила, f тр. — сила трения). Чтобы найти составляющие силы F, например f ск., ученик изображает величины P и f ск. векторами, а затем, установив подобие треугольников ABC и abc, находит, что f ск. /P = h/l, откуда f ск. = hP/l. Если мы попробуем представить этот процесс мышления в виде словесного рассуждения, то получим примерно следующее: «Мощность машины равна произведению движущей силы на скорость движения. — Движущая сила равна сумме сил скатывающей и трения. — Скатывающая сила может быть изображена вектором, направленным антипараллельно линии движения автомашины. — Как вектор, скатывающая сила, является составляющей вектора P, направленного к земле. — Векторы f ск. и P образуют стороны прямоугольного треугольника abc. — Стороны угла c в треугольнике abc параллельны сторонам угла C в треугольнике ABC. — Острые углы с соответственно параллельными сторонами равны. — Углы C и c равны. — Все прямоугольные треугольники с равными острыми углами подобны. — Треугольники ABC и abc подобны. — В подобных треугольниках отношения соответственных сторон равны. — Отношение f ск. к P равно отношению h к l. (И так далее)». Подходя с аппаратом понятий традиционной аристотелевой логики, мы, проделав некоторое насилие над суждениями об отношениях, фигурирующими в этом рассуждении, и представив их в атрибутивной форме, сможем разложить все приведённое рассуждение на ряд простых силлогизмов. На этом, очевидно, наше исследование должно закончиться. Подходя с аппаратом понятий логики отношений, мы разложим это рассуждение на ряд суждений об отношениях и сможем установить тип этих отношений. Но кого бы мы ни опросили — представителя традиционной аристотелевой логики или представителя логики отношений, — существует ли какое-либо формальное различие между двумя последними умозаключениями приведённого рассуждения? — они оба ответят отрицательно; как с точки зрения понятий Аристотелевой логики, так и с точки зрения понятий логики отношений никаких формализуемых различий здесь нет. Перейдём к следующему примеру. Перед исследователем эмпирически выявленная связь между объёмом и давлением газа. Её нужно объяснить. Для этого исследователь вводит понятие о внутреннем строении газа и понятие о молекулах, из которых он состоит. Каждый «удар» молекулы представляется как удвоенное произведение массы молекулы на её скорость, а давление газа — как результирующая «ударов» этих молекул, попадающих в единичную площадь стенки за единицу времени: P = S 2mivi. Если мы представим этот «кусочек» мыслительного процесса в форме словесного рассуждения, то получим примерно следующее: «Давление газа на стенку сосуда равно сумме «импульсов», отдаваемых всеми молекулами, ударяющими в единицу площади стенки за единицу времени. — Импульс, отдаваемый единичной молекулой, равен удвоенному произведению массы молекулы на её скорость. — Следовательно, давление газа на стенку равно сумме удвоенных произведений массы на скорость всех молекул, ударяющих в единицу площади стенки за единицу времени». Наконец, ещё один пример. В работе «Продуктивное мышление» известный немецкий психолог М. Вертхаймер приводит следующий случай. Он присутствовал на уроке в одной из лондонских школ, когда учитель объяснял как вычисляется площадь параллелограмма. Учитель нарисовал параллелограмм ABCD провёл вспомогательные линии AE и BF, показал, что треугольник CBF равновелик треугольнику DAE и что, следовательно, площадь параллелограмма ABCD равновелика площади прямоугольника ABFE и может быть определена как произведение основания на высоту, по формуле S = ah.
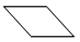
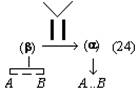
Ученики проработали заданный на дом материал — умели вывести эту формулу и решали по ней задачи. Однако Вертхаймер не был удовлетворён. Его интересовал вопрос, что же именно усвоили ученики, как они мыслили, насколько обобщённые представления и понятия у них сформировались. Чтобы получить ответ на этот вопрос, он предложил классу несколько видоизменённую задачу. Тот же самый параллелограмм был нарисован в другом положении.
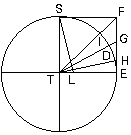
Надо было определить его площадь. «Многие ученики явно растерялись, — пишет М. Вертхаймер. — Один из них поднял руку: «Учитель нам этого не объяснял». Некоторые ученики срисовывали фигуру в свои тетради, проводили вспомогательные линии, но не могли доказать теоремы. Другая часть учеников выглядела ещё более несчастной: они подписывали под чертежом основную формулу S = ah, но не знали, как быть дальше. Когда я спросил, — замечает Вертхаймер, — могут ли они доказать теорему на этом чертеже, они отказались. Некоторые ученики перевёртывали тетради, проводили вспомогательные линии и сводили доказательство теоремы к ранее выученным примерам. Учитель, наблюдавший за учениками, сказал мне с оттенком неудовольствия: «Вы дали неправильную фигуру. Вполне понятно, что они не могут решить задачу» [Wertheimer 1945: 14–17]. Если мы будем представлять описанные Вертхаймером случаи в виде словесных рассуждений, то как для первого, так и для второго случая получим, И в то же время совершенно ясно — и растерянность учеников во втором случае наглядно подтверждает это, — что процессы мышления в указанных случаях чем-то отличались друг от друга. Но это различие носит такой характер, что, Теперь сравним между собой все приведённые выше примеры. С точки зрения формы, как её понимает формальная логика, — и мы уже об этом сказали — здесь особых различий нет. И в то же время легко заметить, что приведённые мыслительные процессы во многом отличны друг от друга. Возьмём хотя бы те два силлогизма, из которых складывается рассуждение в первом примере. Что является основанием для первой посылки первого силлогизма? Наблюдаемый на опыте эмпирический факт. Вторая посылка выражает общее знание, известное учащимся до начала опыта. Вывод представляет собой «включение» данного вещества в определённый класс или «подведение» его под понятие кислоты. Это знание составляет одну посылку второго силлогизма, вторую — общее знание. А вывод в этом, втором силлогизме — «приписывание» данному веществу определённых свойств, не обнаруженных в ходе опыта. Как видим, смысловая направленность этих частей рассуждения разная. Мы ещё более почувствуем эту разницу, если сравним первый пример со вторым. Ученик имеет описание Но, чтобы решить задачу, этих связей недостаточно. Ученик изображает данные ему величины векторами. Воспроизводит их пространственные взаимоотношения, устанавливает определённое отношение (подобие) между ними и другими пространственными величинами h и l, которые находятся в известном отношении между собой, и уже на основе всего этого определяет искомую величину. Ещё более отличается от разобранных третий пример. Здесь исследователь гипотетически вводит Наконец, четвёртый пример наглядно показывает, что за одними и теми же речевыми рассуждениями могут скрываться и скрываются весьма различные процессы мышления и что, следовательно, могут существовать такие процессы мышления, которые в самих речевых выражениях вообще никак не фиксируются и, следовательно, непосредственно не проявляются и поэтому непосредственно и не могут быть обнаружены. Легко заметить, что всё то, что мы сказали о недостаточности традиционных понятий формальной логики для анализа приведённых примеров, в полной мере справедливо и по отношению к понятиям современной математической логики. Поэтому в дальнейшем мы чаще всего будем говорить просто о понятиях формальной логики и будем подразумевать при этом не только традиционные понятия: «суждение», «умозаключение», «понятие», но и все понятия логики отношений и математической логики. Теперь мы можем сформулировать нашу собственную точку зрения. Приведённые выше примеры рассуждений принадлежат, очевидно, к различным видам мышления. Однако, если мы будем анализировать их в традиционных понятиях формальной логики или в понятиях логики отношений и математической логики, мы этого различия не уловим. А между тем наша задача — исследовать и отобразить в представлениях и знаниях основные закономерности мышления, в частности основные закономерности процессов решения задач, все те особенности и различия, которые необходимы для понимания реальных процессов мысленного познания, для управления ими. Кратко выражая этот вывод, мы и говорим, что существующие способы анализа сложных знаковых текстов (содержащих решение задач), основанные на понятиях формальной логики, непригодны для исследования собственно мыслительных процессов. Отсюда естественная задача: выработать такую систему исходных понятий, с помощью которой мы могли бы, анализируя речевые тексты и, в частности, разлагая их на части, в то же время реконструировать процессы мышления как таковые и представить их в их собственно мыслительной специфике. 2Но, поставив перед собой такую задачу, мы тотчас же сталкиваемся с проблемой метода. Ведь разложить всякое сложное целое на части можно по-разному, и поэтому в зависимости от того, какая задача стоит перед нашим исследованием, в зависимости от того, что мы, собственно, хотим исследовать, выявить, одни способы разложения будут правильными, адекватными данной задаче и предмету, а другие — неправильными, неадекватными. На это обстоятельство, используя очень яркий пример, указывал ещё Л. С. Выготский: «Нам думается, что следует различать двоякого рода анализ, применяемый в психологии. Исследование всяких психических образований необходимо предполагает анализ. Однако этот анализ может иметь две принципиально различные формы, из которых одна, думается нам, повинна во всех тех неудачах, которые терпели исследователи при попытках разрешить эту многовековую проблему «проблему отношений мышления и речи», а другая является единственно верным и начальным пунктом для того, чтобы сделать хотя бы самый первый шаг по направлению к её решению. Первый способ психологического анализа можно было бы назвать разложением сложных психических целых на элементы. Его можно было бы сравнить с химическим анализом воды, разлагающим её на водород и кислород. Существенным признаком такого анализа является то, что в результате его получаются продукты, чужеродные по отношению к анализируемому целому, — элементы, которые не содержат в себе свойств, присущих целому как таковому, и обладают целым рядом новых свойств, которых это целое никогда не могло обнаружить. С исследователем, который, желая разрешить проблему мышления и речи, разлагает её на речь и мышление, происходит совершенно то же, что произошло бы со всяким человеком, который в поисках научного объяснения каких-либо свойств воды, например почему вода тушит огонь или почему к воде применим закон Архимеда, прибег бы к разложению воды на кислород и водород как к средству объяснения этих свойств. Он с удивлением узнал бы, что водород сам горит, а кислород поддерживает горение, и никогда не сумел бы из свойств этих элементов объяснить свойства, присущие целому. Так же точно психология, которая разлагает речевое мышление в поисках объяснения его самых существенных свойств, присущих ему именно как целому, на отдельные элементы, тщетно потом будет искать эти элементы единства, присущие целому. В процессе анализа они испарились, улетучились, и ему не остаётся ничего другого, как искать внешнего механического взаимодействия между элементами, для того чтобы с его помощью реконструировать чисто умозрительным путём пропавшие в процессе анализа, но подлежащие объяснению свойства» [Выготский 1956: 46]. И далее: «Нам думается, что решительным и поворотным моментом во всём учении о мышлении и речи, далее, является переход от этого анализа к анализу другого рода. Этот последний мы могли бы обозначить как анализ, расчленяющий сложное единое целое на единицы. Под единицей мы подразумеваем такой продукт анализа, который, в отличие от элементов, обладает всеми основными свойствами, присущими целому, и который является далее неразложимыми живыми частями этого единства. Не химическая формула воды, но изучение молекул и молекулярного движения является ключом к объяснению отдельных свойств воды. Так же точно живая клетка, сохраняющая все основные свойства жизни, присущие живому организму, является настоящей единицей биологического анализа. Психологии, желающей изучить сложные единства, необходимо понять это. Она должна заменить методы разложения на элементы методом анализа, расчленяющего на единицы. Она должна найти эти неразложимые, сохраняющие свойства, присущие данному целому как единству, единицы, в которых в противоположном виде представлены эти свойства, и с помощью такого анализа пытаться разрешить встающие конкретные вопросы» (там же, с. 48). Мы полностью принимаем этот методологический принцип Л. С. Выготского. Но это тотчас же ставит перед нами целый ряд новых проблем. Во-первых, возникает вопрос, а можно ли таким образом разлагать мыслительные процессы, то есть не представляет ли собой каждый из них такого целого, которое обнаруживает свои специфические свойства только как целое, а ни одна из его частей, как бы мы их ни выделяли, этими свойствами уже не обладает. Не имея достаточно данных для обоснованного решения этого вопроса (мы вообще не уверены, могут ли существовать такие данные, помимо конечной удачи всего исследования), мы тем не менее примем гипотезу, что мыслительный процесс в общем случае может быть разложен на такие составляющие части, которые сохраняют специфические свойства мыслительного процесса, и всё дальнейшее исследование до определённого момента будем строить на этой гипотезе. Во-вторых, возникает вопрос, а какие собственно признаки являются специфическими признаками мыслительного процесса. Иначе этот же вопрос можно сформулировать так: а что такое процесс мышления? Отвечая на него, мы должны сконструировать определённую абстрактную модель процесса мышления, которая будет служить для нас «эталоном» для выделения таких процессов, или, иначе, для их реконструкции при анализе сложных языковых текстов. Но и этого мало. Сложные процессы мышления могут содержать в качестве своих частей (собственно говоря, так, Наконец, возникает вопрос: одинаковые ли стороны процессов мышления нужно выделять при эмпирическом анализе, когда в одном случае мы ставим перед собой задачу построить теоретическую систему функционирования мышления, а в другом — теоретическую систему развития его, или, может быть, для каждого из этих случаев нам понадобится своё особое эмпирическое разложение? Этот вопрос задаёт четвёртую методологическую проблему. Попробуем наметить пути решения этих проблем. 3Прежде всего необходимо выбрать единичные тексты для эмпирического анализа. Вообще говоря, они могут быть самыми различными, ибо разрабатываемый метод должен быть применим к любому и всякому тексту. Однако при реальном выборе текстов для анализа мы должны учитывать, что к чем более развитому «этажу» мышления будет принадлежать выбранный текст, тем больше сложных и свернутых структур знания будет содержать процесс мышления, выраженный в этом тексте, и тем больше, следовательно, будет затемняться собственно операциональная структура этого процесса структурами знания, движущимися в нём. Другими словами, к чем более развитому «этажу» мышления будет принадлежать выбранный текст, тем труднее нам будет в нём разобраться без предварительной выработки понятий о соответствующих структурах знаний. И поэтому для начала мы должны выбрать такие тексты и соответственно такие процессы мышления, которые были бы, с одной стороны, достаточно сложными, чтобы в них можно было выявить необходимое разнообразие операций и способов их сочленения, а с другой, — чтобы структуры движущихся в этом процессе знаний были бы достаточно простыми. Затем нужно обратить внимание на то, чтобы выбираемый текст был цельным, а не частичным. Отобрать цельный текст можно «по смыслу», иначе сказать, по пониманию содержания: он должен, с одной стороны, не быть непосредственно связанным с другими текстами, а с другой — обладать неразрывной внутренней связностью, то есть быть таким, чтобы ни одно из входящих в него предложений не могло быть выброшено без ущерба для всего текста. Первоначально выбор цельного текста производится исключительно по интуиции и в целом ряде случаев — без труда. Но, чтобы сделать эту процедуру анализа научной в точном смысле этого слова, необходимо её осознать и выразить в точных понятиях. Поскольку выделение текста производится на основе Эта задача была поставлена уже в древнегреческой науке (Аристотелевы категории) и потом постоянно обсуждалась и «дорабатывалась» на протяжении всей истории философии. Теории категорий в онтологии, метафизике, теории познания и логике — все это различные попытки выработать перечень или систему таких содержательных характеристик. В результате накоплено очень много эмпирических перечислений, классификаций, описаний, однако строгих и продуктивных методов решения проблемы, несмотря на долгую её историю, так и не было выработано. Все предложенные описания, и в особенности системы категорий, выглядят исключительно спекулятивными, ненаучными; правильность выделения тех или иных характеристик в качестве категориальных, полнота их перечисления, связи между ними — все это кажется случайным. Объясняется такое положение, на наш взгляд, прежде всего господством порочного метода исследования языкового мышления, метода, основанного на принципе параллелизма формы и содержания. Следствием применения этого метода была невозможность выяснить, что же представляет собой содержание мышления, а следовательно, и невозможность исследовать виды или, скорее, типы содержания в их необходимой связи друг с другом. Чтобы построить систему содержательных характеристик языкового мышления, необходимо стать на принципиально иную, значительно более широкую точку зрения: нужно определить и вывести само содержание как то, что возникает в ходе взаимодействия общественного человека с объективным миром. Только такой подход даст необходимое научное основание для решения указанного вопроса и избавит нас от спекуляций фихтевско-гегелевского типа. Но сам этот подход возможен только при определённом плане построения исследования — при так называемом генетическом восхождении — и не может быть применён при анализе эмпирически заданных единичных языковых текстов. Кроме того, необходимым условием генетического восхождения является определённый минимум знаний о мыслительных процессах, полученный посредством эмпирического анализа. Поэтому прежде всего мы должны поставить вопрос о том, как можно использовать уже накопленный эмпирический материал о содержательных характеристиках языкового мышления для выработки новых понятий о мыслительной деятельности. Здесь, как нам кажется, на помощь может прийти понятие задачи. Каждый мыслительный процесс возникает в связи с определённой задачей, и его конечный продукт — определённое мыслительное знание — выступает как решение этой задачи. Поэтому можно сказать, что между конечным продуктом мыслительного процесса — знанием — и задачей, на решение которой этот мыслительный процесс направлен, существует известное соответствие; во всяком случае, продукт мыслительного процесса с В ряде психологических работ, связанных с исследованием мыслительной деятельности, задача определялась как характеристика отношения между целью и условиями; цель, в свою очередь, отождествлялась с сознаванием продукта деятельности. Такое понимание задачи не подходит нам по трём причинам. Во-первых, будучи связанным с понятием цели, оно и само приобретает сугубо субъективный характер и поэтому становится непригодным для чисто объективного анализа текстов. Во-вторых, оно опирается на заданность условий, хотя в целом ряде случаев именно поиск таких условий является основным ядром самих мыслительных процессов, и он, следовательно, не может быть охарактеризован этим понятием. В-третьих, такое понятие задачи объединяет в себе характеристики как конечного результата процесса мысли, так и того, с чего этот процесс начинает, его условий и «исходного материала»; изменение любого из этих моментов меняет и характеристику задачи. Это обстоятельство затрудняет сопоставление тех бесспорно генетически связанных между собой процессов мышления, которые имеют один и тот же конечный продукт — знание, но исходят из разных условий и поэтому, естественно, имеют разное строение. Учитывая эти моменты, мы сознательно отходим от принятого в психологических работах понимания задачи и отождествляем её (на первом этапе своего анализа) с определёнными, логически обобщёнными характеристиками продуктов мыслительных процессов, то есть конечных знаний. Чтобы иметь возможность классифицировать различные тексты на основе понятия о задаче, надо попытаться представить все существующие содержательные характеристики знаний — возможных конечных продуктов мыслительных процессов — в виде перечня логически обобщённых задач исследования (первоначально весьма приблизительного и условного). В соответствии со всем вышесказанным — и это важно подчеркнуть ещё раз — этот перечень «задач» будет представлять собой не что иное, как перечень категорий (это и есть логические типы знания, характеризуемые прежде всего со стороны их содержания). Поскольку задачи характеризуются со стороны содержания, появляется возможность в ряде пунктов определённым образом «организовать» этот перечень исходя из зафиксированных уже в исследовании объективных взаимоотношений соответствующих содержаний. (Нельзя забывать, что эта организация является пока очень приблизительной и во многом даже просто условной, фиксирующей некоторые чисто интуитивные и ещё совсем рефлексивно не проанализированные различения; она может быть уточнена и получит своё действительное обоснование только на втором этапе исследования мышления, в генетическом восхождении.) Чтобы только пояснить, что мы имеем в виду, говоря о перечне логически обобщённых задач, перечислим некоторые возможные различения. Можно, например, различить два типа системных предметов — чувственно-единое целое и чувственно-множественное целое. Первое характеризуется тем, что оно воспринимается как одно целое, а его элементы не воспринимаются совсем, второе — тем, что в виде самостоятельных целостных объектов воспринимаются его элементы, а само оно в своей совокупной целостности воспринято быть не может. Примером целых второго типа может служить капитал как система буржуазных производственных отношений. Каждая из этих задач определяет особое направление и особый план исследования. Вторым шагом может быть различение двух возможных типов изменения сложных предметов: процессов функционирования и процессов развития. Воспроизведение в мысли каждого из этих процессов становится самостоятельной задачей исследования. В сочетании с первым различением это даёт уже четыре возможных направления и соответственно четыре способа исследования. Если далее мы возьмём, к примеру, чувственно-единый предмет вне процессов изменения, то можно указать пять возможных направлений или задач его исследования и соответственно типов получаемого знания. Во-первых, можно поставить перед собой задачу исследовать отдельные «внешние», атрибутивные свойства этого предмета, то есть свойства, присущие ему как самостоятельному, изолированному целому. Во-вторых, можно исследовать зависимости, связи, существующие между этими свойствами. В-третьих, можно рассмотреть заданное сложное целое в качестве элемента или части ещё более сложного целого и поставить перед собой задачу выявить те отдельные связи или свойства-функции, внутри которых исследуемый нами предмет существует в этом более сложном целом. В-четвёртых, можно исследовать зависимости между этими связями или свойствами-функциями. Наконец, в-пятых, можно направить исследование на внутреннее строение заданного целого, поставить перед собой задачу выявить те элементы, «единички» или частички, из которых оно сложено, определить связи между ними и на этой основе рассмотреть внешние атрибутивные свойства рассматриваемого предмета и связи между ними как проявления его внутреннего строения. Внутри первого из указанных направлений можно, в свою очередь, выделить две различные задачи: исследование качественных и исследование количественных характеристик отдельных атрибутивных свойств. Внутри пятой задачи точно так же можно различить исследование состава рассматриваемого сложного целого и исследование его структуры. Продолжая этот процесс далее, мы получим в конце концов перечень задач исследования, которые будут достаточно дифференцированы и в то же время настолько общи, что их можно будет рассматривать как логически обобщённые. 4Имея подобный перечень задач исследования и вместе с тем перечень конечных продуктов процессов мышления, мы можем определённым образом охарактеризовать каждый встречающийся нам текст и выраженный в нём процесс мысли. Но одного этого определения процессов мысли по их продуктам, как мы уже мимоходом отмечали выше, недостаточно для однозначной характеристики этих процессов. Чтобы их охарактеризовать однозначно, нужно задать ещё исходную «точку», или исходный материал, и достаточное число промежуточных точек, которые описывали бы с необходимым приближением, образно говоря, «траекторию» процесса. Но такая постановка вопроса, на первый взгляд очень естественная и, можно даже сказать, единственно возможная и необходимая, наталкивается при анализе «движений» (процессов) на определённые трудности. Дело в том, что выделение исходных и промежуточных точек представляет собой легкую и естественную задачу только в том случае, когда мы рассматриваем линейное, неразветвлённое, непрерывное и гладкое образование. Если же эти требования не выполнены, то оказывается, что у исследуемого явления масса различных исходных точек, разнообразные способы соединения частей процесса в одно целое, причудливые скачки и переломы в «траектории», и так далее. Всё это требует при описании своих специальных понятий и крайне затрудняет первые эмпирические расчленения: не зная возможных особенностей анализируемых процессов, — всех этих разветвлений, изломов, разрывов, — мы не можем их правильно расчленить. Но мы никогда не будем всего этого знать, если не произведём необходимые расчленения. Выход из этого положения заключается — как всегда — в том, чтобы произвести первое приблизительное расчленение, а затем, опираясь на его результаты, исправлять и уточнять сами принципы. Простейшая гипотеза, которая может быть положена в основание этого первого расчленения, такова. Перечень логически обобщённых задач исследования или конечных знаний можно рассматривать одновременно и как перечень возможных типов исходных знаний. Исходные знания, в свою очередь, опираясь на их понимание, можно будет представлять и интерпретировать как определённые предметы исследования. Можно предположить также, что процесс мысли заключается в переходе от одних знаний к другим, причём в исходном пункте имеется всегда одно и только одно знание. Тогда каждый выделенный текст можно будет характеризовать уже по двум точкам — исходному знанию и конечному. Этот шаг можно будет рассматривать как переход к понятиям, характеризующим собственно мыслительную деятельность. Всякое рассуждение, всякий, если можно так сказать, «кусок», или «отрезок», зафиксированного в тексте рассуждения, исходящий из определённого предмета исследования (и вместе с тем — из знания определённого логического типа) и направленный на решение определённой (то есть логически определённой) задачи, можно будет обозначить как процесс мышления, или просто процесс, и зафиксировать в особом знаке. Таким образом (это важно отметить для дальнейшего), процесс мышления пока будет определяться как обычно — по фиксированным «состояниям», по продуктам, но при этом будут указываться две «точки», между которыми процесс осуществляется: во-первых, задача, которую он должен решить, или его продукт, результат, во-вторых, условия, в которых он применяется, то есть «логический материал», на который он направлен, из которого он исходит и который он преобразует. Поэтому сам процесс выступит как нечто отличное от продуктов, лежащее вне них и не соответствующее ни одному из них в отдельности. Тем самым будет уничтожена всякая возможность установления простого, непосредственного изоморфизма между продуктами мышления — знаниями — и порождающими их процессами. Другими словами, рассматривая процесс мышления как нечто связывающее между собой две группы явлений — исходный материал, куда входят также и знания, и конечное знание — и обозначая его особым языковым знаком, мы выделим особую действительность, отличную от действительности знаний как таковых. Вместе с тем мы введём более сложные понятия, предполагающие дополнительные приёмы исследования по сравнению с теми, которые необходимы для введения понятий о знаниях, и эти новые понятия о процессах мышления в каком-то плане «снимают», элиминируют понятия о знаниях. Но всё это является лишь началом анализа процессов мышления как таковых. Большинство из них представляет собой сложные образования, которые могут быть расчленены на составляющие элементы-процессы. Для этого внутри первоначально выделенных в качестве процессов мышления рассуждений нужно найти «промежуточные» задачи и соответственно промежуточные «конечные результаты» и «исходные пункты». Например, чтобы выделить и исследовать структуру какого-либо сложного объекта, надо предварительно выделить и исследовать его элементы. Поэтому в определённых процессах мышления эта последняя задача может оказаться промежуточной по отношению к задаче исследования структуры. Чтобы определить отношение между количественными характеристиками одного свойства двух каких-либо объектов, надо предварительно определить сами эти количественные характеристики, и в ряде процессов мышления эта последняя задача окажется промежуточной относительно задачи определения отношения. Но кроме промежуточных задач этого рода, то есть уже вошедших в перечень возможных содержательных задач исследования, в сложных процессах мышления обнаруживаются промежуточные задачи также и другого рода. Так, например, чтобы определить числовое значение отношения двух величин, недоступных непосредственному измерению, мы «переводим» это отношение в отношение других величин, доступных измерению, и, определяя последнее, тем самым определяем и первое. Задача переведения одного отношения в другое в таком процессе мышления выступает как промежуточная по отношению к задаче определения исходного отношения. Или другой пример. Чтобы определить числовую величину какой-либо характеристики геометрической фигуры (периметра, площади, и так далее), часто бывает необходимо включить её в качестве элемента в систему более сложной фигуры. Задача включения исследуемого предмета в какую-либо систему в таких процессах мышления является промежуточной по отношению к первой задаче. Промежуточными задачами такого же рода являются: «упрощение» рассматриваемого предмета, «сведение» его к другому предмету, «выведение» из другого, «отображение» одного предмета в другом и ещё целый ряд подобных задач. Все они дают возможность выделять составляющие процессы в сложных процессах мышления. Однако по характеру своему, «по природе» они значительно отличаются от задач первого рода. Для первых специфическим признаком служит характеристика типа содержания, фиксируемого в знании, являющемся продуктом соответствующего процесса. Вторые же не могут быть поняты с точки зрения такой характеристики: например, переведение исследуемого отношения двух величин в такое же по своему числовому значению отношение других величин бессмысленно с точки зрения содержательных задач первого рода. Точно так же включение рассматриваемого предмета в более сложную систему есть просто переход к другому предмету, к исследованию этого другого предмета — переход, неоправданный с точки зрения задач первого рода. И тем не менее такие процессы мышления существуют и играют огромную роль в процессах исследования. Если не выделить и не зафиксировать в особом перечне задачи этого рода, то будут совершенно непонятными и выпадут из исследования значительные и существенные части реальных процессов мышления. Действительное значение и смысл задач второго рода раскрываются только во второй части исследования — в восхождении, при сопоставлении содержательной задачи исследования, традиционных средств её решения и условий, в которых находится предмет. Но выделение этих задач необходимо уже в первой части исследования — при эмпирическом расчленении языковых рассуждений. Такое выделение может быть осуществлено путём сопоставления различных промежуточных знаний, получаемых в ходе сложного процесса мышления. Именно из этого сопоставления мы получаем определения задач — переведение, упрощение, включение в систему, сведение, выведение, и так далее. Оно характеризует отношение между исходным и конечным знаниями для отдельных частей исследования и вместе с тем место и функциональную роль этих частей исследования в сложном процессе мышления. Последовательное применение такого анализа процессов мышления, то есть выделение промежуточных задач исследования (первого и второго рода) и разложение процесса на составляющие части в соответствии с выделенными задачами, должно в конце концов привести нас к таким процессам мышления, которые таким способом уже не могут быть разложены на составляющие. Такие, далее неразложимые этим способом анализа, или элементарные с точки зрения этого способа, процессы мышления мы будем называть операциями мышления или просто операциями. Разлагая процессы мышления на составляющие их операции, мы в то же время будем фиксировать последовательность и связь этих операций в каждом исследованном процессе. Сопоставление проанализированных таким образом процессов мышления между собой позволит нам выделить чаще всего встречающиеся комбинации операций, что может служить намёком на существование связи между ними. Фиксированный таким образом эмпирический материал должен быть затем объяснён во второй части исследования мышления — в «восхождении». Рассматривая операции, составляющие сложные процессы мышления, и типы связей между этими операциями, мы переходим в новую и почти неразработанную область исследования мыслительной деятельности, в область исследования её строения. Строение (элементарный состав и структура) процессов мышления будет, очевидно, их третьей — наиболее важной и притом специфически процессуальной — характеристикой. Разлагая таким образом различные процессы мышления, мы будем получать все новые и новые операции. Однако, с другой стороны, мы будем встречаться и с уже выделенными ранее операциями. Хотя отдельные части существующего в настоящее время совокупного знания весьма отличаются друг от друга, а следовательно, отличаются друг от друга и процессы мышления, посредством которых это знание было получено, тем не менее всё оно может быть разбито на сравнительно небольшое число частей, внутри которых знание имеет одну и ту же логическую характеристику и получается посредством одних и тех же «способов» исследования. Например, такие задачи исследования, как воспроизведение структуры исследуемого предмета или процессов функционирования системы объекта, процессов развития системы объекта, и так далее, задают способы исследования и все процессы мышления, посредством которых решаются эти задачи в применении к различным объектам. Анализируя указанным выше путём, то есть путём разложения на операции, различные процессы мышления, входящие в один способ исследования, мы сможем, Перечень всех операций мышления, выделенных в том или ином способе исследования, мы будем называть «алфавитом операций» этого способа. После того как существующие в настоящее время способы исследования будут в общем и целом проанализированы и будут найдены их алфавиты операций, встанет задача сравнить последние между собой и выделить абстрактный алфавит операций, общий для всех процессов мышления и соответственно для всей логики. 5Такой или примерно такой, как это изложено в предыдущем разделе, представляется схема эмпирического анализа языковых текстов, если мы примем первую простейшую гипотезу относительно строения выраженных в них процессов мышления, а именно будем предполагать, что процессы эти представляют собой строго линейные, неразветвлённые, непрерывные и гладкие переходы от одного знания к другому знанию. Но сама эта гипотеза с самого начала была задумана лишь как первое приближение к предмету, как понимание, мало похожее на действительное. Предполагалось, что попытки произвести подобное расчленение реальных текстов натолкнутся на трудности, но это вместе с тем даст нам материал для дальнейших уточнений самой гипотезы, для более глубокого понимания действительного строения процессов мысли и изменения принципов анализа. Чтобы осуществить эту работу, мы взяли один достаточно сложный текст и попробовали его анализировать. Текст представлял собой изложение рассуждений Аристарха Самосского (III век до Новой эры), посредством которых он определил отношение расстояний «Солнце — Земля» и «Луна — Земля». Вот это изложение: «Аристарх нашёл, что когда видна половина лунного диска, угол между Солнцем и Луной содержит 87 градусов. Но когда половина освещённой части Луны обращена к Земле, линии, соединяющие центр Луны с центрами Солнца и Земли, перпендикулярны. Таким образом в треугольнике, вершины которого в центрах Солнца, Луны и Земли, все углы известны; следовательно, можно определить отношение гипотенузы к катету, то есть отношение расстояний Солнца и Луны от Земли. Вот как Аристарх определил это отношение: пусть Т есть центр Земли, L — центр Луны и S — центр Солнца, что соответствует первой четверти Луны, так как SL ^ TL.
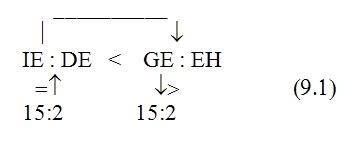
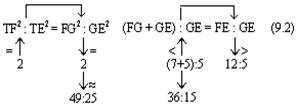
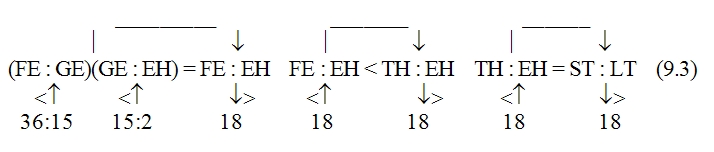
Согласно наблюдениям Аристарха дуга SD содержит 87 градусов, следовательно, дуга DE содержит З градуса. Проведем линию TG под углом в 22½° к TE. Тогда, так как 22½° = ¼ d, а 3° = ⅓0 d, то отношение дуг IE и DE будет IE: DE = ¼: ⅓0 = 15/2; но отношение отрезков GE и EH больше отношения дуг, и, значит: GE: EH> IE: DE GE: EH> 15:2 Квадрат, построенный на диагонали TF, вдвое более квадрата, построенного на TE или EF. Но в D ETF линия TG — биссектриса угла ETF, поэтому TF: TE = FG: GE, следовательно, квадрат, построенный на FG, вдвое более квадрата, построенного на GE, то есть отношение квадратов, построенных на этих линиях, немного более 49/25, поэтому отношение прямых FG и GE немного более 7/5, откуда отношение FE: GE 12:5, или, что то же, FE: GE 36:15. Но мы видели, что GE: EH 15:2, стало быть, FE: EH 18, или EH менее 1/18 FE, а так как FE TH, то EH менее 1/18 FE и менее 1/18 TH. Из подобия треугольников SLT и TEH следует, что EH: TH = LT: ST, откуда LT менее 1/18 ST. Аналогично Аристарх доказывает, что LT более ½0 ST, и заключает, что расстояние Солнца от Земли превышает расстояние Луны от Земли не более чем в 20 раз и не менее чем в 18 раз» [Попов 1932: 91–92] 1. Приведённая совокупность предложений представляет собой одно целостное рассуждение, или один целостный «языковой текст», так как все эти предложения объединены одной задачей и в своём итоге дают одно (искомое) значение. Именно потому, что нас интересуют не особенности языковой формы рассуждения, а его логическая структура, мы могли взять и рассматривать не оригинальный текст самого Аристарха, а любое переложение его, лишь бы оно достаточно точно повторяло те переходы от одного знания к другому, которые содержались в оригинале, а не слишком модернизировало их за счёт применения структур знания, возникших позднее. К этому тексту был применён анализ, соответствующий изложенным выше принципам. Мы не можем здесь излагать все ходы — удачные и неудачные — и детали этого анализа; это заняло бы несоразмерно много места. Изложим лишь некоторые рассуждения и их результаты, имеющие общее и принципиальное значение. 6Прежде всего выясняется, что если продукт (или конечное знание) рассматриваемого процесса мысли определяется сравнительно легко — это положение о том, что расстояние Солнца от Земли превышает расстояние Луны от Земли не более чем в 20 и не менее чем в 18 раз, — то исходный материал, или исходные знания, с которых начинает этот процесс, напротив, определить не так-то просто. И дело здесь заключается в следующем. «Естественным» условием решения задачи такого типа, как та, которая встала перед Аристархом Самосским — найти математическое отношение величин двух расстояний, — является знание числовых величин самих сопоставляемых расстояний. Тогда, на том уровне развития знаний, на каком находился Аристарх, процесс мышления был бы исключительно простым. Если говорить точнее, в этом случае вообще не нужно было бы никакого процесса мышления в собственном смысле этого слова: задача могла бы быть решена посредством «чисто формальной» арифметической операции деления. Однако пойти таким путём Аристарх Самосский не мог, так как числовые величины расстояний, отношение которых нужно было найти, были ему неизвестны и определить их непосредственно он не мог. Именно это обстоятельство и заставило Аристарха «мыслить», то есть строить определённый процесс рассуждения. Это построение мы и будем анализировать, но предварительно должны разобрать одно весьма важное и уже отчётливо выступившее здесь обстоятельство, поясняющее, почему трудно сразу же определить исходный материал разбираемого сложного процесса мышления. Мы сказали, что на том уровне развития знаний, на каком находился Аристарх Самосский, если бы были известны числовые значения сопоставляемых расстояний, задача могла бы быть решена посредством «чисто формальной» арифметической операции деления, без помощи собственно мышления. Но тем самым мы косвенно указали на то, что существуют и другие уровни развития мышления, такие, на которых эта задача не может быть решена формально и требует собственно процесса мышления. И действительно, такой уровень не так уж трудно себе представить. Ведь был период, когда не умели делить одни числовые величины на другие, когда не была выработана и не стала «формальной» и вместе с тем механически осуществляемой операция деления. Чтобы решить подобную задачу, то есть чтобы получить число, определяющее во сколько раз «величина» одного явления или предмета больше или меньше «величины» другого явления или предмета, на том уровне развития мышления надо было осуществить определённый и весьма непростой процесс мышления. Затем, с переходом на другой, более высокий уровень мышления дело меняется, и Аристарх, как мы уже сказали, мог бы решить задачу без всякого процесса мышления, посредством формальной операции деления. Но условием осуществления такой операции является целая система знаний, а именно знаний частных от деления одних величин на другие. И если продумать это обстоятельство до конца, в частности если проанализировать природу формальных операций, входящих в каждый сравнительно высоко развитый процесс мышления, то придётся признать, что при анализе мало-мальски сложных процессов мышления понятие исходного материала, или — что то же — исходного знания, с которого начинает процесс, оказывается уже недостаточно чётким и определённым. И дело здесь отнюдь не в субъективных неточностях или ошибках, которые мы могли допустить в определении этих понятий. Причина этой неопределённости лежит значительно глубже: в объективной сложности самих реальных процессов мышления. Понятие исходного материала абсолютно правильно и верно, но оно слишком абстрактно для анализа высокоразвитых процессов мышления. Только самые простые операции мышления имеют в качестве исходного материала одно какое-либо знание, и только в этом случае сами эти операции таковы, что это знание является для них действительно исходным, то есть они перерабатывают его в другое знание. Когда же мы переходим к более сложным операциям и процессам мышления, то оказывается, что, кроме одного исходного знания в собственном смысле этого слова, то есть знания, «перерабатываемого» в другое, они предполагают в качестве условий своего осуществления ещё целый ряд других знаний, которые «включены» в сам процесс мышления, и — что принципиально важно — перестраивают его, превращают в другой или другие процессы, а в конце концов делают вовсе не процессом мышления, а формальными действиями. Если взять разбираемый случай, то такой системой знаний в простейшем случае является таблица частных от деления разных чисел друг на друга 2. Действия деления как формальные действия возможны только при наличии такой системы общественно фиксированных и запоминаемых индивидами знаний. Включаясь в различные более или менее сложные процессы мышления, эти знания превращают различные составляющие этих процессов в формальные действия и тем самым перестраивают сами эти процессы. Но в силу этого эти знания оказываются таким же исходным материалом для перестроенных сложных процессов мышления, как и те знания, которые собственно перерабатываются в этом процессе. Во всяком случае, они определяют характер процесса мышления, хотя и по-другому, но ничуть не в меньшей степени, чем последние знания. Если бы этих знаний не было, то процесс мышления имел бы совершенно другой состав и совершенно другую структуру. Таким образом, в сложных процессах мышления исходный материал не исчерпывается каким-то одним знанием. В него входит много и притом, как приходится постоянно убеждаться в ходе анализа, разнообразных по своей логической функции знаний. Чтобы правильно проанализировать строение различных процессов мышления, мы должны выделить и проанализировать все эти логические функции знаний. Только в этом случае наши методологические понятия станут достаточно конкретными. Но чтобы сделать это с достаточной полнотой, необходимо осуществить процесс восхождения от абстрактного к конкретному. А пока мы можем только различить в исходном материале собственно исходные знания, которые перерабатываются данными операциями или процессами мышления в другие знания, и — как мы будем условно говорить — «краевые» знания, «краевой» исходный материал, подразумевая под этим те знания, которые делают возможными сами эти операции и процессы мышления. Специально следует отметить, что различение собственно исходных и краевых знаний позволяет в Взаимоотношение этих двух планов исследования поднимает целый ряд сложных вопросов, но сейчас мы не можем их обсуждать и вернёмся к ним ниже. Итак, первый вывод, к которому мы приходим при попытке анализа конкретного текста на основе изложенных выше принципов: процесс мышления содержит неоднородные части — содержательные процессы и формальные операции. Наличие формальных операций существенным образом меняет процесс получения определённого продукта и при этом по-разному — в зависимости от того, какие это формальные операции. Эта неоднородность, а точнее, именно наличие формальных операций меняет само строение исходного материала и наше понятие о нём; в исходном материале приходится различать собственно исходные знания, которые в ходе процесса перерабатываются в другие знания, и краевые знания, которые, оставаясь неизменными, определяют характер этой переработки. Эта двойственность исходного материала и его историческая относительность являются одной из причин, затрудняющих его выделение при анализе конкретных текстов. 7Второй корректирующий вывод, который мы должны сделать, заключается в том, что отнюдь не все процессы мышления являются линейными. В частности, анализируемый нами процесс решения задачи Аристархом, как выясняется, включает процессы мышления, направленные, образно говоря, перпендикулярно друг к другу. Чтобы убедиться в этом, проследим за процессом решения задачи дальше. Итак, мы выяснили, что, имея указанную выше систему формальных арифметических знаний, Аристарх Самосский мог бы решить поставленную задачу посредством чисто формальной операции деления. Но для этого нужно было знать числовые значения сопоставляемых расстояний. А Аристарх их не знал и, более того, не мог узнать с помощью традиционной операции измерения. Такое положение вещей создавало проблему и требовало мышления. Выражая этот факт в понятиях нашего содержательного анализа, мы можем сказать, что рассматриваемый процесс мышления как бы повисает в воздухе. Он оказывается без собственно исходного материала, который — и это очень важный результат анализа — ещё только должен быть найден. Это последнее положение, не определяя исходного знания рассматриваемого процесса мышления, равно как и самого этого процесса, в то же время — при определённых дополнительных условиях — даёт возможность найти «промежуточную задачу», которая должна быть решена, чтобы можно было решить исходную задачу, и вместе с тем — также при определённых дополнительных условиях — даёт возможность определить те процессы мышления, которые в качестве составляющих частей должны войти в состав исследуемого процесса. Одной из возможных промежуточных задач было бы определение расстояний «Земля — Солнце», «Земля — Луна». И в настоящее время можно построить процессы мышления, посредством которых эта задача решается. Однако во времена Аристарха Самосского не было ни знаний, необходимых для этого, ни соответствующих приёмов и операций мышления. Поэтому Аристарху пришлось идти совершенно иным путём, использовать иные приёмы и операции мышления. Вместо того чтобы определять по отдельности расстояния LT и ST и затем находить их математическое отношение, Аристарх устанавливает, что это отношение (как единое целое) равно другому математическому отношению, а именно EH:TH, и на основании известного ему численного значения последнего определяет искомое отношение LT:ST. Чтобы выделить процессы и операции мышления, заключённые в этом рассуждении, мы должны, в соответствии с общими принципами метода, найти в заданном тексте то знание, от которого Аристарх переходит к знанию о математическом отношении расстояний «Земля — Солнце» и «Земля — Луна». Однако наша попытка тотчас же наталкивается на целый ряд затруднений. Прежде всего оказывается, что в рассматриваемом тексте имеется по крайней мере два предложения, которые могут претендовать на роль таких знаний. Это, во-первых, предложение «EH:TH =LT:ST» и, во-вторых, предложение «EH менее 1/18 TH». С точки зрения принципов, намеченных выше, в процессе мышления может быть только одно собственно исходное знание, а второе — если оно обнаруживается — должно быть краевым. Однако попытка применить это последнее понятие в том виде, как оно было сформулировано выше, к данному случаю вызывает возражения. Дело в том, что понятие краевого знания было введено для обозначения тех знаний, которые лежат в основе формальных действий, являются общественно фиксированными логическими связями между обобщёнными содержаниями и безотносительны к тем или иным конкретным объектам. Но в данном случае ни одно из выделенных знаний не удовлетворяет этому требованию полностью. Знание «EH менее 1/18 TH», очевидно, является единичным и вырабатывается специально для данного конкретного случая. Знание «EH:TH = LT:ST» в определённом аспекте могло бы удовлетворить этому требованию: его выражение, или знаковая форма, представляет собой пропорцию, и в силу этого это знание служит основанием для ряда формальных действий, в частности для определения численного значения одной части пропорции по известному численному значению другой части или же для определения численного значения любого члена пропорции, если известны численные значения других членов, и так далее. Но с другой стороны, знание «EH:TH = LT:ST» в своём конкретном содержании не является общественно фиксированным знанием, безотносительным к единичным объектам, и должно вырабатываться специально для данного случая — с помощью особого процесса мышления, который должен входить в состав анализируемого сложного процесса. В силу этого нам приходится сделать вывод, что ближайшая часть анализируемого процесса мышления распадается на два относительно самостоятельных и в то же время особым образом, как бы «перпендикулярно», связанных друг с другом процесса мышления. Трудность здесь состоит в том, что обе обнаруживающиеся части слиты, спаяны в одном сокращённом, исключительно лаконичном рассуждении («EH менее 1/18 TH. Из подобия треугольников SLT и TEH следует, что EH:TH = LT:ST, откуда LT менее 1/18 ST»), а их надо разделить и рассмотреть относительно независимо друг от друга. И здесь, чтобы осуществить это разделение, мы хотим, несмотря на все приведённые выше оговорки, воспользоваться уже введённым понятием краевого знания, употребляя его, правда, в несколько более широком смысле, чем раньше, но в той же самой функции. Мы предположим, что знание «EH:TH = LT:ST» является краевым, что анализ процесса получения его в силу этого должен быть выделен в особую задачу и может пока не проводиться, и таким путём наметим «основную» линию процесса мышления — как движение между знаниями о математических отношениях EH:TH и LT:ST. Но тут обнаруживается второе затруднение. Даже при условии всех тех предположений и ограничений, которые мы выше сделали, выделенная часть языкового текста может рассматриваться в двух различных планах. Если судить непосредственно по структуре и порядку самого языкового текста, то движение мысли происходит от известного числового значения математического отношения EH:TH к известному значению математического отношения LT:ST. Иначе говоря, по значению первого мы определяем значение второго, или, ещё иначе, значение первого переносим на второе. Поэтому схематически этот процесс может быть представлен формулой (EH:TH) → (LT:ST) (1) где скобки означают, что мы имеем дело со знаниями, а стрелка — «направление» самого мыслительного перехода или мыслительного преобразования. Но в то же время нетрудно заметить, что в реальном мыслительном процессе, который должен был бы иметь место в условиях сформулированной выше задачи, порядок движения мысли должен быть обратным. Мы не знаем числового значения математического отношения LT:ST и непосредственно узнать его не можем, так как не знаем числового значения членов этого отношения. Но нам нужно решить задачу, и поэтому мы ищем (или создаём) Осуществление этого процесса предполагает прежде всего выбор или создание того отношения, которое мы будем определять в первую очередь и от которого затем будем двигаться к исходному. Это выбираемое среди уже имеющихся или вновь создаваемое математическое отношение должно удовлетворять двум требованиям:
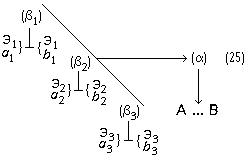
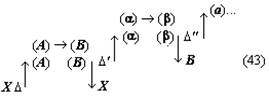
При этих условиях анализируемый процесс мышления выступает как замещение одного математического отношения другим, как подстановка одного отношения на место другого. Чтобы отметить, что здесь происходит замещение именно отношения двух величин другим отношением, мы условно будем называть этот процесс мышления «переведением». Заметим ещё раз: чтобы осуществить переведение одного математического отношения в другое, мы должны установить равенство (или какое-либо другое отношение, эквивалентное ему с точки зрения переведения) математических отношений LT:ST и EH:TH. Установление такого отношения представляет собой решение особой познавательной задачи и входит в качестве особого частичного процесса мысли в анализируемый сложный процесс. Но мы уже отделили его от основного процесса мышления, положив, что указанная задача является краевой для рассматриваемого нами процесса мышления, и мы можем поэтому пока не рассматривать этот частичный процесс мышления, предполагая, что его результат уже дан. Это позволит нам продолжать анализ процесса переведения как такового и его функциональной роли в рассматриваемом сложном процессе мышления. Осуществив процесс переведения, мы устанавливаем, что численное значение математического отношения LT:ST равно численному значению другого отношения, именно EH:TH. Но мы не устанавливаем самого этого численного значения, не знаем, чему оно равно, и, следовательно, не получаем искомого решения основной задачи. Чтобы получить это решение, мы должны либо определить числовые значения самих величин EH и TH, либо ещё раз перевести это математическое отношение в какое-либо другое или, если понадобится, в третье, четвёртое и так далее. Но сколько бы нам ни пришлось делать таких переведений — и этот момент очень важно отметить, — сами по себе эти процессы мышления не могут решить основной задачи — определения численного значения математического отношения, они только как бы «сдвигают» её, переносят её решение на другие математические отношения и объекты, создают иные условия для осуществления действия, непосредственно необходимого при получении числового значения какого-либо математического отношения. Это положение является принципиально важным для всего дальнейшего анализа заданного текста, и поэтому мы сформулируем его ещё раз со всей возможной резкостью: переведение, сколько бы раз оно ни осуществлялось, отнюдь не исключает необходимости непосредственного определения числовых значений величин, входящих в отношение; переведение только отодвигает это действие непосредственного определения. Но из этого, в частности, следует, что процесс переведения, сколь бы многошаговым он ни был, должен в конце концов упереться либо в знания числовых значений двух соотносящихся величин, либо в мыслительные операции, непосредственно дающие эти знания, либо в Исходя из этого положения, мы можем сразу же, не прибегая к детальному анализу промежуточных задач и составляющих процессов мышления, попробовать найти исходное знание рассматриваемого сложного процесса мышления. Для этого нужно только бегло обозреть анализируемый текст и найти среди входящих в него положений знания численных значений каких-либо величин, между которыми затем устанавливается математическое отношение. Такой обзор заданного рассуждения Аристарха сразу же показывает, что в нём имеются знания соответственно о трёх величинах: дуге SD («Согласно наблюдениям Аристарха дуга SD содержит 87 градусов»), дуге DE (это знание получается путём простой операции мышления, анализ которой мы сейчас опускаем; математически это: 90° — 87° = 3°) и дуге IE (последняя задаётся построением: «проведём линию TG под углом в 22½° к TE»). Между дугами IE и DE затем устанавливается математическое отношение. Таким образом, мы выясняем, что знания о величине дуг SD и IE или при упрощённом рассмотрении — дуг IE и DE являются исходными знаниями в рассматриваемом сложном процессе мышления. Тогда в простейшем случае анализируемый текст может представлять собой последовательность переведений исходного отношения LT:ST в известное со стороны своего численного значения отношение IE: DE через ряд других, промежуточных отношений. Но это может быть и более сложный случай, в котором переведения — а Подобно тому как первый «шаг» анализируемой нами мысли оказался состоящим из двух частей — основной и краевой (в расширенном значении), — связанных друг с другом как бы «перпендикулярно», так и все последующие «шаги» процесса обнаружили в грубом приближении точно такое же строение. Но это значит, что и весь процесс мысли по решению исходной задачи оказался отнюдь не линейным, а имеющим — при данном анализе — причудливое строение, которое приблизительно можно изобразить так:
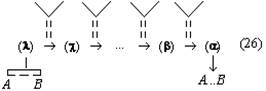
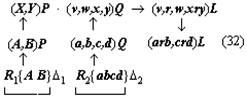
(скобки изображают отношения, в которые последовательно переводится искомое, а стрелки — выделяемые при таком анализе составляющие процессы мысли). 8Третий вывод, к которому мы приходим в ходе анализа выбранного текста, может быть выражен примерно так: процессы мысли могут иметь не только основную и краевую части, но и распадаться на ряд «ветвей», как бы соединяющихся в одной точке. Каждая из этих ветвей имеет свои основную и краевую части. Действительно, рассмотрим следующие шаги анализируемого процесса. Мыслительная операция (или процесс), следующая за переведением математического отношения LT:ST в отношение EH:TH, в первом приближении тоже может быть охарактеризована как переведение: от математического отношения EH:TH мы с её помощью переходим к математическому отношению EH:FE. Однако нетрудно обнаружить, что это переведение имеет свои специфические и, Саму эту замену, или подстановку, мы производим не в силу установления определённого соотношения между этими математическими отношениями как целыми, а в силу того, что мы устанавливаем определённое соотношение между двумя изолированными величинами («… так как FE TH…»), одна из которых является членом этого отношения. Хотя конечный результат рассматриваемого процесса мышления кажется таким же, как и в предыдущем случае, однако знание, которое выступает в данном случае в качестве краевого, имеет существенно иной характер, а поэтому и весь процесс мышления, включая его вторую, краевую ветвь, будет значительно отличаться от первого. Не анализируя сейчас детально эту часть процесса мышления, а вместе с тем специфическую сторону всего процесса в целом, мы просто отметим это различие, чтобы вернуться к нему в дальнейшем, и будем называть эту разновидность переведения (или, может быть, принципиально иной процесс мышления) подстановкой элемента. Но что мы делаем далее с математическим отношением EH:FE? К какому мыслительному процессу прибегаем? Члены этого отношения непосредственно не определяются. Попытка применить к соответствующей части текста понятие переведения тоже не даёт результата. Дело в том, что математическое отношение EH:FE мы получаем исходя не из одного, а из двух других отношений. Мы знаем, с одной стороны, что FE:GE 36:15, с другой, — что GE:EH 15:2, и, комбинируя эти отношения в соответствии с определёнными формальными правилами, получаем нужное нам значение математического отношения EH:FE. Таким образом, мыслительного процесса переведения здесь нет. Но что представляет собой этот процесс? Его условием является целая система знаний о неравенствах и правилах оперирования с ними. Эти знания могут быть рассмотрены как краевые в узком смысле этого термина, и исследование мыслительных процессов, с помощью которых они формируются, будет таким образом вынесено за границы исследования данного текста. Но кроме этого круга вопросов существует ещё целый ряд других — не менее важных, которые не могут быть вынесены за рамки анализа данного текста. Именно здесь, в этом месте мы сталкиваемся с тем, что анализируемый текст разделяется на две ветви, и ни одну из них нельзя, Все эти вопросы оставим пока нерешёнными и попробуем продвинуться дальше в анализе каждой ветви этого текста. Одна из них оказывается весьма коротким и по своему характеру уже известным нам процессом мышления. Это — переведение математического отношения отрезков GE:EH в математическое отношение дуг IE:DE, численное значение которого уже известно, то есть переведение в отношение, непосредственно определяемое по исходным знаниям. Основанием для этого переведения служит установление определённого соотношения (GE:EH IE:DE), но по установившемуся уже методу мы выносим соответствующий процесс мышления за пределы данного плана анализа, пользуясь понятием краевой задачи и краевого процесса (в широком смысле этого слова). Вторая ветвь оказывается значительно более длинным и по своему характеру значительно более сложным процессом мышления. Сложным прежде всего потому, что он в значительно большей мере пронизан ссылками на «геометрические» положения и собственно «геометрическими» рассуждениями. В проанализированных ранее частях текста тоже были такие ссылки и рассуждения, но там нам удалось вынести их в область краевых процессов и таким путём избавиться от их непосредственного анализа при рассмотрении основной мыслительной линии текста. Здесь, в этой ветви текста, положение иное: геометрические положения и рассуждения играют столь важную роль и занимают такое положение, что отнести их к краевым процессам часто оказывается уже невозможным. Но из этого, в частности, следует, что достаточно полный и продуктивный анализ соответствующего процесса мышления невозможен без анализа общей природы и специфических моментов геометрического знания и геометрического рассуждения. Если все же, несмотря на все эти оговорки, попробовать осуществить анализ этой ветви текста по уже выработанной схеме, то строение соответствующей части процесса мышления представится в нижеследующем виде. Конечным продуктом всей этой части процесса является знание «FE: GE 36:15». Исходными знаниями — положения: «TF — диагональ квадрата», «TE и FE — стороны квадрата», «квадрат, построенный на диагонали TF, вдвое более квадрата, построенного на TE или EF». Третье положение получается из двух первых на основе геометрических положений, и, чтобы проанализировать соответствующий процесс мышления, мы должны предварительно проанализировать природу «геометрического мышления». Для упрощения положим, что исходным является знание об отношении: «квадрат, построенный на TF, вдвое более квадрата, построенного на TE». Тогда, так как конечное знание является знанием о математическом отношении и исходное знание тоже является знанием об отношении, мы можем предположить, что процесс мышления, их связывающий, представляет собой серию переведений. В В этом плане выделенный нами процесс оказывается новинкой. Основанием для перехода от одного математического отношения к другому в нём оказывается весьма сложное соотношение «TF:TE = FG:GE». И сложными здесь являются как способ связи этого основания с самими математическими отношениями (от соотношения отрезков мы переходим к соотношению площадей квадратов, построенных на них), так и процесс мысли, посредством которого мы получаем само это основание: он включает в себя целый ряд геометрических соображений и положений («… в D ETF линия TG — биссектриса угла ETF, поэтому TF:TE = FG:GE…»). И если при этом процесс выработки соотношения-основания мы можем назвать краевым и вынести за границы основного процесса мысли, то с переходом от этого основания к переводимым математическим отношениям так поступить нельзя: он составляет ядро основного, анализируемого процесса мысли. В то же время суть его составляют собственно геометрические соображения, и поэтому здесь он не может быть проанализирован в достаточной мере. Следующий переход, входящий в рассматриваемый текст, — от отношения квадратов, построенных на линиях FG и GE, к отношению самих этих линий. Краевым для него является знание об отношении между величиной площади квадрата и величиной его стороны. Наконец, последняя составляющая часть этой ветви процесса мышления — переход от отношения FG:GE к отношению FE:GE. Чтобы осуществить его, надо учесть, что FG и GE — части одной прямой FE (знание, получаемое из анализа чертежа), определить величину этой прямой и затем уже, учитывая, что относительные числовые значения отрезков получены при сопоставлении с одним эталоном, составить новое отношение: «FE:GE 12:5». При формальном обратном движении, то есть уже в изложении, этот переход может быть осуществлён посредством чисто формальных преобразований пропорций, фиксированных в соответствующей системе знаний: x:y = a:b → (x + y): y = (a + b):b (4). Но эти знания, так же как и переход, совершаемый в соответствии с ними, являются уже продуктом определённого процесса мышления, который необходимо проанализировать. Пока, однако, как его условия, так и его строение остаются совершенно неясными. 9Прежде чем переходить к формулированию дальнейших методических коррективов, попробуем резюмировать проделанный уже анализ и свести его результаты в одну схему. Приступая к решению этой задачи, мы прежде всего должны отметить то обстоятельство, что заданный процесс содержит целый ряд относительно обособленных от основной линии частичных мыслительных процессов, которые мы обозначили как краевые (в широком смысле этого слова). По своему строению это весьма различные процессы мысли (мы пока не анализировали, какие именно), но у них у всех (это то, что нам сейчас особенно важно) очень сходные продукты: знания о соотношениях, позволяющие замещать один «элемент» соотношения другим или, поскольку «элементами» в заданном процессе мышления в большинстве случаев являются математические отношения, переводить один «элемент» в другой. Если рассмотреть каждый из этих частичных мыслительных процессов сам по себе, с точки зрения его «внутренней природы», то окажется, что он никак не связан с другими краевыми процессами. Например, процесс установления соотношения «EH:TH = LT:ST» по своей собственной природе никак не связан с процессом установления соотношения «FE:EH TH:EH», который как краевой процесс следует непосредственно за ним в сложном процессе мышления. Процесс установления соотношения «FE:EH TH:EH», в свою очередь, по своей природе не связан с осуществляемым рядом с ним краевым процессом установления соотношения «GE:EH IE:DE». (Собственно говоря, именно это обстоятельство — отсутствие такой непосредственной связи между процессами, когда продукт одного становится исходным материалом для другого, — и позволило нам определить их как краевые.) Но хотя между указанными частичными краевыми процессами и нет непосредственной, вытекающей из их собственной «природы» связи, тем не менее в рассматриваемом сложном процессе мышления все они связаны между собой в одно целое. То, что их объединяет, и то, ради чего все они здесь осуществляются, есть задача переведения исходного математического отношения LT:ST в Если попробовать выразить взаимоотношение этих задач и процессов мышления схематически, то в простейшем случае оно будет выглядеть примерно так:
В верхнем ряду этой схемы записаны знания о соотношениях, получаемые посредством краевых процессов; k:l, e:f и так далее — элементы этих соотношений, причём k:l есть исходное математическое отношение, численное значение которого нужно определить, а a:b — математическое отношение, численное значение которого известно или легко может быть определено и в которое в конечном счёте переводится исходное отношение. Вертикальные стрелки с индексами (I), (II), (III) в схеме обозначают процессы мышления, посредством которых вырабатываются знания о соотношениях, то есть собственно краевые процессы мышления. Штриховые стрелки над верхним рядом схемы условно обозначают задачу и направление процессов переведения. Представленная таким образом эта схема наглядно показывает, что процессы переведения и процессы установления соотношений между элементами k:l, e:f, a:b идут как бы «в различных направлениях» и что именно переведение есть та задача, которая в данном случае определяет общую схему всего процесса в целом, последовательность и порядок всех его звеньев. Кроме всего прочего, эта схема заставляет нас сделать ряд важных методологических выводов. Она показывает, что в сложных процессах мышления существует особый тип связи частичных процессов мысли, а именно связь через отношение их продуктов — знаний — к другой задаче, лежащей как бы в ином направлении и определяющей основную линию процесса. Указанный момент является, на наш взгляд, обстоятельством первостепенной важности, требующим самого пристального внимания в дальнейшем исследовании. Намеченная выше схема является, как мы уже сказали, схемой самого простого случая. Поэтому естественно, что она во многих пунктах не соответствует рассматриваемому конкретному процессу мышления. Но все эти отклонения эмпирически данного процесса от схемы могут быть рассмотрены как дальнейшие усложнения самой этой схемы и поэтому совсем не отменяют принципов, указанных выше. В частности, остаётся неприкосновенной идея непрерывной последовательности соотношений верхнего ряда и краевых процессов получения этих соотношений, идущих как бы «перпендикулярно». Наибольшая часть отклонений объясняется тем, что в разбираемом процессе «горизонтальное» движение не исчерпывается одними переведениями, а включает в себя также целый ряд иных процессов, например «подстановку элемента», «комбинирование двух соотношений» (FE:GE 36:15, GE:EH 15:2) и другие; все эти процессы, однако, полностью укладываются в усложнённую схему «цепи соотношений» с двумя ветвями. Если произвести некоторые упрощения, а в одном соотношении (GE:EH =FE:EH) модернизацию 3 и преобразование соответствующего процесса мышления, то схема рассуждения Аристарха будет выглядеть примерно так 4:
Как и в схеме (5), вертикальные стрелки здесь изображают краевые процессы мышления, а штриховые стрелки над формулами соотношений условно намечают линии переведения. Штриховые линии со звездочками (а их всего три: одна в основной линии и две во второй ветви) обозначают иные, нежели переведение, процессы мышления; нетрудно заметить, что по функции и по продукту эти процессы мало чем отличаются от переведения: выработанные с их помощью знания входят в ту же цепь соотношений. 10Схема 6 позволяет отчётливее понять и делает чуть ли не наглядным ещё один исключительно важный момент, который заставляет нас сделать ряд выводов, ревизующих исходные принципы. Речь идёт, во-первых, о направленности процесса мышления, а во-вторых, о соотношении формальных и содержательных моментов в нём. Рассмотрим это подробнее. Соотношения, устанавливаемые процессами (I), (II), (III) …, обусловливают, как мы уже не раз отмечали, возможность переведения исходного математического отношения в другие, уже известные. Но после того, как эти соотношения установлены, процесс переведения не осуществляется. Вместо него мы осуществляем другой процесс, который условно может быть назван «переносом». Перенос в сопоставлении с переведением характеризуется двумя моментами Во-первых, это движение, по направленности своей противоположное переведению: если при переведении мы идём от исходного неизвестного к известному, то при переносе мы, напротив, движемся от известного к неизвестному. Во-вторых, если переведение, по идее, должно быть процессом прежде всего содержательным 5 (хотя оно и может содержать в качестве фрагментов формальные действия), то перенос в противоположность этому является действием прежде всего формальным, то есть совершаемым, как говорят, «по формуле», в соответствии с уже установленной связью знаний (хотя в ряде случаев он может содержать в качестве фрагментов содержательные, неформализованные действия) 6. Именно этот второй процесс — перенос, а не переведение — выражается, как правило, в языковом тексте при изложении материала. И в этом можно убедиться с первого же взгляда. Например, в анализируемом рассуждении Аристарха Самосского «отношение дуг IE к DE будет IE:DE = ¼:⅓0 = 15:2. Но отношение отрезков GE и EH больше отношения дуг, и, значит: GE:EH IE:ED, GE:EH 15:2». Или в другом месте этого же рассуждения: «Отношение FE:GE 12:5, или, что то же, FE:GE 36:15. Но мы видели, что GE:EH 15:2, стало быть FE:EH 18, или EH менее 1/18 FE, а так как FE TH, то EH менее 1/18 FE и менее 1/18 TH». Если изобразить порядок движения в одном действии переноса схематически, то он для простейшего случая будет выглядеть примерно так:
Здесь a обозначает численное значение математического отношения а:b, уже известное или определяемое с помощью какого-либо мыслительного действия или процесса; вертикальная стрелка (I) обозначает движение (или фиксирующую его знаковую связь) при приписывании этого значения математическому отношению а:b; стрелка над соотношением а:b = с:d — формальный перенос значения a с отношения a:b на отношение с:d, а вертикальная стрелка (II) — результат всего этого переноса, приписывание значения a непосредственно математическому отношению c:d 7. Несколько следующих друг за другом действий переноса мы, используя эту схему, должны будем изобразить так:
Рассуждение Аристарха Самосского, изображённое в этих схемах, будет иметь вид 8:
Итак, мы выяснили, что задача переведения какого-либо математического отношения в другое математическое отношение порождает новую задачу: установить определённое соотношение между этими математическими отношениями. Соотношение это устанавливается специально для целей переведения и, естественно, должно быть таким, чтобы это переведение можно было осуществить. Но после того как такое соотношение установлено, процесс переведения уже не осуществляется; вместо него мы осуществляем противоположно направленный формальный процесс переноса. Этот факт на первый взгляд выглядит парадоксальным, но он не должен вызывать удивления. Как общий вывод мы должны сформулировать положение, что выработка и включение в процессы мышления знаний о соотношениях существенным образом меняет строение и механизм самих этих процессов. И это, Но такой вывод заставляет нас вернуться к начальному пункту анализа и вновь поставить вопрос о том, какие же именно знания, выделяемые в рассматриваемом языковом тексте, мы можем рассматривать как исходные для действительного процесса мышления, а какие — как конечные для этого процесса. По сути, мы вновь возвращаемся к основному вопросу нашего метода — о способе задания и выделени я процессов мышления. Если бы в качестве действительного процесса мышления мы взяли процесс переноса, то начальные наши характеристики — математического отношения ST:LT как конечного знания, а математического отношения TH:EH как исходного — были бы правильными. Но так как мы пришли к выводу, что перенос есть деятельность прежде всего формальная и, чтобы иметь возможность осуществить её, надо предварительно, исходя из задачи (определить отношение LT:ST), найти другое (уже известное или ещё неизвестное) математическое отношение, с помощью которого можно было бы найти первое, то, казалось бы, естественно предположить, что действительный процесс мышления — переведение — идёт как бы в противоположном направлении, и поэтому начальные характеристики исходного и конечного знания нужно просто «перевернуть», назвав математическое отношение ST:LT исходным знанием, а математическое отношение TH:EH — конечным. Но и такой подход тоже оказывается ложным. Во-первых, потому, что задачу (найти математическое отношение ST:LT) нельзя рассматривать как исходное знание, и наш предполагаемый процесс мышления остаётся, следовательно, без исходного знания. Во-вторых, математическое отношение TH:EH, если брать его изолированно, само по себе, тоже не может рассматриваться как конечное знание. Необходимым условием переведения ST:LT в TH:EH является знание об их равенстве (или установление соотношений «больше», «меньше»); поэтому можно сказать, что конечным знанием искомого действительного процесса мышления является знание о равенстве математического отношения ST:LT математическому отношению TH:EH. Но здесь, как это ни странно, мы приходим к парадоксальному с точки зрения исходных понятий метода положению. Точно так же, как знание о равенстве отношений ST:LT и TH:EH является необходимым условием переведения, знание о необходимости переведения, или задача переведения, является необходимым условием процесса мышления, направленного на установление равенства между математическими отношениями ST:LT и TH:EH. Иначе говоря, до тех пор пока мы не поставим задачу переведения одного отношения в другое, мы не можем поставить задачу установить соотношение равенства между ними. Но, с другой стороны, поставив задачу переведения, мы не осуществляем соответствующего ей процесса мышления, а «переходим» к другой задаче. Подобно этому мы можем затем перейти к третьей задаче, не осуществляя процесса мысли, непосредственно соответствующего второй задаче, к четвёртой, не осуществляя процесса мысли, соответствующего третьей, и так далее. После же того как вторая (или третья и так далее) задача решена и соответствующее значение получено, происходит «возвращение» к первой (или второй и так далее) задаче, но такое возвращение и при таких условиях, которое делает ненужным процесс мышления, необходимый в других условиях для решения этой задачи, как бы отменяет его и заменяет другим, формальным действием. Этот факт, на наш взгляд, имеет первостепенное теоретическое значение. Прежде всего потому, что он совершенно В этой связи тотчас же возникает целый ряд вопросов.
11Наметив весь этот круг необходимо возникающих здесь теоретических вопросов, мы можем вернуться назад, к анализу процессов переведения и переноса и соотношения между ними и наметить ещё один исключительно важный тезис. Указанное выше изменение процесса мышления — замена содержательного процесса переведения формальным переносом — не является единственным. Та же самая причина — выработка знаний о соотношениях — создаёт условия и для другого изменения процесса мышления. Каждое из соотношений устанавливается для того, чтобы можно было осуществить один определённый «шаг» переведения и делает возможным один обратный ему «шаг» формального переноса. И если бы все исходные задачи мышления могли быть решены с помощью одного такого шага переведения, а все соответствующие части процессов мышления исчерпывались одним шагом переноса, то последний всегда осуществлялся бы именно так, как это изображено на схеме 7. Но поскольку в большинстве процессов мышления, так же как и в разбираемом примере, таких переведений (или аналогичных им процессов) целый ряд, поскольку с помощью краевых процессов мышления устанавливается непрерывная цепь соотношений, постольку процесс формального переноса, а вместе с тем и процесс мышления в целом существенным образом меняются. Установленные соотношения как бы обособляются от каждого отдельного акта переноса конкретного числового значения с одного математического отношения на другое. К ним применяется иная формальная деятельность, а именно деятельность по преобразованию последовательной цепи соотношений в одно соотношение. Если изображать движение мысли в этом случае схематически, то оно будет выглядеть примерно так:
Где вертикальные стрелки (I) и (II), как и прежде, обозначают непосредственное приписывание числовых значений соответственно математическим отношениям a:b и k:l; стрелка над соотношениями обозначает формальный перенос, округлые линии 1 и 2 — формальные преобразования цепи соотношений в одно соотношение. Если исключить эти последние преобразования и сразу взять их конечный результат, то схема соответствующего процесса мысли примет вид:
То есть сведётся к одному простейшему шагу переноса. Чтобы осуществить это сведение, надо, как мы уже сказали, предварительно проделать целый ряд особых формальных действий, преобразующих цепь соотношений в одно соотношение. В разбираемом рассуждении из этих действий осуществляются только немногие, и поэтому Аристарху приходится не один раз переносить конкретные численные значения одних математических отношений на другие, а много раз. Чтобы свести разбираемое рассуждение к одному переносу, надо было бы проделать следующие формальные преобразования:
Последнее соотношение, полученное в преобразовании (18), представляет собой «сокращение» всей цепи соотношений; в левой его части стоят только известные математические отношения:
А в правой — исходное, определяемое математическое отношение ST:LT. Получив это сокращённое соотношение, мы можем решить исходную задачу путём простых арифметических вычислений и одного действия переноса. При некоторых упрощениях схема процесса мышления, осуществляющегося в этом случае, будет выглядеть примерно так:
Нетрудно заметить, что записанная выше система преобразований Преобразования 16 и 17, в свою очередь, очень напоминают традиционное определение. Сейчас, в нашем плане рассмотрения, несущественно, что преобразования Многие представители традиционной логики считают действия или операции, посредством которых осуществляются эти преобразования, процессами мышления; и более того, нередко они полагают, что этими действиями мышление и исчерпывается. Проведённый выше анализ рассуждения показывает, что действия такого типа, как те, которыми осуществляются преобразования 12–18, отнюдь не исчерпывают процессов мышления. Более того, этот анализ показывает, что указанные действия и операции возникают лишь в результате двукратного изменения процесса мышления, обусловленного выработкой общих знаний о соотношениях, что они являются лишь одним из следствий этого изменения и одним из условий осуществления процесса мышления (в данном случае — переноса) в новой, сокращённой форме. Можно сказать даже резче: мыслительные действия и операции, осуществляющие преобразования Это не значит, что эти формальные действия и операции не надо исследовать при изучении мышления. Совсем нет. Но это значит, что их надо исследовать именно как часть процессов мышления и притом как часть отнюдь не главную, а только подсобную, вспомогательную и поэтому вторичную, что их надо изучать после того, как изучены основные, определяющие процессы мысли, и — с точки зрения последних. Но основными, определяющими мыслительными процессами являются процессы, порождающие задачи такого типа, как переведение, процессы, посредством которых вырабатываются общие знания о соотношениях (в своём анализе мы выделили их как краевые), наконец, те изменения, которые происходят с процессами мышления, после того как выработаны общие знания о соотношениях. Пока мы наметили два таких изменения. И мы можем повторить здесь то, что говорили выше по поводу одного из них: Основываясь на том, что уже изложено, мы можем поставить целый ряд вопросов, относящихся к этому исследованию.
В этой части работы мы не можем дать ответ на эти вопросы: решение их требует систематического восходящего исследования. Нам важно только сформулировать эти вопросы, показать, что они естественно возникают из содержательного анализа реальных, эмпирически данных мыслительных рассуждений, и тем самым поставить задачу для дальнейшего исследования. Поскольку это сделано, цели данной части работы достигнуты, и мы можем продолжить анализ не затронутых до сих пор частей рассуждения Аристарха Самосского, имея в виду выделить и сформулировать новые поправки к намеченным вначале принципам. 12До сих пор, анализируя процесс мышления, скрывающийся за выбранным нами текстом, мы выделяли в так называемые краевые процессы все те отрезки мышления, посредством которых устанавливаются соотношения между исходным математическим отношением (численную величину которого нужно определить) и другими отношениями, в конечном счёте уже известными. Мы выделяли их из так называемой основной линии и оставляли без анализа. Однако на этом пути выяснилось, что именно в этих, оставленных без внимания краевых процессах заключено, Мы предполагали также, что краевые процессы непосредственно между собой не связаны (собственно, это предположение и давало нам право выделять их из основной линии и оставлять пока без внимания) и что поэтому мы можем рассматривать их по отдельности, вне какого-либо определённого порядка. Но какой бы краевой процесс заданного рассуждения мы ни взяли, мы всюду наталкиваемся на одно и то же затруднение общего порядка; точно охарактеризовать это затруднение без введения дополнительных логических понятий трудно, но можно сказать так: применение особых графических средств. Возьмём в качестве примера самый первый (с точки зрения переведения) краевой процесс — установление соотношения «EH:TH = LT:ST». В тексте Аристарха он выражается одной лаконичной фразой: «Из подобия треугольников SLT и THE следует…». У читателя, подходящего к этому выражению с логической точки зрения и знающего пока только исходную задачу, это выражение сразу же должно вызвать вопрос: какие треугольники? Перед Аристархом две планеты — Солнце и Луна, и он хочет определить отношение их расстояний до Земли. Вот, казалось бы, и всё, что объективно дано в ситуации задачи. Откуда же берутся треугольники? Отвечая на этот вопрос, мы должны принять во внимание, что в дополнение к тому, что дано в ситуации задачи, Аристарх Самосский вводит ещё нечто. Это нечто, как мы уже сказали, трудно охарактеризовать: его можно назвать «чертежом», «моделью пространственных соотношений», «системой геометрических фигур», и так далее. Но как бы мы его ни называли, важно, что это нечто является для Аристарха ничуть не менее объективным, чем расстояния «Земля — Солнце» и «Земля — Луна»; поэтому его можно ещё назвать «дополнительным объектом». Аристарх как бы «накладывает» созданный людьми объект на объективные пространственные отношения, заданные ему ситуацией задачи, «сопоставляет» созданную людьми систему геометрических фигур с объективными расстояниями «Земля — Солнце», «Земля — Луна» и затем, осуществив это «наложение», или «сопоставление», начинает определённым образом действовать с этой искусственно созданной системой фигур, преобразовывать её и таким путём решает исходную задачу, относящуюся к расстояниям «Земля — Солнце» и «Земля — Луна». Указанное сопоставление и последующие действия с системой геометрических фигур и являются соответственно тем актом мышления, который необходимо исследовать. Два основных вопроса, на которые должны быть получены ответы в этом исследовании, суть следующие:
Необходимость дать ответы на эти вопросы заставляет нас обратиться к исследованию геометрии и, если можно так сказать, «геометрического» мышления, то есть мышления в геометрии и с помощью средств геометрии. Ещё раз повторим, что мы никак не можем излагать здесь все или даже все основные ходы этого исследования и вынуждены будем дать лишь основные соображения и выводы из них. Первый из этих выводов может быть сформулирован так: геометрические чертежи суть одновременно и знаки особого специфического языка, и объекты исследования. Этот тезис направлен, по существу, против всех существовавших до сего времени концепций. Вплоть до последней четверти ХIX века исследователи геометрии — философы, логики, историки науки — почти единодушно считали, что изображения фигур или чертежи в геометрическом доказательстве служат только для одной цели — для образования наглядных представлений — и что мышление в геометрии, соответственно, исходит из результатов созерцания этих фигур, «обрабатывает» дальше эти результаты, или, другими словами, что мышление в геометрии строится на основе чувственного созерцания. Начиная с последней четверти ХIХ века в связи с работами по формализации геометрии, предпринятыми Э. Бельтрами, Г. Грассманом, Ф. Клейном, Д. Пеано, М. Пиери, М. Пашем, Д. Гилбертом и другими, философы, логики и математики начали усиленно доказывать обратное — что геометрия вовсе не нуждается в наглядных представлениях, а вместе с тем и в чертежах, что она может и должна быть построена на понятиях, выраженных предельно символически и не нуждающихся для своего образования ни в каких интуитивно-созерцательных моментах. Однако вся их борьба шла прежде всего по линии суммарного отрицания предшествующего тезиса, по линии чистого противоположения, и до самого последнего времени, насколько мы знаем, большинство исследователей не приходило к мысли отказаться от предвзятого взгляда на чертежи как на наглядные представления и поставить вопросы: а чем чертежи являются на самом деле? что они собой представляют? какую роль играли прежде в «геометрическом» мышлении и какую роль играют теперь? Одной из причин, мешавших такой постановке вопроса, было широкое распространение плоско-сенсуалистического понимания мышления как способа отражения, не непосредственно связанного с объектами, а как бы надстраивающегося над чувственным «наглядным» отражением и, в соответствии с этим, связанного с объектами через посредство чувственного отражения. Примерно к 1930-м — Этот взгляд на природу чертежей геометрии является значительным шагом вперёд по сравнению с плоско-сенсуалистическим пониманием их как моделей или продуктов наглядного представления (уже хотя бы потому, что В определённом отношении и с определённой точки зрения геометрические чертежи действительно могут выступать и выступают как знаки языка. Обычно, однако, к этому добавляют: как своеобразного языка, как языка особого рода. В чём причина такой всегда присутствующей оговорки? Что скрывается за ней? В чём своеобразие этого языка, или иначе: чем он отличается от других языков? И здесь, при ответе на этот вопрос, мы вновь сталкиваемся с тем свойством геометрических фигур, которое раньше характеризовалось как их наглядность. Но теперь мы должны рассмотреть и объяснить эту сторону принципиально иначе. Вдумываясь в проблему с новых позиций, мы прежде всего видим, что тезис о наглядности можно весьма просто понять как трансформированное, извращённое представление одной реальной особенности геометрических фигур. Любые математические, химические или просто словесные символы, взятые сами по себе, также наглядны, как и геометрические чертежи 10. Поэтому когда специально говорят о наглядном характере последних и выделяют это как их особое, специфическое свойство, то имеют виду, очевидно, нечто иное, нежели наглядность как таковую. Чтобы сделать эту мысль предельно понятной и отчётливой, воспользуемся следующим примером. Представим себе, что какой-либо человек, желая сообщить другому человеку, сколько у него баранов в стаде, передаёт последнему мешочек с зернышками проса, количество которых точно соответствует количеству баранов в стаде 11. В этой ситуации зернышки проса являются не чем иным, как знаками (своеобразного!) языка: не только в этой, но и в целом ряде других ситуаций с их помощью успешно решаются задачи отражения и коммуникации, наличие их даёт возможность производить целый ряд практических действий, например, обмен баранов на что-либо другое, и так далее. Представим себе далее, что в силу каких-либо обстоятельств такая форма выражения количества баранов в стаде нас уже не устраивает и мы хотим, используя полученный мешочек с просяными зернышками, выразить это количество в форме числа. Для этого мы, естественно, должны будем пересчитать зернышки. Пусть их будет, к примеру, 30. «30» есть тоже знак языка, и притом — своеобразного языка, языка арифметики. Но как знак он существенно отличается от просяных зернышек. С зернышками проса, являющимися знаком количества баранов в стаде, мы действуем во второй ситуации так же, как действовали бы с самими баранами: и тех, и других мы пересчитываем. Но это означает, что совокупность зернышек, несмотря на то, что она является знаком количества баранов в стаде, обладает реально тем же свойством количества, что и совокупность баранов. С числом «30», тоже выражающим количество баранов в стаде и тоже являющимся знаком этого количества, так действовать уже нельзя: его можно складывать с другим числом, можно из него вычитать другое число, его можно умножать, делить, возводить в степень, из него можно извлекать корень, но его нельзя пересчитывать. Это доказывает, что знак «30», взятый сам по себе, не обладает реально количеством, не содержит в себе этого свойства, он только обозначает это количество. Иначе, более строго, этот же вывод можно сформулировать так: с точки зрения действия пересчёта мешочек с просяными зернышками является таким же объектом, как и само стадо баранов, а число «30» с точки зрения этого действия пересчёта таким «количественным» объектом не является. Чтобы придать этому положению действительно правильный смысл, необходимо сделать ещё несколько уточняющих замечаний. 1.Положение о том, что просяные зернышки с точки зрения познавательной деятельности являются такими же объектами, как и замещаемые ими бараны, нисколько не противоречит положению о том, что совокупности этих зернышек являются каждый раз знаками определённых количеств баранов. Будучи с точки зрения операции пересчёта такими же объектами, как и сами бараны, просяные зернышки во многих других отношениях существенно отличаются от баранов (их, например, можно носить в мешочке за поясом, чего нельзя сделать с баранами, изменение количества просяных зернышек в мешочке в принципе всецело зависит от человека, в то время как количество баранов в стаде часто меняется независимо от воли человека, и так далее), и это обстоятельство служит тем основанием, которое позволяет сделать зернышки проса знаками баранов, несмотря на их тождество как определённых, реальных количеств. Поскольку зернышки проса — это не бараны, действие их пересчёта, если рассматривать его в ситуации, где нас интересуют именно бараны, само по себе, вне той замещающей функции, которую эти зернышки выполняют по отношению к баранам определённого стада, является совершенно бессмысленным, никчемным. Другими словами, в заданной ситуации нас совершенно не интересуют зернышки проса сами по себе, и мы интересуемся вопросом, сколько их в мешочке, только для того, чтобы таким путём узнать, сколько в стаде баранов. Таким образом, действие пересчёта просяных зернышек в описанной ситуации имеет смысл только в связи с действием замещения зернышками проса самих баранов, только в структуре более сложной деятельности, включающей замещение. Но это означает, что действие пересчёта зернышек проса в ситуации, когда нас интересуют бараны, оставаясь по способу выполнения тем же самым действием, что и пересчёт самих баранов, действием, направленным на предметы реальной совокупности и оперирующим непосредственно с этими предметами, по функции своей является другим действием, нежели пересчёт самих баранов, — действием, направленным на объекты-заместители. Поэтому такое действие пересчёта, учитывая его функцию, можно назвать «замещающим». Резюмируя изложенное выше, можно сказать так: если с точки зрения характера деятельности пересчёта, взятой изолированно, зернышки проса в мешочке являются такими же объектами, как и сами бараны, то с точки зрения 2.Сравнивая две формы выражения определённого количества — другое такое же количество и число — и выяснив, что к числу не может быть приложена специфическая деятельность пересчёта, мы сделали вывод, что, следовательно, оно не обладает свойством «количественности», или, что то же, не является реальным количественным объектом. В этой связи могут возразить, что существует другая деятельность, к примеру, сложение или умножение, в контексте которой число выступает как «представитель» и «носитель» количества как такового и, следовательно, с точки зрения этой деятельности есть такой же количественный объект, как и совокупность зернышек проса или бараны. Но такая мысль была бы ложной, так как просяные зернышки или баранов в стаде нельзя ни складывать (в точном смысле этого слова и этого действия), ни умножать. Таким образом, с точки зрения операций сложения или умножения число, к примеру, «30» действительно выступает как представитель количества, но сами эти операции не могут быть приложены к реальным объектам, и поэтому числа и объекты с точки зрения этой деятельности оказываются отнюдь не тождественными. Одним из следствий этого вывода должно быть различение двух типов деятельности: 1) «объектной» и 2) «необъектной», или собственно «знаковой». Именно на основе этого различения типов деятельности должно производиться одно из различений возможных заместителей объектов, или, если принять иную терминологию, знаков. Замещение объектов знаками может осуществляться как в связи с одной, так и в связи с другой деятельностью, но характер знаков в этих случаях будет различным: при объектной деятельности заместители должны быть тождественны объектам в отношении выделяемого свойства, при необъектной деятельности этого тождества не требуется. Первый вид заместителей в контексте этого различения мы будем называть «знаками-моделями», второй вид — «знаками-символами». В более общем виде этот же вывод может быть сформулирован так: одно и то же объективное содержание может быть выражено в различных знаках — в зависимости от того, какую задачу решает это выражение и в какую систему действий оно в связи с этим включено. Когда знаки выступают в качестве моделей, то они чаще всего включены в объектную деятельность; но они могут быть и символами, и тогда это значит, что существует система особых, необъектных действий, которая и делает возможным замещение объектов совсем не похожими на них знаками — символами 12. После разбора этого примера, вводя ряд новых понятий, мы можем вернуться к вопросу о роли чертежей в «геометрическом» мышлении и выразить основную мысль, высказанную выше — что геометрические фигуры и чертежи в каком-то отношении сами являются объектами, — несколько иначе. Теперь мы скажем, что геометрические фигуры и чертежи в ряде случаев, то есть по отношению к целому ряду операций, являются знаками-моделями реальных тел и объективных пространственных отношений между ними. Но эта функция — не единственная из тех, в которых выступают фигуры или чертежи в системе науки геометрии, и не основная. Можно, конечно, предположить, к примеру, такую систему отражения действительности, в которой чертежи являются единственным видом знаков и к ним применяется только одна операция, устанавливающая их подобие. В такой системе отражения чертежи или фигуры были бы только знаками-моделями реальных объектов и ничем иным. Но в действительной науке геометрии чертежи отнюдь не являются единственными знаками. Рядом с ними мы видим знаки по крайней мере ещё двух видов:
А если в дополнение к этому мы возьмём также и приложения геометрии, то должны будем принять во внимание и ещё один вид знаков — арифметические. Указанное обстоятельство неимоверно усложняет всю картину и сразу же заставляет нас поставить принципиальный вопрос: можно ли рассматривать все эти четыре языка — чертежей, словесный, алгебраический, арифметический — как лежащие наряду друг с другом (а следовательно, как непосредственно относящиеся к реальным объектам и пространственным отношениям между ними) или, может быть, между этими языками существует своя иерархия отношений и одни из них относятся к объектам непосредственно, а другие через посредство первых? От ответа на этот вопрос зависит очень многое в нашем понимании природы «геометрического «мышления» и мышления вообще. Анализ рассуждений, содержащих решение конкретных задач с помощью методов элементарной геометрии, показывает, что это отношение может быть как одним, так и другим. Например, при получении целого ряда алгебраически выраженных соотношений, связывающих количественные характеристики элементов различных геометрических фигур, мы совсем не обращаемся к реальным телам и пространственным отношениям между ними; в этом случае в качестве объектов рассмотрения перед нами выступают исключительно одни геометрические фигуры. Здесь, следовательно, мы имеем отношение второго типа. Когда же, используя геометрический чертёж и алгебраические соотношения, полученные на его основе, мы наряду с ними используем также числовые значения различных величин, полученные непосредственно из измерения каких-либо объектов или расстояний между ними, то сами эти алгебраические соотношения выступают в отнесении непосредственно к объектам. Здесь, следовательно, имеет место первое отношение: все языки как бы непосредственно относятся к самим физическим объектам. Другими словами, когда условия задачи содержат определённые числовые значения, то это есть способ непосредственного описания объектов, по отношению к которому чертежи, используемые в процессе решения задачи, суть не что иное, как побочные, вспомогательные модели, также непосредственно относящиеся к реальным объектам и, следовательно, лежащие как бы наряду с числовыми знаками. Благодаря наличию числовых знаков, алгебраические соотношения, полученные из анализа чертежей, приобретают относительную самостоятельность по отношению к последним, и их начинают относить к реальным объектам через посредство числовых значений, минуя чертежи. Анализ рассуждений в собственно науке геометрии, напротив, приводит к выводу, что там фигуры и чертежи являются единственными «истинными» объектами и что обычный словесный язык и язык алгебраических соотношений (языка арифметики там в принципе нет; такие числа, как p, образуют особый случай) относятся только к ним. Дело в том, что понятие знака фиксирует функциональное свойство, и поэтому геометрические чертежи (как, в принципе, и все другое) являются знаками лишь до тех пор, пока они находятся во взаимосвязи замещения или обозначения и рассматриваются, соответственно, как её элементы 13. Но такое отношение существует, фактически, только за пределами собственно науки геометрии, именно, при решении практических задач «с помощью геометрии». В самой науке геометрии нет никаких других объектов, кроме самих фигур. Но зато эти фигуры являются «истинными» объектами, то есть тем, что можно дальше анализировать и расчленять, подобно тому, как в разбиравшемся выше «арифметическом» примере «истинными» объектами по отношению к действию пересчёта могли стать зерна проса, и подобно тому, как в современной теоретической арифметике «истинным» объектом является натуральный ряд чисел. Иначе можно сказать, что в собственно геометрии чертежи как бы «противостоят» обычным словесным и алгебраическим знакам в качестве объектов как таковых. Сделанные выше выводы о том, что чертежи или фигуры в «геометрическом «мышлении» могут выступать по меньшей мере в двух различных функциях — как знаки-модели и как объекты, поднимают ещё целый ряд сложных и принципиальных вопросов.
Систематическое рассмотрение всех этих вопросов — дело специального исследования. Нам же сейчас важно сделать выводы в плане уточнения методов анализа эмпирически заданных текстов. Обосновывая тезис о том, что чертежи геометрии являются одновременно как знаками-моделями определённой действительности, так и объектами исследования, мы вместе с тем, фактически, пришли и к другому исключительно важному выводу: тексты такого типа, как разбираемый нами, содержат целый ряд различных и относительно замкнутых языков. Причём важно, что эти языки лежат не в одном ряду, а образуют как бы различные «слои» текста; элементы одного языка, например языка чертежей, могут выступать в роли объектов, описываемых с помощью других языков. Последующие выводы, к которым мы приходим продолжая этот анализ, таковы. 3.Процессы мышления, приводящие к образованию новых знаний в геометрии, обязательно имеют двухплоскостную структуру и захватывают по меньшей мере два языка; один выступает как образующий плоскость объектов, и в нём осуществляется своё, содержательное движение, а другой — как образующий плоскость знаковой формы, и в нём содержательные преобразования замещаются и фиксируются. 4.Плоскость знаковой формы сама неоднородна: она содержит, с одной стороны, описания преобразований в плоскости содержания, а с другой, — фрагменты чисто формальных систем, внутри которых движение идёт без обращения к содержанию, в соответствии с определёнными общими правилами. 13Правильность этих выводов может быть без труда подтверждена на эмпирическом материале. Уже самого поверхностного взгляда на употребляемые в геометрии предложения обычного словесного языка достаточно, чтобы заметить, что они бывают по меньшей мере двоякого типа. Одни составляют логические связи вида «А есть В» или «Если А, то В», имеющие самостоятельное значение и используемые в дальнейшем в качестве общих положений (сюда относятся формулировки теорем, а также некоторые из общих понятий и постулатов Евклида). Предложения другого типа — это описания действий с геометрическими фигурами, построений и их преобразований. Они не являются общими положениями и относятся к определённым единичным построениям или преобразованиям. Приведём в качестве примера доказательство предложения 32 первой книги «Начала Евклида» [Евклид 1948: 43–44]. «Во всяком треугольнике по продолжении одной из сторон внешний угол равен двум внутренним и противолежащим, и внутренние три угла треугольника вместе — равны двум прямым. Пусть треугольник будет АВС, продолжим одну его сторону ВС до D; я утверждаю, что внешний угол АСD равен двум внутренним и противолежащим САВ, АВС и что внутренние три угла треугольника АВС, ВСА, САВ «вместе равны» двум прямым.
Действительно, проведём через точку С прямую СЕ, параллельную АВ. И поскольку АВ параллельна СЕ и на них пала АС, то накрестлежащие угли ВАС, АСЕ равны между собой (предложение 29). Далее, поскольку АВ параллельна СЕ и на них пала прямая ВD, то внешний угол ЕСD равен внутреннему и противолежащему АВС (предложение 29). Но АCE по доказанному равен BАС; значит, весь угол АСD равен двум внутренним и противолежащим углам ВАС и АBС. Прибавим общий угол АСВ; значит, углы АСD и АСВ (аксиома 2) равны трём углам АВС, ВСА, САВ. Но ACD и АСВ равны двум прямым (предложение 13); и, значит, АСВ, СВА, САВ вместе равны двум прямым. Значит, во всяком треугольнике по продолжении одной из сторон внешний угол равен двум внутренним и противолежащим «вместе», и внутренние три угла треугольника «вместе» равны двум прямым; что и требовалось доказать». Курсивом мы выделили предложения первого типа и выводы из них. В квадратных скобках стоят повторения и замечания от автора, не имеющие прямого отношения к самому ходу рассуждения. Без всяких выделений остались предложения второго типа, описывающие процесс построения. Если теперь отбросить все выражения в квадратных скобках, то нетрудно заметить, что процесс доказательства теоремы в рассматриваемом случае распадается на две отчётливо обособленные друг от друга части: 1) построение, фиксируемое в словесных выражениях, и 2) выводы, основанные на использовании общих положений того или иного вида. Какую роль играет каждая из этих частей доказательства? Что представляют собой словесные выражения, составляющие их? Начнём с анализа построения. Уже при самом поверхностном подходе бросается в глаза, что используемые в ходе доказательства общие положения — «поскольку АВ параллельна СЕ», и так далее — относятся совсем не к той фигуре, которая задана исходными условиями теоремы, не к треугольнику с продолженной стороной, и, следовательно, чтобы применить их в данном рассуждении, необходимо предварительно превратить эту заданную фигуру в ту, к которой относятся эти положения, или, во всяком случае, При этом для содержания самого процесса мышления часто неважно, как именно мы осуществляем само это преобразование: реально вычерчивая сами фигуры и вспомогательные линии или проделывая это в представлении и словесном описании — при достаточном опыте в первом, второе не так уж трудно. Для содержания процесса мышления, повторяем, важно только, чтобы это преобразование было обязательно осуществлено. Перейдём теперь к разбору второй части доказательства общих положений и выводов из них. Уже первый подход к этой части показывает, что и она, в свою очередь, не является однородной, а содержит по крайней мере две различающиеся между собой группы языково-мыслительных структур. К одной должны быть отнесены выражения «поскольку АВ параллельна СЕ и на них пала АС, то накрестлежащие углы ВАС, АСЕ равны между собой» и «поскольку АВ параллельна СЕ и на них пала прямая ВD, то внешний угол ЕCD равен внутреннему и противолежащему АВС» со ссылками на предложение 29, а также выражение «но АСD и АСВ равны двум прямым» со ссылкой на предложение 13. (Мы выделили эти выражения курсивом.) К другой группе должны быть отнесены выражения «Но АСЕ по доказанному равен ВАС; значит, весь угол АСD равен двум внутренним и противолежащим углам ВАС и АВС», «прибавим общий угол АСВ; значит, углы АСD и AСB равны трём углам АВС, ВСА, САВ» со ссылкой на аксиому 2 и, наконец, выражение «(но АСД и АСВ равны двум прямым), и, значит, АСB, СВА, САВ «вместе равны» двум прямым». Все эти выражения, за исключением выражения, взятого в последнем случае в фигурные скобки, мы выделили полужирным курсивом. Выражение в фигурных скобках, зафиксированное словесно только один раз, фактически участвует в доказательстве два раза в различных группах структур; при «разметке» выражений нам удобней было отнести его к первой группе 15. За выражениями, отнесёнными нами к первой группе, скрываются совершенно одинаковые с логической точки зрения мыслительные процессы — это применение общего положения к единичным случаям (или, как мы их называем, процессы «соотнесения общего формального знания с единичными объектами»). Общие положения, используемые в этом процессе, имеют структуру вида «если А есть B, то С есть D» (или, что то же самое, «если А обладает свойством В, то С обладает свойством D»), а суть самого процесса состоит в том, что у определённых элементов объекта, удовлетворяющих признаку А, эмпирически обнаруживают свойство В, а затем, опираясь на логическую связь общего положения, приписывают другим определённым элементам этого единичного объекта, удовлетворяющим признаку С, свойство D. Уже по внешней языковой форме соответствующих мест доказательства, в том числе по языковой форме самих этих выражений, без труда можно убедиться, что два первых выражения рассматриваемой группы имеют именно такую логическую структуру: наличие у определённых элементов А объектов этих выражений свойства В (к примеру в первом из этих случаев — параллельность линий АВ и СD, пересекаемых линией ВD) определяется «операционально», построением («проведём через точку С прямую СЕ, параллельную АВ»), точно так же определяется наличие свойства С у других элементов (углы ВАС и АСЕ — накрестлежащие), а свойство D (равенство) им приписывается. Но и третье выражение, несмотря на свою кажущуюся особенность, фактически ничем не отличается от двух первых. Различие в языковой форме между ним и двумя первыми выражениями является чисто внешним и возникло за счёт сокращения речи. Если это сокращение устранить, то третье выражение примет, фактически, тот же самый характерный вид: «Поскольку СА — прямая, восставленная на прямой ВD, то образованные ей углы АСD и АСВ «вместе равны» двум прямым», — «скрывающий» эмпирическое операциональное выявление элементов и свойств A, B, C в заданном чертеже-объекте и приписывание его элементам C свойств D. Таким образом, суть мыслительных процессов, фиксируемых тремя выделенными выражениями, состоит в применении общего положения к единичным объектам и в приписывании этим единичным объектам свойств, которые были уже зафиксированы у соответствующего класса объектов. В эти процессы, как показал анализ, вопреки мнению представителей формалистического направления, входят в качестве необходимого элемента операциональные моменты, связанные с обращением к объектам-чертежам и с определёнными действиями по отношению к этим объектам — построением или предметно-чувственным сравнением. И до тех пор, пока мы не осуществим этих действий с объектами-чертежами, мы не можем применять к ним общих положений. Рассмотрим в дополнение к этому процессы, приводящие к самим этим общим положениям, к примеру доказательство предложения 29 (см. [Евклид 1950: 41–42]). Так же, как и в доказательстве предложения 32, в нём можно выделить две части:
Но доказательства предложений 15 и 13, в свою очередь, содержат определённые преобразования заданных фигур и их элементов (там же, с. 28–29, 26–27). Таким образом, получается, что и та часть доказательства предложения 32, которая выражается непосредственно общим положением, в неявном, скрытом виде содержит определённые, производимые на чертежах преобразования и сопоставления. Таким образом, выясняется, что доказательство теоремы в геометрии Евклида обязательно содержит в себе специфические действия с чертежами — и не только в той части, в которой эти действия явны, но и в той, которая, казалось бы, свободна от них и состоит исключительно из готовых словесных формулировок. Такой вывод тотчас же поднимает «обратные» вопросы: а какую роль тогда играют эти словесные выражения? зачем они нужны? почему прибегают к их помощи? и так далее. Но прежде чем попробовать ответить на них, рассмотрим другую группу словесных выражений второй части доказательства. На первый взгляд, представляется (особенно для человека, который современные способы и формы мышления воспринимает как единственно возможные и всегда существовавшие), что это чисто формальное преобразование величин, осуществляемое в соответствии с правилами алгебры (или теоретической арифметики) и что если представить их в строгой алгебраической форме, то это станет очевидным. Попробуем это сделать со всей возможной полнотой и строгостью. Первое словесное выражение примет вид:
Второе выражение примет вид:
А третье, соответственно, примет вид:
Если в первом выражении рассматривать (1), (2), (3) как одно преобразование, а (3), (4) и (5) как другое 16, и при этом предположить, что исходные предложения каждого из этих преобразований в отдельности заданы и рассмотрение способа получения их не входит в задачу исследования, то, действительно, можно будет согласиться с тем, что эта часть доказательства носит формальный характер и подчиняется соответствующим алгебраическим (или теоретико-арифметическим) аксиомам. Однако, чтобы этот вывод имел какое-либо значение, необходимо одновременно выяснить: 1) носили ли они у Евклида такой характер, какой получили при алгебраическом представлении, и 2) можно ли в контексте решаемой нами задачи рассматривать эти преобразования по отдельности, безотносительно к общей линии доказательства? Обращаясь к Евклиду, нетрудно заметить, что для него эти преобразования не имели одинакового смысла и значения. Начать хотя бы с того, что второе выражение начинается с особой фразы «прибавим общий угол АСВ…» и содержит ссылку на аксиому (или общее понятие) 2, а первое выражение, хотя, казалось бы, скрывающийся за ним процесс мысли тоже состоит в прибавлении равных количеств к равным, не содержит такой фразы и такой ссылки на аксиому, хотя как первое по порядку именно оно должно было бы их содержать. Это различие можно объяснить только в том случае, если мы будем рассматривать эти словесные выражения одновременно с чертежами и, в частности, учтём особую роль исходного чертежа, который со всеми своими элементами и сторонами выступает как исходный объект, подлежащий исследованию как актуально существующий независимо от деятельности исследователя и в этом отношении существенно отличается от всего того, что исследователь создаёт в дальнейшем в ходе геометрических преобразований. При таком подходе представляется вполне естественным, что Евклид в первом случае не говорит о прибавлении углов АСЕ и ЕСD друг к кругу, так как оба они вместе суть с самого начала один угол АСD, заданный исходным чертежом, а во втором говорит о таком прибавлении, так как ðАСD и ðАСВ на исходном чертеже — разные углы. Между прочим, только такой подход к анализу этой части доказательства даёт возможность понять происхождение соотношения (4) в алгебраическом представлении первого выражения. В то время как все другие исходные соотношения приведённых выше преобразований логически выводятся на основе других рассуждений и поэтому при раздельном рассмотрении этих преобразований без особой ошибки могут рассматриваться как заданные, соотношение (4) разрушает такой подход. При алгебраическом представлении этой части доказательства мы должны либо рассматривать его как определение ðACD, что противоречит смыслу всего анализируемого рассуждения, либо искать ему особое основание. Но никакого логически-формального основания для него нет, и поэтому нам остаётся только одно — обращение к чертежу и ссылка на операциональный ( 14Другим доказательством того, что рассматриваемые словесные выражения у Евклида тесным образом связаны о чертежами и, в частности, с действиями по отношению к этим чертежам, служит то обстоятельство, что аксиомы (или общие понятия) первой книги «Начал» (на одну из которых имеется ссылка в рассматриваемом рассуждении) имеют своим предметом не числа и не алгебраические величины, а геометрические объекты — линии, углы, площади, и так далее. В этом отношении исключительно характерна аксиома 7: «И совмещающиеся друг с другом равны между собой». Фактически, она представляет собой операциональное определение абстракции «равно» (и соответственно «не равно») при оперировании геометрическими чертежами и только по отношению к ним имеет смысл. «Равенство Евклид всегда понимает в смысле равновеликости, — пишет Д. Д. Мордухай-Болтовский. — … Евклид хотел сказать …, что площади двух совпадающих при наложении фигур равны» [Мордухай-Болтовский 1948: 250–251] 17. Уже одна эта характеристика аксиомы 7 достаточно подтверждает выдвинутое нами положение. Но не в меньшей степени его подтверждают и другие аксиомы: «
Многие комментаторы нового времени считают их родоначальницами системы арифметических аксиом. Так характеризует их, в частности, и Д. Д. Мордухай-Болтовский (там же, с. 247). С нашей точки зрения, не может быть большей исторической ошибки. Дело в том, что все эти аксиомы в равной мере бессмысленны как по отношению к числам, так и по отношению к величинам. Между прочим, и в комментариях у Мордухай-Болтовского одной страницей дальше, после того как он характеризует эти аксиомы как родоначальницы арифметических аксиом, следует место, которое полностью опровергает какую-либо возможность такой их трактовки. Он пишет: «В системе Гилберта первая евклидова аксиома исчезла как арифметическая, но остаётся как геометрическая аксиома группы конгруэнтности, если AB ºº A¢B¢ AB ººA²B² то A¢B¢ ººA²B² Равенство чисел есть тождество чисел, и поэтому аксиома 1 в числах ничего не выражает (курсив мой. — Прим. авт.). То же следует сказать и о второй евклидовой аксиоме; она не выражает больше, чем аксиома первого сочетания. Пятая отпала как следствие второй, а шестая заменилась более общей, которая в системе Гилберта сводится к пятой. Таким образом только четвёртая осталась в современной системе 19. Законов счета Евклид не рассматривал» (там же, стр. 248). Принципиально такую же характеристику в отношении применимости аксиом Две величины не могут быть равными, но лишь тождественными (это положение вполне отвечает аналогичному положению в арифметике о том, что нет равных чисел, а есть одно и то же число, воплощённое в различные собрания). Следовательно, две различные величины необходимо не равны; и это отношение неравенства служит для характеристики величин одного и того же рода: две величины — одного и того же рода, когда про одну из них можно сказать, что она больше или меньше другой» [Кутюра 1913: 88–90]. И затем Кутюра формулирует пять аксиом [Кутюра 1913: 90], необходимых для построения теории величин. Четыре из них характеризуют взаимоотношения внутри формы теории:
По поводу последней аксиомы — этот момент исключительно важен и будет использован нами в дальнейших выводах — Л. Кутюра пишет следующее: «Последнюю аксиому можно назвать принципом тождества неразличимых в применении к величинам … Иначе говоря, так как величины, конкретизированные в пространстве и времени, называются количествами, то одно и то же количество не может соответствовать двум различным величинам одного и того же рода; или ещё: отношение количества к соответственной величине однозначно; каждое количество одноимённо определяет соответственную величину, что вполне понятно, ибо величина извлечена из количества путём абстракции» (там же, с. 90–91). Мы оставляем сейчас в стороне разбор всего приведённого фрагмента из книги Кутюра и анализ его логического смысла и значения и хотим подчеркнуть только один момент: в нём убедительно показано, что аксиомы 1–6, которыми пользовался Евклид, не могут относиться к величинам (а также и к числам). Но Евклид пользовался ими и, следовательно, предметом его «Начал» являются не числа и не величины, а нечто другое. Этим другим, по выражению Кутюра, — и здесь мы должны обратить особое внимание на первую и последнюю часть приведённого фрагмента — должны быть величины, конкретизированные в пространстве и времени, количества, сами предметы, которым мы приписываем эти величины. А в геометрии Евклида такими конкретными количествами или предметами (точнее, объектами) могут быть только геометрические фигуры или чертежи. Таким образом, по всем перечисленным выше признакам три выделенных нами, казалось бы, чисто словесных и формальных выражения, на самом деле у Евклида тесным образом связаны с чертежами и являются фактически лишь описаниями, сопровождающими геометрические преобразования чертежей. Именно такой смысл и значение имеет фраза в начале второго выражения: «прибавим общий угол АСВ»; она описывает действие, которое должно быть произведено, хотя и в подразумеваемом плане, но именно с углом и именно геометрическим, «чертежным» способом. А в первом выражении нет такой фразы, потому что углы АСЕ и ЕСD не нужно прибавлять друг к другу, так как они с самого начала составляли один угол АСD и получились в результате «условного», если можно так сказать, разбиения его на части линией ЕС. Но последнее замечание совершенно И ставя так вопрос, мы переходим, фактически, к обсуждению того самого вопроса, который вторым был сформулирован выше: можно ли рассматривать выделенную группу словесных преобразований саму по себе, безотносительно к общей линии и структуре всего доказательства? Ведь если на первый вопрос мы ответим утвердительно: да, выделенные действия разбиения заданного угла на части и объединения этих частей в одно целое надо рассматривать как органически связанные элементы одного процесса мышления, ибо при разбиении уже заранее имелось в виду, предполагалось такое и именно такое объединение, — то это будет означать вместе с тем, что мы отрицательно отвечаем на второй, более общий вопрос: словесную часть доказательства теоремы в «Началах» Евклида вне чертежей и действий с ними нельзя рассматривать не только как целостное, самостоятельно осуществляемое доказательство, но даже как относительно самостоятельную часть целостного доказательства. К этому выводу примыкает, далее, ещё одно соображение. Поставим вопрос: какие элементы рассуждения в доказательстве дают нам возможность получить новые положения, новые знания? Та часть доказательства, которая содержит ссылки на другие предложения, как мы уже выяснили, является применением уже готовых, выработанных общих положений к единичным случаям. Сами по себе эти процессы мысли не дают ничего нового для системы геометрического знания. Новое, как мы уже видели из предшествующего анализа, получается за счёт построений, связанных с этими процессами мысли, за счёт преобразований исходных геометрических объектов к новому виду. Но и другая часть словесного рассуждения в доказательстве, взятая сама по себе, как мы только что выяснили, тоже не содержит ничего нового, так как является лишь «обратным процессом возвращения» к исходному объекту. И здесь точно так же новое возникает, фактически, только благодаря построениям, производящим исходное расчленение. Если к этому добавить, что и каждое из общих предложений, применяемых в ходе доказательства, имеет за собой определённые геометрические построения, то мы придём к выводу, что для того, чтобы раскрыть действительное ядро и сердцевину процессов, приводящих к этим общим предложениям, необходимо проанализировать ту последовательность собственно геометрических, «чертежных» преобразований и сопоставлений, которая скрывается за всем рядом этих предложений 20. Эти соображения также подтверждают тот общий вывод, что словесную часть доказательства теоремы в «Началах» Евклида нельзя отделять от чертежей и действий с ними. 15Выводы, полученные в предшествующем пункте, по видимости вступают в противоречие со взглядами подавляющего большинства современных геометров — представителей так называемого «формалистического» понимания, которые считают, что чертежи являются совершенно излишними в геометрическом доказательстве, которое может быть проведено сугубо формально. Вот что пишет, к примеру, Л. Кутюра: «Если бы даже построения были безусловно необходимы, они не заключали бы в себе обращения к наглядному представлению. Но они далеко не так необходимы, как это думают на основании «элементов» синтетической геометрии. Искусственный характер доказательств Евклида уже давно подвергался резкой критике, так как эти доказательства опираются на построения, подчас сложные и, Своё понимание Кутюра иллюстрирует примером доказательства, заимствованного из элементарного учебника, который, по его выражению, «не проникнут духом какой-либо системы» и «преследует единственно логическую строгость, наряду с педагогическим порядком и ясностью». Вот это доказательство: «Если две плоскости взаимно-перпендикулярны, то всякая прямая, лежащая в одной из них и перпендикулярная к линии их пересечения, перпендикулярна к другой. Ибо эту прямую можно рассматривать как линию пересечения первой плоскости с третьей, перпендикулярной к линии пересечения данных (95) и, следовательно, перпендикулярной ко второй [107, 111] [Кутюра 1913: 241]». «Это доказательство, состоящее из одной фразы, не обращается к помощи каких-либо фактов наглядного представления: оно не сопровождается никакой геометрической фигурой и, как мы видим, не требует никакого построения, — пишет Кутюра. — Оно просто ссылается на три предыдущих предложения и ограничивается сопоставлением и сочетанием их. Чтобы его понять, надо знать эти предложения: (95) Через точку плоскости, заключающей прямую, можно провести к этой прямой только один перпендикуляр; и этот перпендикуляр есть линия пересечения данной плоскости и плоскости, перпендикулярной к данной прямой и проходящей через данную точку. (107) Две плоскости взаимно перпендикулярны, когда одна из них содержит прямую, перпендикулярную к другой. (111) Если две пересекающихся плоскости перпендикулярны к одной и той же третьей плоскости, то к ней перпендикулярна и линия их пересечения» [Кутюра 1913: 241]. Затем Л. Кутюра анализирует ход самого доказательства: «Условие теоремы содержит в себе: две взаимно-перпендикулярных плоскости, назовём их P и Q, линию их пересечения, назовём её D, и прямую Е, перпендикулярную к D в Р. Прямая E (в силу (95) есть линия пересечения плоскости Р плоскостью R, перпендикулярной к прямой D. Но (в силу (107) плоскость R, перпендикулярная к прямой D плоскости Q, перпендикулярна к Q. Обе плоскости Р и R перпендикулярны к Q, значит (в силу (111) линия их пересечения Е перпендикулярна к Q, что и требовалось доказать» (там же). И далее идут исключительно характерные положения: «Мы намеренно не делаем чертежа, ибо он совершенно бесполезен. Нет необходимости видеть плоскости P, Q, R и прямые D, Е; достаточно знать, каковы их взаимные отношения и применить к ним, так сказать автоматически, три предложения: (95), (107) и (111). Это — словесное, то есть формальное доказательство. Можно было бы отнять всякое геометрическое значение у сущностей D, E, P, Q, R, равно как у связывающих их отношений перпендикулярности и принадлежности — рассуждение осталось бы тем же и имело бы ту же силу, раз предполагаются верными три предложения (95), (107), (111). Этот пример показывает, что геометрическое доказательство может (и должно) быть чисто логической дедукцией. Следует прибавить, что рассмотренная нами теорема отнюдь не является корроларием (то есть непосредственным следствием из другой) и что цитированное доказательство не представляет в названной к книге исключения: в ней большая часть доказательств имеет тот же характер, причём в них так же мало, как и в рассмотренном случае, прибегают к геометрическим изображениям, к построениям» (там же, с. 241–242). Как же надо относиться ко всем этим рассуждениям Л. Кутюра и аналогичным рассуждениям других представителей «формалистического» направления? Правильно или неправильно оценивается в них характер доказательства в разобранном примере, а вместе с тем и во всей современной геометрии? И если эта оценка правильная, то может ли она служить опровержением сформулированного нами выше вывода относительно характера доказательства в «Началах» Евклида? Все эти вопросы суть лишь формулировки различных частных аспектов одного более общего вопроса, который мы уже ставили выше: какую роль играют словесно-алгебраические выражения в системе геометрии, как они относятся к преобразованиям чертежей? И чтобы ответить на него, хотя бы в общем виде, надо встать на историческую точку зрения и рассмотреть условия и закономерности формирования формального умозаключения вообще и формального умозаключения в геометрии, в частности. Начнём с анализа условий формирования любого формального умозаключения. Всякое знание, каким бы опосредствованным по отношению к объекту оно ни было, возникает первоначально как констатация определённого эмпирически выявленного положения дел (в предметной области или в области знаков). Иначе говоря, исходным для каждого типа знаний является описание. Умозаключение вырастает из описания определённого типа. Первоначально та последовательность утверждений, которую мы теперь рассматриваем как силлогистическое или какое-либо иное умозаключение, появляется как случайное (для субъекта) совпадение эмпирически констатированных утверждений. Например, если даны три предмета — А, В и С, то три последовательных сопоставления их между собой дают три эмпирических утверждения вида «А B», «В> С», «А С». Или если даны n предметов, то три ряда последовательных сопоставлений (например, атрибутивных и согласования) могут дать три эмпирических утверждения, значимых для этой предметной области, вида: «Все А обладают свойством В», «Все В обладают свойством С», «Все А обладают свойством С». Но многократное сопоставление таких троек утверждений, различающихся по своему предметному содержанию, позволяет вывести (так же эмпирически, то есть опираясь на анализ существующих утверждений) правило вида: «Если утверждается, что А В и B C, то можно утверждать, что А> C», или аналогичное ему правило: «Если утверждается, что все А обладают свойством В и все b обладают свойством С, то можно утверждать, что все a обладают свойством C». Лишь после стихийного выделения (а затем и сознательного формулирования) такого правила впервые становится возможным формальное, или дедуктивное (в традиционном смысле), умозаключение (или вывод) вида: «А есть В, В есть С, следовательно, А есть С». Его заключение «А есть С» получается не на основе констатации, не на основе выявления определённого положения дел в эмпирической действительности, а помимо него — в силу правила. Оно апеллирует не к положению дел, а к общей значимости правила; оно говорит не о том, что есть, а о том, что должно быть. Собственно, поэтому оно и называется формальным. Если изображать движение мысли в этих двух случаях схематически, то это будет выглядеть примерно так:
(Нижняя строчка изображает здесь плоскость содержания, а верхняя — плоскость знаковой формы.)
(Нижняя строчка изображает плоскость содержания, вторая снизу — знаковую форму эмпирически полученных утверждений, третья — формальное преобразование эмпирически полученной знаковой формы, а четвёртая — правило, в соответствии с которым это преобразование производится.) Таким образом, всякое умозаключение связано, во первых, с потерей на определённом отрезке непосредственной отнесённости к плоскости содержания, во-вторых, с появлением новой плоскости — правила, в соответствии с которым совершается умозаключение. После этих предварительных замечаний относительно условий появления и строения всякого умозаключения мы можем перейти к анализу специфических особенностей умозаключения в геометрии. В истоках геометрии, по признанию многих, лежит деятельность измерения. В основе самой операции измерения лежит другое действие — наложение. Поэтому мы должны начать с анализа именно этого действия. Наложение двух объектов друг на друга очень часто осуществляется в процессах труда, когда нужно создать объект — орудие или предмет потребления, — по форме тождественный другому объекту. Первый объект в этой ситуации выступает как предмет труда, второй — как эталон. Такое наложение друг на друга предметов труда и эталонов по сути своей всегда есть приравнивание, или отождествление: если исходный объект — предмет труда — не равен эталону, то первоначально его просто изменяют практически, преобразуют, добиваясь такого равенства; собственно в этом и состоит задача трудового акта. Но затем, в определённых трудовых ситуациях такое наложение объектов друг на друга начинает играть иную роль; оно становится познавательным действием, а его задачей и целью — получение знания вида: предмет труда «равен» (или «не равен») эталону. При этом важно отметить — и это понадобится нам для дальнейшего, — что факт совмещения или несовмещения объектов при наложении, независимо от того, является это действие практическим или познавательным, устанавливается с помощью зрительного, визуального наблюдения. Осуществляя наложение в предметном плане и фиксируя зрительно, совместились или не совместились накладываемые друг на друга объекты, человек тем самым выделяет (обнаруживает) в объективной действительности новое содержание. Это содержание фиксируется в слове «равно» (или «не равно»). Наглядно-символически эту операцию, то есть действие наложения и устанавливаемую на его основе связь между словом и объектами, можно изобразить в схеме:
Где А и В — накладываемые друг на друга объекты, фигурная скобка обозначает отношение наложения, а (a) — слово, фиксирующее новое содержание, выделенное посредством наложения, — равенство или неравенство объектов А и В. Такова (в первом приближении) структура одной из операций, лежащих в основе элементарной геометрии. Нам важно здесь подчеркнуть её «двухплоскостной» характер: объекты А и В, накладываемые друг на друга, лежат в одной, «нижней», плоскости, а слово (a) — в другой, «верхней», плоскости; элемент верхней плоскости фиксирует, обозначает, отражает то свойство (в широком смысле этого слова), которое обнаруживается в результате определённого действия с элементами «нижней» плоскости. Можно сказать, что элемент (a) «верхней» плоскости служит заместителем содержания, выделенного посредством действия с объектами «нижней» плоскости. Таково исходное отношение между словесными выражениями, объектами-чертежами и действиями с ними для геометрии. Но это отношение — лишь исходное. В самой геометрии оно носит существенно иной и значительно более многообразный характер. Возьмём то же действие наложения. В мире объектов мы производим наложение практически; в мире же чертежей геометрии действовать таким образом невозможно — уже хотя бы потому, что чертежи существуют на песке или на листе бумаги. Следовательно, наложение приходится осуществлять в представлении, в «воображаемом» или «подразумеваемом» плане. Но как в таком случае выяснить результат? При подразумеваемом наложении он теряет всю свою определённость: фигуры могут оказаться как равными, так и неравными, и это невозможно выяснить с достаточной степенью точности. Но это означает, что в подразумеваемом плане действие наложения теряет свои смысл и значение в системе человеческой деятельности. Складывается весьма характерное положение: нужно установить равенство или неравенство фигур; единственным способом решения этой задачи является непосредственное наложение фигур друг на друга; но геометрические фигуры в силу особенностей их «материала» нельзя накладывать друг на друга непосредственно; их можно накладывать только в подразумеваемом плане, но такое наложение не решает задачи. Таким образом, возникает разрыв между способом существования объектов и деятельностью, которая может решить возникшую задачу. Этот разрыв должен быть преодолён за счёт появления новой деятельности, «подходящей» к способу существования объектов. Человеку приходится искать обходный путь для решения стоящей задачи. Сделаем «скачок»: оставим в стороне условия реального развития и попробуем решить вопрос, каким может быть этот «обходный путь» в условиях подразумеваемого плана. Здесь нам придётся прежде всего согласиться с тем, что ни один собственно объектный способ деятельности не может быть перенесён в подразумеваемый план так, чтобы он в то же время сохранил свою «продуктивность», то есть давал бы решение исходной задачи. Следовательно, обходный путь должен строиться на переходе к другому, необъектному способу деятельности. Но это может означать только одно: это должна быть деятельность со знаками и в плоскости знаков. В то же время эта деятельность должна быть такой, чтобы посредством неё мы имели бы возможность «выявлять» и «приписывать» объекту то свойство (в разбираемом случае это должно быть равенство или неравенство), которое мы до этого выявляли с помощью объектной операции. Но в плоскости знаков такой деятельностью могут быть лишь формальные переходы по готовым связям знаний 21. Наглядно-символически их можно изобразить в схеме: (b) → (a) ¯ (23) А… В где А и В — объекты; три точки означают, что в силу определённых особенностей объектов А и В наложение не может быть осуществлено; (a) — выражение, фиксирующее равенство (или неравенство) объектов А и В ; горизонтальная стрелка показывает, что это выражение формально выводится из Возникает вопрос: что представляют собой свойство b и связь между (b) и (a), позволяющая формально выводить второе из первого; откуда берутся это (b) и эта связь? Здесь, ещё до начала детального анализа можно с очевидностью утверждать следующее: как выражение (b), так и связь между (a) и (b) относятся к объектам А и В и были получены раньше, первое — как выражение Наглядно-символически в схеме это можно выразить так:
Где V-образный знак изображает то действие с объектами А и В, посредством которого выявляется как особое содержание связь (b) → (a), знак неизвестного пока сопоставления, состоящий из сплошной и штриховой линий, изображает действие, посредством которого в этих объектах выявляется свойство b, вертикальная линия — отношение отнесения знаковых выражений к объектам, вертикальная стрелка — приписывание свойства a объектам А и В, а две вертикальных линии êç — отношение «необходимой» связи знания (b) → (a) к определённому содержанию, полученному посредством неизвестной пока деятельности с объектами А и В (возможно, что в эту деятельность включены и другие объекты). Но это, в частности, означает, что с помощью одной лишь формальной деятельности со знаками ни одна объектная задача не может быть решена. Во-первых, само «формальное движение» предполагает в качестве своего обязательного условия наличие «необходимой» связи (b) → (a), а последняя сама могла быть получена только путём определённой объектной деятельности, вычисляющей саму связь между a и b как особое содержание; во-вторых, условием применения связи (b) → (a) к определённым объектам является обнаружение в них свойства b, а это обнаружение точно так же является определённой объектной операцией. Отсюда, в свою очередь, вытекает, что положение, сформулированное нами выше относительно средств обходного пути решения задачи, является по крайней мере неполным. Уточняя его, мы должны сказать, что обходный путь решения задачи строится на основе перехода, во-первых, к другим видам объектной деятельности, посредством которых устанавливается необходимая связь знания вида (b) → (a) и в заданных объектах обнаруживается свойство (b), во-вторых, также к формальным действиям перехода по готовым связям от (b) к (a), позволяющим приписать объектам непосредственно не обнаруженное в них свойство a. После этих замечаний мы можем поставить вопросы более конкретно: что представляет собой свойство b? в каком отношении оно стоит к свойству a? что представляет собой объектная операция, посредством которой свойство b выявляется и фиксируется, и, в частности, может ли она быть осуществлена в подразумеваемом плане? Чтобы наметить в общих чертах путь решения этих вопросов, рассмотрим более детально само действие наложения друг на друга объектов, к примеру, треугольной формы. Чтобы выяснить, совместились или не совместились эти объекты при наложении, мы смотрим сначала на одну пару их сторон и проверяем, совместились ли они, затем переходим к другой паре сторон и проверяем её, в заключение проверяем третью пару. Таким образом, уже при обычном практическом действии наложения проверка совмещения (а вместе с тем и само действие наложения) распадается на ряд частных действий, каждое из которых имеет своим предметом не объект в целом, а отдельные его стороны; вместе с тем и сам объект (с точки зрения этой серии действий) выступает уже не как тело или поверхность, а как фигура, составленная из одних линий-сторон. (В этом, между прочим, заложено основание для перехода от объектов к их моделям-чертежам.) Предположим теперь, что первая пара сторон наших объектов при наложении совместилась, а вторая — нет. Перед человеком, осуществляющим наложение, естественно возникает вопрос: в чём причина этого? От чего зависит или чем определяется то, что вторая пара сторон (при равенстве первой пары сторон) не совместилась? Фактически это означает, что перед человеком возникает задача выявить в объектах и сделать предметом специального рассмотрения Так или примерно так, путём анализа предметно-практического действия наложения и тех действий, которые производят, проверяя, произошло ли совмещение объектов (особенно благодаря анализу тех случаев, когда совмещения нет), приходят к выделению тех свойств, на основании которых, не производя самого наложения, можно судить, произойдёт ли совмещение объектов как целых 22. Мы оставим сейчас в стороне все вопросы о том, как именно фиксируются вновь выделенные «стороны» 23 — свойства объектов, как обнаруживается и фиксируется в специальных знаках их равенство, как устанавливается необходимый характер связи содержаний этих знаков с прежним признаком равенства объектов в целом, как находится знаковая форма для выражения этой связи и все подобные им (дать обоснованный ответ на все эти вопросы — дело систематического генетического исследования). В данной связи нам важно дать лишь самую общую схему обходного пути решения задачи и на её основе постараться дать ответ на поставленные выше вопросы, во-первых, относительно характера свойства b, его отношения к свойству a, природы операции, посредством которой выявляется b, и возможности осуществления её в подразумеваемом плане, во-вторых, относительно природы словесных рассуждений, входящих в систему геометрии. Для этого нам важно подчеркнуть следующее. Как показал разобранный пример, действие наложения двух объектов друг на друга — казалось бы одноактное и простое — распадается на ряд следующих друг за другом действий, каждое из которых выявляет особое содержание, фиксируемое в специальном словесном знаке. При этом происходит «анализ» исходных объектов А и В и выделяются определённые их «стороны» a1 и b1, a2 и b2, a3 и b3 (в данном примере — стороны объектов и углы между этими сторонами). Между знаками, фиксирующими равенство соответствующих «сторон» a1 и b1, a2 и b2, a3 и b3 — обозначим их как (b1), (b2), (b3), — и знаком a, фиксирующим равенство объектов А и В в целом, устанавливается каким-то образом связь (b1, b2, b3) → (a). После того, как эта связь установлена и закреплена, мы можем решать исходную задачу определения равенства исходных объектов А и В обходным путем: по отдельности устанавливая равенство «сторон» a1 и b1, a2 и b2, a3 и b3, а затем формально двигаясь по связи (b1, b2, b3) (a). При определённых условиях, когда в силу
Где a1 и b1, a2 и b2, a3 и b3 — «стороны» объектов А и В, сопоставляемые друг с другом через сопоставление их с эталонами Э1, Э2, Э3 (в частном случае это может быть один и тот же эталон), вертикально расположенные фигурные скобки изображают сами эти объектно осуществляемые сопоставления с эталонами, горизонтальные линии, попарно связывающие фигурные скобки, изображают сопоставления результатов первых сопоставлений, вертикальные линии, как обычно, связи со знаками, (b1), (b2), (b3) — знаки, фиксирующие содержание, выявленное посредством этих сложных сопоставлений, наклонная линия обозначает объединение свойств, фиксируемых этими знаками, в одно, (a) — знак, фиксирующий равенство объектов А и В как таковых, горизонтальная стрелка обозначает необходимую связь между (b1, b2, b3) и (a), а вертикальная стрелка вниз от (a) — приписывание соответствующей характеристики исходным объектам А и В. Но весь этот обходный путь решения задачи, изображённый на схеме, относится к тому случаю, когда мы имеем дело с объектами и устанавливаем равенство их «сторон» путём фактического наложения этих «сторон» друг на друга или эталонов на эти «стороны». Когда же мы переходим в сферу геометрии, где объектами оперирования являются чертежи-знаки, замещающие реальные объекты, тогда (по соображениям, которые мы уже излагали выше) фактическое, реально осуществляемое наложение становится невозможным: его надо осуществлять в представлении, подразумеваемым образом. Но при таком способе осуществления наложения становится неопределённым его результат. Следовательно, в собственно геометрии нельзя определять характеристики b1, b2, b3, а приходится предполагать, что они уже определены, то есть полагать действия наложения уже произведёнными, а содержание выявленным, причём, выявленным именно таким, какое требуется связью (b1, b2, b3) → (a). Но это означает, что равенство элементов a1 и b1, a2 и b2, a3 и b3 становится условием движения в собственно геометрии. Таким образом, в общих чертах мы отвечаем на вопрос относительно взаимоотношения свойств b и a и характера операции, вычленяющей b. Свойства b (так как их всегда оказывается несколько) представляют собой свойства, обязательно или «необходимо» обнаруживающиеся в отношениях между «сторонами», накладываемых друг на друга объектов, тогда, когда имеется налицо свойство a, характеризующее отношение между объектами в целом. В то же время свойства b являются такими, что наличие их обусловливает и наличие свойства a. Операции, посредством которых выявляются свойства a, насколько показывает разобранный пример, не могут быть осуществлены в подразумеваемом плане; поэтому они не могут осуществляться в собственно геометрии, и их результат предполагается уже данным. Но отсюда непосредственно вытекает другое важное следствие, характеризующее собственно геометрию и являющееся частью ответа на поставленный выше вопрос относительно природы словесных рассуждений, входящих в систему геометрии. Действительно, если знания (b1), (b2), (b3), фиксирующие равенство определённых элементов чертежа (эти элементы на языке геометрии выражают определённые «стороны» объектов), становятся условием движения в собственно геометрии и предполагаются уже данными, то само это геометрическое движение сводится лишь к фиксации в представлении последовательности осуществления подразумеваемых действий, или, иначе, последовательности привлечения в рассуждении знаний (b1), (b2), (b3). Но если таких действий длинный ряд, то фиксировать его в чисто предметном представлении просто невозможно; к этому добавляется необходимость сообщать об этой последовательности подразумеваемых действий другим; таким образом возникает словесное описание. Этот вывод, хотя он и сделан на основе очень грубого анализа, исключительно важен. Он позволяет объяснить появление в геометрии словесных описаний действий, осуществляемых в подразумеваемом плане, и показывает необходимость их появления. Остаётся не совсем выясненным вопрос о роли и значении для геометрии другого вида словесных выражений, именно, выражений вида (b) → (a), а вместе с тем не получен ещё ответ на вопрос о правомерности точки зрения Л. Кутюра и других представителей формалистического направления. Чтобы осветить эту сторону дела, необходимо вернуться к анализу обходного пути решения задач. Выше мы уже сказали, что новые объектные действия, к которым переходят от прежних при формировании какого-либо обходного пути решения задачи, должны соответствовать способу существования объектов. Если этого нет и объектная деятельность, необходимая для обнаружения свойств группы b, точно так же «не подходит» к способу существования объектов А и В, как и деятельность, приводящая к a, то уже разобранная схема обходного пути может быть применена вновь столько раз, сколько это необходимо, пока не будет достигнут переход к «подходящей» объектной деятельности. В схеме это выразится примерно так:
Где А и В исходные объекты, знак, состоящий из сплошной и штриховой линий, изображает сложную систему действий, посредством которой выявляются определённые характеристики отношений между «сторонами» объектов А и В (или в геометрии — элементами соответствующих этим объектам чертежей), (λ) — языковое выражение, фиксирующее эти характеристики, (a) — характеристика отношения объектов А и В, которую надо получить по условиям исходной задачи, (b)… (x) — «промежуточные» языковые выражения, позволяющие формально вывести (a) из (λ), горизонтальные стрелки обозначают «необходимые» связи между этими языковыми выражениями, V-образные знаки изображают сложные действия с объектами А, В и другими, посредством которых эти необходимые связи выявляются как особые содержания, вертикальные двойные штриховые линии обозначают связи между этими содержаниями и фиксирующими их языковыми формами вида (λ) → (x), наконец, вертикальная стрелка, идущая вниз от (a), обозначает «приписывание» формально выведенного свойства объектам А и В. Проанализируем некоторые аспекты содержания, выражаемого этой схемой. На основе всего разобранного выше можно утверждать, что какой бы длины ни были цепи формального выведения, они в своём конечном пункте предполагают в качестве обязательного условия определённую объектную деятельность. Это зафиксировано на схеме знаком сопоставления, приводящего к выражению (λ). Но, как и в более простых случаях, эта деятельность лежит за границами собственно геометрии: в последней просто предполагается, что эта деятельность уже осуществлена и нужный результат получен. Кроме того, обязательным условием появления самой этой цепи формального выведения является сложная система действий, с помощью которой выделяются и фиксируются как особое содержание сами связи между (λ), (x) … (b), (a). Поскольку в выделении этих связей и состоит специфическая задача геометрии, постольку действия, с помощью которых это выделение осуществляется, должны, очевидно, входить в её собственную систему. Выше, при разборе доказательств некоторых предложений из «Начал» Евклида мы показали, что эти действия представляют собой прежде всего преобразования чертежей, осуществляемые реально (например, с помощью циркуля и линейки) или в подразумеваемом плане (часто с помощью словесного описания). Фактически, они строятся по такой же схеме, как и любой другой процесс решения задачи: отдельные шаги в преобразовании чертежей фиксируются в связях знания, а последовательность и связь этих шагов определяют последовательность и связь структур знания. На схеме этот процесс будет выглядеть примерно так:
Где E, F, I, K — определённые объекты-чертежи, знак «ворот» éù изображает Нам в этой связи особенно важно подчеркнуть, что основание для перехода от (ψ) → (φ) к (μ) → (ν) и далее к (λ) → (χ) лежит в преобразовании чертежей. Если мы возьмём к примеру доказательство предложения 32 из «Начал» Евклида, то связь (λ) → (χ) будет изображать само это предложение («во всяком треугольнике по продолжении одной из сторон внешний угол равен двум внутренним и противоположным, и внутренние три угла треугольника «вместе» равны двум прямым» [Евклид 1948: 43]), связь (μ) → (ν) будет изображать предложение 29 («прямая, падающая на параллельные прямые, образует накрестлежащие углы, равные между собой, и внешний угол, равный внутреннему противолежащему с той же стороны, и внутренние односторонние углы «вместе» равны двум прямым» [Евклид 1948: 41]), а I éù K — определённые построения, преобразующие исходный треугольник, о котором идёт речь в предложении 32, в более сложную фигуру, к которой можно применить знание, выраженное в предложении 29 24. Именно так, как мы уже выяснили на анализе конкретных примеров, вырабатываются новые «необходимые» связи у Евклида, и именно эта особенность способа их получения определяет характер и способ всей организации геометрии как науки, её систему. Но здесь вполне закономерно поставить вопрос: насколько единственной и необходимой является такая система организации геометрии? И ответ, в принципе, может быть только отрицательным. После того, как предложения (ψ) → (φ), (μ) → (ν), (λ) → (x) … получены, их структурам, не меняя в общем и целом содержания самих предложении, можно придать такой вид и одновременно найти такие правила преобразования структур друг в друга, что мы получим «непрерывную» систему из всех имеющихся предложений, допускающую, теперь уже на основании иных принципов, все те переходы, какие были получены ранее на основе преобразования чертежей. Для этого надо, во-первых, изменить точку зрения на некоторые предложения — начать рассматривать их не как полученные путём анализа реальных явлений и реальных действий по отношению к предметам, а как предложения, допущенные гипотетически, без доказательств (так называемые «предметные аксиомы геометрии») 25, во-вторых, принять определённые правила преобразования предложений (ψ) → (φ), (μ) → (ν)… друг в друга (так называемые «логические аксиомы», или логические правила умозаключений), наконец, можно для достижения «непрерывности» ввести Тогда та же самая цепь «необходимых» связей знания, которая первоначально была получена на основе преобразования чертежей, примет вид:
Где ∑ [(A) → (B)] — набор «предметных геометрических аксиом», (ψ’) → (φ’), (μ’) → (ν’), (λ’) → (x’) — геометрические предложения, выраженные в словесно-алгебраической форме, соответствующей определённым логическим правилам преобразования, (f, k, (I)…) — сами эти логические правила, определяющие преобразование словесно-алгебраических выражений друг в друга. При этом система предложений ∑ [(A) → (B)] þ … [(λ’) → (x’)] разрывает свою связь о предметным содержанием геометрии — объектами-чертежами — и становится обособленной, самодовлеющей системой в теле науки. (Здесь требует самого тщательного анализа вопрос: теряется ли всякое содержание или только то, с которым эти формы были связаны первоначально?)
Но — и это нам особенно важно здесь подчеркнуть — внутри словесно-алгебраических фрагментов движение было одноплоскостным и подчинялась одним лишь логическим правилам выведения. Такое положение мы находим уже у Евклида. В дальнейшем удельный вес словесно-алгебраических фрагментов все более возрастает, всё большее число предложений принимает структуру, необходимую для чисто формального выведения, все отчётливее формулируются принципы формального подхода. Этот процесс можно явственно наблюдать по различным изложениям геометрии в XVIII–XIX столетиях. Наконец, в последней четверти ХIХ века «строго формальное», или, как стали говорить, аксиоматическое построение геометрии становится основным лозунгом работы геометров. Появляется целый ряд систем аксиоматического изложения евклидовой геометрии — М. Паша, Д. Пеано, Дж. Веронезе, М. Пиэри, Д. Гилберта и других. Идеалом для системы геометрии становится система абсолютно замкнутого формального исчисления, в котором структуры предложений имеют совершенно единообразный характер и получаются друг из друга путём чисто формальных преобразований в соответствии с правилами этого исчисления. Вот как, в частности, характеризует задачу своей работы сам Гилберт: «Основная мысль моей теории доказательства такова: все высказывания, которые составляют вместе математику, превращаются в формулы, так что сама математика превращается в совокупность формул. Эти формулы отличаются от обычных формул математики только тем, что в них, кроме обычных знаков, встречаются также и логические знаки: → & V — (x) (Ex) (следует, если — то) (и) (или, либо) (не) (все) (существует). Некоторые определённые формулы, которые служат фундаментом этого формального построения математики, называются аксиомами. Доказательство есть фигура, которая должна наглядно предстать перед нами; она состоит из выводов, делаемых согласно схеме:
В которой каждая посылка, то есть соответствующие формулы:
Каждый раз является либо аксиомой, либо совпадает с полученной ранее из доказательства формулой, или получается из такой формулы с помощью подстановки… Доказуемые теоремы, то есть формулы, получающиеся при этом способе, являются отображением мыслей, которые образуют обычную до сих пор математику» [Гилберт 1948: 366–367]. Затем Гилберт излагает принятые им логические правила, или аксиомы, явные определения и аксиомы рекурсии и добавляет: «В моей теории содержательные выводы заменены внешними действиями, подчиняющимися определённым правилам; тем самым аксиоматический метод получает ту надёжность и законченность, которая для него доступна и в которой он нуждается для того, чтобы служить основным средством теоретических изысканий» (там же, с. 369). Эту характеристику полезно сравнить с не менее резкой характеристикой Н. К. Рашевского, опубликованной через 32 года после доклада Д. Гилберта: «Предложения математики, равно как и законы логики, записываются при помощи особой символики в виде формул без всякого участия словесных выражений. Процессы логического мышления заменяются манипуляциями с такого рода формулами по строго очерченным правилам, а именно: из формул, уже построенных, разрешается чисто механически, по точно указанным рецептам составлять новые формулы, и это заменяет сознательные умозаключения, выводящие из одного предложения другое. Таким образом, и математическое, и логическое содержание исследуемого отдела математики предстаёт перед нами в виде цепи формул. Эта цепь начинается с формул, изображающих математические и логические аксиомы, и может быть неограниченно продолжаема путём механического составления новых формул. Нам нет при этом надобности понимать, какое математическое содержание записано под видом той или иной формулы; нас интересует лишь формула сама по себе как вполне конкретная и обозримая конечная комбинация знаков» [Рашевский 1960: 96] 26. Мы не можем сейчас входить в обсуждение вопроса о том, насколько точно и строго удалось Гилберту достичь желаемого идеала (с точки зрения принципов развиваемой нами содержательной логики многое выглядит совершенно иначе, нежели с точки зрения самих геометров и традиционных исследований по обоснованию геометрии 27), но в принципе такое преобразование системы геометрии вполне возможно, поскольку имеют дело с уже готовыми, наработанными предложениями и стоит задача лишь по-новому организовать их в систему. Кстати, здесь весьма характерно, что таких систем организации может быть очень много. Уже система Пеано, по определению Кутюра, была «логически безупречной» [Кутюра 1913: 161], хотя при целом ряде преимуществ, и не обладала достаточной логической общностью. Теория Пиэри, по выражению того же Кутюра, даже в сравнении с работами Гилберта, содержала «самый глубокий анализ принципов геометрии» (там же, с. 165–166). Примерно так же, с весьма относительных и односторонних позиций, оценивают в настоящее время и систему Гилберта: «Наиболее удачную, глубоко продуманную систему аксиом предложил Гилберт в своём сочинении «Основания геометрии». Эта книга выдержала длительное испытание временем, и в наши дни после ряда поправок система Гилберта остаётся наиболее целесообразной. Основная заслуга Гилберта, благодаря которой его труд стал классическим, заключается в следующем. Гилберту удалось сконструировать аксиоматику геометрии, расчленённую настолько естественным образом, что логическая структура геометрии становится совершенно прозрачной. Это расчленение аксиоматики позволяет, во-первых, формулировать аксиомы наиболее простым и кратким образом и, во-вторых, исследовать, как далеко можно развивать геометрию, если класть в её основу не всю аксиоматику, а те или иные группы аксиом, на которые естественным образом расчленяется аксиоматика» [Рашевский 1960: 81–82]. Приведённые характеристики достаточно отчётливо подтверждают наш тезис о том, что в аксиоматических построениях геометрии речь идёт о способах организации уже готового знания — множества геометрических предложений, а не о реконструкции способов образования или способов получения этих предложений. Таким образом, мы пришли к ответу на поставленный выше вопрос относительно роли словесно-алгебраических выражений в «геометрическом» мышлении, причём, что очень важно, к ответу, учитывающему историческое развитие геометрии. Сначала простейшие словесно-алгебраические выражения вида «равно», «неравно», «параллельно», «перпендикулярно», и так далее — возникают как средство и форма фиксации содержаний, выделенных путём определённых сопоставлений объектов-чертежей. Отношение между объектами-чертежами, связанными между собой отношениями сопоставлениями, и словесными выражениями может быть представлено как отношение между двумя различными плоскостями; геометрия, в силу этого, имеет двухплоскостную структуру. При этом основную часть, ядро и сердцевину геометрии составляют объекты-чертежи, поскольку «геометрическое движение» в этот период осуществляется только в форме сопоставления и преобразования чертежей; словесно-алгебраические выражения носят «вторичный» характер: они не являются «оперативной» частью геометрии. Структуру геометрии как системы образуют отношения сопоставления чертежей; эти отношения и составляют «единицы» нижней плоскости геометрии; словесно-алгебраические выражения разрозненны и являются элементами системы только за счёт своих связей с единицами нижней плоскости. Особый «чертежный» характер объектов геометрии, невозможность фактически накладывать их друг на друга делает необходимым анализ самих способов сопоставления объектов между собой. В результате этого анализа и разложения деятельности с объектами и учёта тех «сторон» объектов, на которые она непосредственно направлена, появляются сложные словесно-алгебраические выражения вида (b) → (a), содержащие «необходимые» связи между свойствами и соответственно знаками свойств. Благодаря этому в геометрии становится возможным другой вид движения: формальный переход по связям между элементами словесно-алгебраических выражений. На основе сопоставления и преобразования объектов-чертежей словесно-алгебраические выражения развёртываются в сложные цепи вида … (d) → (g) → (b) → (a). Движение по этим цепям, поскольку они уже сложились, может осуществляться без обращения к чертежам, по особым правилам, которые специально формулируются как логические правила умозаключения. Геометрия по-прежнему сохраняет двуплоскостную структуру, и в каждой плоскости существует свой вид движения: в нижней — содержательное движение, осуществляющееся в виде сопоставления и преобразования объектов-чертежей 28, в верхней — формальное движение, осуществляющееся в виде переходов по готовым цепям выражений, которые подчиняются логическим правилам. Цепи словесно-алгебраических выражений становятся относительно самостоятельными и относительно замкнутыми фрагментами системы геометрии. Но если брать систему геометрии как целое, то главными и основными в ней остаются пока всё же действия с чертежами: именно они связывают между собой фрагменты формальных переходов в одно целое, именно они образуют «скелет» системы геометрии. Наличие нескольких плоскостей и нескольких различных видов мыслительного движения, причудливо переплетающихся друг с другом, необходимость то и дело переходить с одной плоскости на другую, от одного вида движения к другому, создают, естественно, целый ряд затруднений при использовании геометрии для решения практических задач. Это обстоятельство стимулирует работу, направленную на то, чтобы преобразовать систему геометрии как целое, исключить из неё содержательное (а поэтому более трудное) движение в плоскости чертежей и оставить одно лишь формальное движение по цепям словесно-алгебраических выражений. Решение этой задачи знаменует собой превращение геометрии в замкнутое словесно-алгебраическое исчисление. Вместе с тем исчезает одна из её плоскостей — плоскость содержательных преобразований. Но было бы ошибкой сделать отсюда вывод, что геометрия становится одноплоскостной системой. Мы уже видели выше, что осуществление формального умозаключения предполагает определённые правила деятельности, и эти правила должны быть сформулированы в специальном языке, надстраивающимся над первым, формализуемым языком, и образующим в силу этого вторую плоскость системы. Потеряв нижнюю содержательную плоскость, на которую она «опиралась», формальная система приобретает другую, верхнюю — плоскость правил, к которой она как бы «подвешивается». Система по-прежнему остаётся двухплоскостной, хотя характер этих плоскостей существенным образом меняется. Именно на это преобразование системы геометрии опирался Л. Кутюра, полемизируя с И. Кантом, именно это он имел в виду, говоря, что геометрия не нуждается ни в каких фигурах, ни в каких построениях, она просто ссылается на предыдущие предложения и ограничивается сопоставлением и сочетанием их. «Реконструкция геометрии не есть просто идеальная возможность, а факт получивший воплощение в трудах современных геометров, — писал он в другом месте. — Итак, отныне установлено, что геометрические доказательства являются (то есть могут и должны быть 29) аналитическими и что вся геометрия может и должна быть логически выведена из каких-нибудь двух десятков постулатов» [Кутюра 1913: 251]. И как мы убедились из предыдущего анализа, нельзя сказать, что он неправ. Это было бы неверно, ибо современная система геометрии имеет именно такой характер, о котором говорит Кутюра. Но зато мы можем сказать, что все приведённые утверждения Кутюра, вся его полемика не имеют смысла. И мы будем иметь полное право сказать это, так как вся полемика Кутюра глубоко антиисторична, она совершенно не принимает во внимание того факта, что мышление в геометрии исторически развивается и при этом претерпевает такие изменения, которые в самом существенном меняют как его характер и структуру, так и характер всей системы геометрического знания. Кутюра совершенно не учитывает, что одно дело — процессы первоначальной выработки какого-либо общего положения в геометрии: они, в конечном счёте, всегда опираются на знаки-модели, на определённые фигуры, чертежи, и предполагает определённые содержательные действия по преобразованию и сопоставлению их; другое дело — применение этих общих, уже выработанных и словесно сформулированных положений к единичным случаям; здесь преобразования и сопоставления чертежей в самом этом процессе применения общих положений элиминированы, но сохраняются в скрытой форме, в ссылках на другие теоремы, излагающие способ получения этих положений; наконец, третье, существенно отличающееся от первого и второго, — новый способ организации и систематического изложения всей совокупности имеющихся знаний. Он связан с выработкой совершенно новых исходных знаний (аксиом, постулатов) и новых логических операций перехода от одних предложений к другим; вместе с тем этот процесс есть процесс перехода от системы с n языками к системе с n –1, n Именно этих различий, возникающих в ходе развития мышления, не учитывал Кутюра, а поэтому его полемика с Кантом и все оценки характера «геометрии вообще» не имеют смысла, являются, фактически, беспредметными: нужно было устранить историческую ограниченность точки зрения Канта, указав на развитие геометрии, изменение её структуры и методов, а вместо этого Кутюра выдвинул другую, столь же антиисторическую, а поэтому неизбежно одностороннюю и (в применении ко всей геометрии) неправильную точку зрения. Заканчивая обсуждение вопросов этого круга, мы можем сформулировать пятый вывод в плане непосредственно интересующих нас проблем: мышление в геометрии (и тем более мышление с помощью средств геометрии) обязательно имеет двухплоскостное строение; анализ его предполагает различение объектов и знаков, соответственно, плоскости содержания и плоскости знаковой формы — познавательных действий с объектами и действий со знаками, соответственно, движений в плоскости содержания и движений в плоскости знаковой формы; движения в плоскости знаковой формы в 16Может показаться странным, что, постоянно настаивая на этом последнем тезисе, мы с самого начала не положили его в основание всего анализа. Но это было не только оправданно, но даже необходимо. Приняв идею двухплоскостности в исходном пункте анализа, мы должны были бы вычленять в эмпирическом материале элементы плоскости содержания и элементы плоскости формы, ничего не зная ни о тех, ни о других. Временное отвлечение от идеи двухплоскостности, напротив, позволило нам выделить формальную часть рассматриваемого процесса мышления и Специально оговоримся: это расчленение ни в коем случае не может рассматриваться как точное и окончательное, оно должно быть уточнено и даже существенно исправлено на основе анализа содержательных частей процесса мышления, заключённого в рассматриваемом тексте, и выведения (функционального или генетического) из них формальных структур и операций. Но Всё это — дело второго этапа в исследовании заданного текста, а пока важно было получить хотя бы грубую основу. И она получена. Но теперь мы должны взглянуть на весь проделанный анализ с точки зрения принципа двухплоскостности и постараться выяснить, какие общие коррективы он вносит в его результаты. Вспомним основные шаги этого анализа. Исходным и определяющим для всего предшествующего было предположение, что процессы и операции мышления можно выделить, выделив их продукты — конечные знания и исходный материал, с которого начинает и на который опирается этот процесс. При этом предполагалось, во-первых, что исходный материал процесса мышления — это тоже знания, такого же вида и порядка, как и знания, являющиеся конечным продуктом этого процесса; во-вторых, — что знание есть то, что выражено какой-либо знаковой структурой вида «a = b», «a:b = c:d», и так далее (то есть являются образованиями одноплоскостными). Эти два предположения по существу были равносильны предположениям, что все операции и процессы мысли, во-первых, однородны по своей структуре, а во-вторых, сочленяются в линейные цепи через посредство своего исходного материала и конечных продуктов. Однако попытка провести анализ заданного текста на основе этих предположений, как мы теперь видим, натолкнулась на целый ряд трудностей. Прежде всего выяснилось, что понятие исходного материала, или исходного знания, с которого начинает «процесс», во всех мало-мальски сложных процессах мышления без дальнейших дополнений и уточнений «не работает». Оказалось, что в том виде, как мы его ввели, это понятие объединяет существенно различные по своей логической функции элементы процесса мышления. Чтобы преодолеть это затруднение мы различили собственно исходные и краевые знания. При этом в первом понятии фиксировались те знания, которые перерабатываются тем или иным процессом или теми или иными операциями в другие знания, а во втором — те обобщённые, безотносительные к частному содержанию знания, которые делают возможными сами эти операции и процессы мышления, превращая их в формальные действия и процессы. Однако и этого уточнения понятия «исходный материал» оказалось недостаточно. При первой же попытке выделить из заданного текста операцию, ближайшую к конечному продукту всего текста, мы обнаружили, что существует по меньшей мере два таких предложения, которые с равным правом могут претендовать на роль исходных знаний, а вместе с тем — и два различных процесса мышления, входящих в рассматриваемый текст, таких, что их нельзя расположить в линейный ряд. Так получила первый удар идея однородности операций мышления и их линейного сочленения. Нам пришлось сделать вывод, что анализируемый процесс мышления распадается на ряд относительно самостоятельных процессов мышления, связанных друг с другом как бы «перпендикулярно». Это было первым наиболее важным выводом из попытки применить намеченные в начале принципы содержательного функционального расчленения к конкретному тексту. Чтобы преодолеть обнаружившееся затруднение и продвинуть анализ дальше, мы вновь воспользовались понятием краевого знания — на этот раз беря его в более широком смысле, чем раньше — и ввели понятие о «краевых процессах мышления», которые входят в качестве необходимого элемента в рассматриваемый текст, но их анализ может быть выделен в особую и притом вторичную задачу по сравнению с анализом основной линии рассматриваемого процесса мышления. По существу это предположение было равносильно предположению, что процесс мышления в рассматриваемом тексте имеет структуру, по форме напоминающую ряд приложенных друг к другу букв Т, то есть схематически фигуру вида:
Где горизонтальная линия изображает основную линию процесса мышления, а вертикальные линии — краевые процессы. Мы предположили также, что краевые процессы независимы друг от друга и единственное, что объединяет их в одно целое, в один процесс мышления — это основная линия, которой они подчинены и от которой зависят. Но здесь нас ждала новая неожиданность. Когда мы, оставив пока в стороне краевые процессы, приступили к анализу основной мыслительной линии текста, то оказалось, что в ней нет именно того, что мы ищем — нет самого процесса мышления. Прежде всего это проявилось в том, что мы не смогли определить «направление» происходящего по ней движения. Если судить непосредственно по языковому тексту, то движение мысли происходит слева направо, от известного к искомому, то есть к ответу на вопрос всей задачи. В то же время уже самые поверхностные соображения убеждают в том, что реальный мыслительный процесс решения задачи должен был бы иметь противоположное направление: от вопроса, который в определённом отношении характеризует и сам ответ и способ его получения, к тем данным, на основе которых можно получить конкретную форму этого ответа. Мы предположили, что истинный мыслительный процесс идёт именно в этом, последнем направлении, и выяснили, что по смыслу он должен быть переведением математического отношения искомых величин в математическое отношение двух других величин, которые уже известны или могут быть определены. Одновременно мы выяснили, что необходимым условием переведения является выработка особого знания — математического соотношения, которое выступает в качестве краевого знания для самого переведения и получается с помощью того процесса мышления, которое мы отделили в качестве краевого от основной линии текста. Но после того, как это знание получено — и в этом состояла парадоксальность всей ситуации, — переведение как мыслительный процесс (по схеме направленный справа налево) уже не осуществляется, а вместо него осуществляется другой процесс, который мы назвали переносом и который является чисто формальным движением, совершаемым по уже готовым связям знания и в соответствии с обобщёнными формальными правилами. Таким образом, выяснилось, что в основной, «горизонтальной линии» текста нет собственно процесса мышления. Этот вывод поставил под сомнение начальные понятия исходного и конечного знания, а вместе с тем и само понятие мыслительной операции. Действительно, является ли «переведение» операцией мышления? И если это — операция, то где её «тело» и как определить её состав? Ведь это такая операция, которая реально, по меньшей мере в разобранном тексте, не осуществляется. И с другой стороны: можно ли перенос считать мыслительной операцией? И если да, то как он относится к операции переведения? И более общий вопрос: как относятся друг к другу «содержательные» и «формальные» операции? Во всяком случае, результат, полученный из этой попытки применить исходные принципы содержательного функционального разложения к эмпирическому тексту, убедительно показал, что предположение об однородном характере операций в сложных процессах мышления неверно, и поставил в качестве наиболее важной проблемы вопрос о видах этих операций и их взаимных отношениях; он выдвинул на передний план понятие «задача» и показал необходимость исследовать особые мыслительные движения, заключающиеся в смене задач, безотносительно к осуществлению процессов мышления, связанных обычно с их решением. Это было вторым наиболее важным результатом предшествующего анализа. Не обнаружив процессы собственно мышления в основной линии текста, мы должны были затем в соответствии с исходным планом анализа рассмотреть один за другим все краевые процессы, с тем чтобы попытаться «ухватить» мышление в них. При этом оказалось, что все тексты, соответствующие этим процессам мышления, содержат ссылки на специфически геометрические знания и очень часто непосредственно на геометрические чертежи и построения. Понять структуру этих мыслительных процессов без анализа природы геометрических чертежей и их роли в этих процессах было невозможно, и таким образом мы оказались вовлечёнными в весьма длительное и пространное исследование строения мышления в собственно геометрии. Основным видом этого исследования (в интересующем нас сейчас плане) было положение, что процесс собственно мышления в геометрии обязательно имеет как бы двухплоскостное строение, что анализ его предполагает функциональное различение объектов и знаков и соответственно познавательных действий с объектами и действий со знаками. Если на первом этапе нашего анализа мы не учитывали этого обстоятельства и это позволило нам выделить формальную часть рассматриваемого процесса мышления, то теперь, когда формальная часть уже выделена и мы переходим к анализу той части текста, которая, по предположению, должна содержать собственно мышление, отвлечение от фактора двухплоскостности становится, очевидно, уже недопустимым. Поэтому, переходя в соответствии с намеченным выше планом исследования к анализу краевых процессов, мы должны попытаться выделить в них специфически мыслительные двухплоскостные структуры движений. Но здесь встаёт ряд принципиальных методических проблем. Мы выделяем три. Во-первых, как сочетать начальный принцип выделения конечного и исходного знания с новым принципом двухплоскостности? В частности, возникает вопрос: с рассмотрения какой плоскости надо начинать анализ? Во-вторых, какова структура простейших операций мысли? Если до сих пор, рассматривая операции мысли как чисто линейные образования, мы могли не ставить этот вопрос, так как тот или иной ответ на него нисколько не влиял на метод анализа сложных процессов мысли, то теперь, в свете тезиса о двухплоскостности процесса мысли, он приобретает первостепенное значение, так как, абстрактно говоря, становятся возможными различные способы связи операций в сложном процессе мысли и соответственно различные схемы анализа. В-третьих, сохраняет ли рассматриваемый процесс мысли своё Т-образное строение при разложении его на двухплоскостные единицы? Ведь мы пришли к изображению процесса в виде основной и ряда краевых линий в результате попыток представить его как гладкую последовательность линейных единиц. Может быть, этот результат был следствием неадекватности нашего понимания и методов анализа действительному строению процесса мысли и после изменения исходящей гипотезы окажется, что процесс представляет собой линейную последовательность двухплоскостных образований? Обсудим все эти вопросы, так как тот или иной ответ на них имеет первостепенное значение при поиске элементов и единиц сложных процессов мысли. При этом первый и второй будем по возможности объединять. 17Начнём с анализа эмпирического материала. Возьмём, к примеру, первый из намеченных нами краевых процессов. В тексте Аристарха он выражается лаконической фразой: «Из подобия треугольников SLT и TEH следует, что EH:TH = LT:ST». Эту фразу, в зависимости от направленности анализа, можно понимать двояко:
В обоих случаях эти формулировки неточно выражают возможный процесс, и в то же время каждая из них отражает какую-то его реальную сторону. Рассмотрим более подробно эти понимания. Прежде всего бросается в глаза, что из знания «Треугольники SLT и TEH подобны» совсем ещё не следует знание «EH:TH = LT: ST». Поэтому если мы хотим рассмотреть соответствующее движение в плоскости более точно, то мы прежде всего должны более точно выделить сами знания, участвующие в этом процессе. Таких знаний будет несколько. Это, во-первых, единичное знание «Треугольники SLT и TEH подобны», во-вторых, единичное знание «EH, TH, LT, ST суть соответственные стороны подобных треугольников SLT и TEH», в-третьих, общее знание «Если треугольники подобны, то отношения их соответственных сторон равны» и, наконец, в-четвёртых, единичное знание «Отношение EH к TH равно отношению LT к ST» (или, что то же самое, «EH:TH = LT:ST»). Выделив эти знания, можно попытаться схематически изобразить движение в них. Для этого мы воспользуемся вначале символикой, похожей на традиционную символику математической логики, и интересующий нас процесс предстанет примерно в таком виде:
Где (A, B) P изображает первое из названных выше знаний, причём А и В есть изображение «предметов» этого знания — треугольников, а P — знак их предиката «подобны»; (a, b, c, d) Q изображает второе из названных выше знаний, причём a, b, c, d есть изображения «предметов» этого знания — сторон треугольников, а Q — знак их предиката «соответственные»; символическое выражение, стоящее во второй, верхней, линии изображает третье из указанных выше знаний, причём, горизонтальная стрелка в этом выражении есть знак импликации; левая от стрелки часть содержит те же предикаты, что и левая часть нижней линии, но вместо постоянных там находятся знаки переменных, то есть другими словами, это — часть функции-высказывания; правая от стрелки часть содержит предикат «равны» (L), а «предметами» этой части высказывания являются математические отношения переменных (любых соответственных сторон подобных треугольников); наконец, выражение (arb, crd) (L) изображает последнее, четвёртое, из названных выше знаний, причём, arb и crd суть изображения «предметов» этого знания — математических отношений величин сторон подобных треугольников, а (L) в соответствии с уже сказанным выше есть знак предиката «равны», относящегося к этим предметам-отношениям. Характерным для такого подхода к исследуемому движению является то, что все знания, кроме последнего, четвёртого, как общие, так и единичные, рассматриваются как уже готовые, полученные. Но это, как мы уже не раз показывали выше, означает, фактически, что отсекается собственно процесс мышления, или, точнее, его наиболее важная объективная или содержательная часть и для рассмотрения остаются одни лишь «формальные действия». Поэтому, если мы хотим исследовать сами процессы мышления в их целостности, то должны выделить в качестве особого предмета и зафиксировать в особых знаках такие процессы получения знаний, при которых эти знания в конечном счёте получаются не из других знаний, а непосредственно на основе действий с объектами. Здесь, правда, возникают исключительно важные общие вопросы: а всегда ли это можно сделать? не выльется ли эта процедура в бесконечную? и так далее. Но мы сейчас не будем обсуждать их в общем виде, и ограничимся анализом одного рассматриваемого случая. Здесь задача сводится к анализу процессов получения трёх знаний: одного общего — импликации (Х, Y) P × (v, w, x, y) Q → (v, r, w, xry) и двух единичных — (L) (A, B) P и (a, b, c, d) Q. Однако общее знание представляет собой общественно фиксируемую форму, оно получается в процессе генетического формирования геометрии как науки и в каждом частном процессе мышления берётся как готовое; в данном случае оно выступает как общественно фиксированное условие всего рассматриваемого движения, следовательно, как краевое знание (в узком смысле этого слова), и поэтому анализ процесса его получения должен быть вынесен за пределы проводимого исследования. Остаётся, следовательно, анализ процессов получения двух единичных знаний. И здесь не трудно заметить, что они оба могут быть получены только на основе анализа самих реально заданных подобных треугольников, и при этом — путём весьма простых познавательных действий. Таким образом в данном случае сведение знаний к действиям непосредственно с объектами оказывается вполне осуществимым и притом — весьма коротким путём. Но это значит, что в выражении «Из подобия треугольников SLT и TEH следует…» оказывается больше правды, чем в первой из наших интерпретаций: знание «EH:TH = LT:ST» получается из анализа подобия самих реальных треугольников. Но и в этом выражении содержится по меньшей мере неточность. В частности, слово «следует» имеет здесь слишком широкий смысл, и если его раскрывать, то мы наталкиваемся на массу разнородных движений. Так, знание «EH:TH= LT:ST» можно получить на основе анализа подобия треугольников SLT и THE только с помощью определённых формальных средств, в частности, только с помощью общего знания «Если треугольники подобны, то отношения их соответственных сторон равны». Поэтому мы и сказали выше, что обе эти интерпретации, оба эти понимания правильно отражают разные реальные стороны дела, но каждое — очень неполно и неточно. Их нужно попытаться объединить друг с другом. Это можно сделать, добавив к уже имеющейся схеме ещё одну часть, изображающую сами объекты — треугольники, их отношения и связи, — а также познавательные действия, направленные на эти объекты и выявляющие их свойства. Тогда схема рассматриваемого мыслительного движения примет примерно такой вид:
В пояснениях здесь нуждается лишь новая, нижняя строка схемы. Буквы А и В в ней изображают сами треугольники — объекты (данные в чертежах); знак R1 и знаки фигурных скобок показывают, что между этими треугольниками существует особое объективное отношение, причём фигурные скобки указывают, какие именно объекты охвачены отношением, а R1 указывает на вид отношения; знак D1 (читается «дельта один») изображает познавательную операцию, выделяющую определённое свойство этого отношения; горизонтальная скобка показывает, что объект, к которому применяется познавательная операция D1, есть все это отношение R1{A B} в целом. Во втором столбце применяется тот же принцип обозначения, то есть буквы a, b, c, d изображают сами стороны — объекты (данные в чертежах) — и так далее. Выше мы не случайно оговорились, что воспользуемся традиционной символикой математической логики только для начала. Фактически мы уже значительно преобразовали её, дополнив специальными изображениями объектов, их взаимоотношений и знаками познавательных действий. Но две верхних строки схемы остались неизменными. Это, конечно, непоследовательно. И в дальнейшем мы подвергнем критике сам способ такой символизации и такого представления рассматриваемого краевого процесса и покажем, в каких отношениях он неудовлетворителен. Но вместе с тем этот способ, с одной стороны, безусловно верно схватывает определённые стороны анализируемого мыслительного движения, и поэтому приведённая выше схема позволяет более детально обсудить и отчётливее понять их, а с другой стороны, этот способ символизации рельефно обнаруживает недостатки применяемого математической логикой подхода, и это тоже может быть обнаружено на этой схеме. Таким образом, мы начали с предложения из текста Аристарха Самосского и попытались, используя уже существующие традиционные схемы, изобразить скрывающийся за ним процесс мышления. Это были одновременно как попытка ответить на вопрос о строении простейших процессов мысли, так и попытка выработать метод введения объектов в схемы их изображений. Посмотрим, насколько сама схема отвечает нашим представлениям о процессе мысли. Первый вопрос, который здесь должен быть задан и которым мы уже не раз начинали анализ выделенных процессов мысли: насколько правильно эта схема изображает направление действительного процесса мышления? И обсуждение его повторяет всё то, что уже говорилось в отношении других процессов мысли. С одной стороны, казалось бы, процесс установления математического соотношения «EH:TH = LT:ST» идёт именно в том направлении, как это указано на схеме. Но, с другой стороны, стоит только подойти к этому процессу с точки зрения всей схемы решения исходной задачи, как тотчас же становится очевидным, что собственно процесс мышления должен иметь противоположное направление — от задачи установить такое соотношение к поиску средств, позволяющих её решить. Как и раньше мы пытаемся обойти проблему — именно не разрешить, а обойти, — вводя различение двух движений:
При этом общий характер и строение первого движения остаются совершенно неясными. Во всём предшествующем изложении мы только ставили задачу проанализировать это движение, но не делали никаких реальных попыток осуществить сам анализ. Второе движение, напротив, выглядит значительно более простым и понятным и, Поэтому и здесь мы начнём с обсуждения именно его. 18По структуре, зафиксированной на схеме, это движение очень напоминает процесс соотнесения, который в простейшем случае (в подобной же символике) изображается так:
Отличается оно от процесса соотнесения (что тоже можно видеть из сравнения схем), во-первых, тем, что в него входит целый ряд различных объектов — А, B, a, b, c, d, arb, crd, — а во-вторых, тем, что нет последнего акта отнесения выражения к объекту. От первого обстоятельства мы пока отвлечемся, считая, что оно не меняет общей принципиальной схемы процесса и может быть учтено путём последующей восходящей конкретизации; эту конкретизацию мы постараемся в дальнейшем проделать. Второе обстоятельство определяется назначением и ролью процесса мышления. Смысл и назначение процесса соотнесения в том, чтобы приписать непосредственно объекту Х свойства, зафиксированные в выражении (a) (L). Это и есть собственно то, что определяет специфику и целостность процесса соотнесения. Рассматриваемый краевой процесс, напротив, не является самостоятельным процессом мысли, он есть лишь часть сложного процесса решения задачи и «работает», как мы уже отмечали, на В соответствии с этим выводом мы должны будем вернуться к анализу этой стороны рассматриваемого движения ниже, а пока предположим, что языковое выражение (arb, crd) в нём относится к своим объектам точно так же, как и выражение (a) (L) в процессе соотнесения, и будем считать, что такое предположение не создаёт принципиальной методической ошибки и мы сможем его «исправить» путём конкретизации на последующих этапах анализа. Итак, в первом приближении мы можем считать, что рассматриваемый нами процесс по общей схеме подобен процессу соотнесения. Охарактеризовав таким способом структуру рассматриваемого движения, мы можем теперь попытаться решить ряд важных вопросов общего порядка и, в том числе, вопрос относительно того, как сочетается начальный принцип выделения конечного и исходного знания с принципом «двухплоскостности». С точки зрения схемы процесса соотнесения рассматриваемое нами движение содержит три языковых выражения, за которыми могут скрываться знания и которые, в соответствии с общими принципами анализа, выделяются нами при выделении процесса мысли из эмпирически заданного текста. Это выражения: (a) P, (Х) P → (Х) (L) и (a) (L). С точки зрения структуры процесса соотнесения они не однородны и играют разную роль в мыслительном движении: первое и третье являются выражениями, фиксирующими действительные единичные, или, как мы говорим, реальные знания об объектах, а второе не может быть непосредственно отнесено к объектам и поэтому не может рассматриваться как выражение реального знания; оно имеет так называемое общее значение и является формальным знанием (или, как нередко говорят, схемой или формулой особого мыслительного действия). В исходных принципах содержательного анализа мы не делали различия между этими двумя видами выражений (и, собственно, на этом этапе исследования и не могли этого делать), но при первом же столкновении с эмпирическим материалом вынуждены были ввести его, указав на различие собственно исходных и краевых знаний. Теперь мы видим, что это различение оправдывается не только соображениями удобства анализа, но и соображениями, исходящими из уже проделанного анализа «внутренней» структуры самих процессов мысли. Мы видны также, что в данном мыслительном движении, если рассматривать его как подобное процессу соотнесения, есть всего два знания в точном смысле этого слова, то есть всего два выражения, отнесённых к объектам:
А краевое знание (Х) P → (Х) (λ) является лишь формальным выражением. Поэтому, формулируя в начальных принципах метода требование — при эмпирическом анализе текста для выделения процесса мысли необходимо найти всего два знания: исходное и конечное — мы поступали, если отвлечься от возможностей разветвления самого сложного процесса, совершенно правильно. Но это требование оставалось недостаточно точным и однозначным, пока мы не пополнили его принципом двухплоскостности, указывающим, что действительное знание всегда содержит отнесённость к объектам, и дающим в силу этого основание для различения реальных и формальных знаний, соответственно реальных и формальных выражений. Именно в принципе двухплоскостности содержится теоретическое обоснование этого различения. Вот один важный вывод, уточняющий исходные принципы функционального расчленения процессов мысли. Приостановим на этом анализ выделенного краевого процесса с точки зрения входящих в него знаний (с тем, чтобы вернуться к нему ещё раз в дальнейшем) и попробуем взглянуть на этот процесс с иной точки зрения: в плане состава самих действий и мыслительных операций. Если судить по записанной выше схеме, то процесс соотнесения, а вместе с ним в первом приближении и анализируемый краевой процесс могут и должны состоять из пяти «переходов»: 1) от Х к (a) P (мы обозначаем сам этот переход знаками D и ); 2) от (a) P к (Х) P → (Х) (L); 3) от (Х) P → (Х) (L) к (a) (L) (в этих двух случаях сами переходы мы никак не обозначаем); 4) внутри самого формального выражения от (Х) P к (Х) (L) (условно можно считать, что сам переход в этом случае обозначен горизонтальной стрелкой, то есть знаком импликации), и, наконец; 5) от (a) (L) к Х (здесь сам переход обозначен вертикальной стрелкой вниз). Такой вывод является фактически необходимым, если мы будем исходить из приведённой выше схемы, из понимания, лежащего в её основе и её символических средств. Но по сути, ни один из этих переходов не может рассматриваться как истинное действие и тем более как операция или процесс мысли. Действительно, переход от Х к (a) P, если следовать смыслу самой схемы, есть фактически не что иное, как связь внутри единичного знания Х — (a) P, которое мы рассматриваем как одно целое, с которого, по предположению, начинается анализируемый процесс мысли. Поэтому, чем бы ни была фактически операция по получению знания Х — (a) P, с точки зрения схемы, взятой в соединении с исходными принципами нашего анализа, этот переход не является собственно движением и тем более операцией мысли. То же самое нужно сказать относительно перехода от (a) (L) к Х. (Х) P → (Х) (λ) по смыслу всего исходного анализа и схемы есть готовое знание, которое в рассматриваемом процессе остаётся неизменным и служит лишь схемой для перехода от (a) P к (a) (L). Никакого перехода от (Х) P к (Х) (L) мы фактически не имеем. Остаются два перехода: от (a) P к формальному выражению (Х) P → (Х) (L) и от него к (a) (L). В математической логике этот переход называют обычно подстановкой постоянных в логическую функцию. В Из этого анализа прежде всего напрашивается вывод, что символика современной математической логики и схемы, построенные на этой символике, не могут быть использованы при попытках проанализировать процессы мысли с точки зрения состава входящих в них операций (во всяком случае, на основе тех понятий знания, процесса и операций, которые мы ввели). Несколько более удачной оказывается символика, которая, основываясь на идее двухплоскостности и используя для изображения её нелинейные (в частности, двухмерные) схемы, отбрасывает понятия постоянных и переменных и знаки для их изображения и таким образом возвращается по форме к классическим Аристотелевым схемам 30. Средствами этой символики (при том же принципе подхода к процессам мышления с точки зрения входящих в них знаний) процесс соотнесения можно будет изобразить так:
Это даст известное облегчение в понимании действий, входящих в мыслительный процесс соотнесения, так как позволяет интерпретировать переходы от Х — (A) к (A)–(B) и от последнего к (B) — Х соответственно как объединение знаний по тождеству терминов и исключение термина, опосредствующего связь между Х и (B). Это позволяет также представить анализируемый процесс мысли как комбинацию из двух мыслительных операций (первая за счёт действия объединения осуществляет переход от реального знания Х — (A) к реальному же знанию Х — (A)–(B), а вторая за счёт действия исключения — переход от знания Х — (A)–(B) к третьему реальному знанию Х — (B), чего нельзя было сделать, пользуясь прежней символикой. Но и такое представление мыслительных операций остаётся во многом весьма сомнительным. Прежде всего указанное изменение символики, по-прежнему фактически всецело основанное на принципе изображения не мыслительных операций как таковых, а только их продуктов-знаний, и фиксирующее сами операции в неявном виде, как переходы от одних знаний к другим, происходящие за счёт чисто механических действий типа объединения и исключения, не решает проблемы формальных и реально-содержательных движений, которую мы уже не раз затрагивали выше. Ведь фактически то требование, В то, что отсекается таким подходом, входит, во-первых, процесс получения исходного знания, во-вторых, фактически, и процесс получения конечного знания, потому что выражение (a) (L) или, по новой схеме, (B), становится формой фиксации определённого знания только при отнесении его к объектам, а это отнесение представляет собой движение отнюдь не тождественное «исключению», а значительно более сложное и определяемое какими-то содержательными параметрами; в зависимости от них оно будет или не будет осуществлено (на этот факт мы уже указывали, сравнивая процесс соотнесения с анализируемым нами краевым процессом). Но если это конечное движение, осуществляющее отнесение языкового выражения (a) (L), или (B), к определённым предметам, оказывается за границами исследуемого нами, то это фактически означает, что и все рассматриваемое движение не является процессом мышления в точном смысле этого слова, так как оно не даёт и не может дать в качестве своего продукта собственно знания. Таким образом, здесь, в заключительном акте выделяемого мыслительного движения мы не можем ограничиться исследованием только перехода от (Х) P → (Х) (L) к (a) (L) или действия исключения, как осуществляющего переход от знания Х — (A)–(B) к знанию Х — (B), а должны будем также подключить учёт и анализ Но этот вывод ставит перед нами действительно сложную проблему и заставляет сделать исключительно важные методологические выводы. Ведь если в качестве процесса мысли (в его операциональном составе) мы должны рассматривать все движение, изображённое на схемах 33 и 34, то исходным и конечным материалом этого процесса, а вместе с тем исходным материалом одной входящей в его состав операции и «конечным материалом» другой, может быть только сам объект Х, а отнюдь не знания об этом объекте. Этот вывод является исключительно важным, он влечёт за собой необходимость пересмотра или, во всяком случае, уточнения целого ряда положений, выдвинутых выше. Во-первых, он ещё раз указывает на неоднородность состава многих процессов мышления и, в частности, при анализе процесса соотнесения заставляет, Первые предполагают в качестве своего условия простую форму, не содержащую связи значения и предназначенную только для фиксации выделенного в объектах содержания, вторые предполагают сложную форму или формальное знание, обязательно со связью значения, позволяющей переходить от одного элемента формы к другому. Первые выделяют в единичных объектах определённое содержание, вторые приписывают им Одним словом, первые являются собственно познавательными, мыслительными операциями, вторые — играют роль таких операций в контексте процесса соотнесения. Во-вторых, этот вывод и основанное на нём различение реальных и формальных операций заставляет нас ещё раз существенным образом уточнить понятие исходного материала, введённое при изложении начальных принципов метода. Там мы отождествляли исходный материал со знанием. В определённых границах это было оправданным и даже необходимым: оно дало нам возможность хотя бы грубо отграничить друг от друга различные части внутри рассматриваемого нами сложного процесса мышления и проанализировать строение этих частей с точки зрения состава входящих в них языковых выражений. Успех этого этапа анализа, пусть относительный, служит достаточным подтверждением правильности этого отождествления как первого приближения в решении вопроса. Но вместе с тем дальнейший анализ показал, что такое понимание исходного материала, даже после того, как на основе принципа двухплоскостности мы уточнили само понятие знания, неизбежно приводит к тому, что мы ограничиваем сам процесс мышления, если брать его с точки зрения состава операций, только формальным движением и не можем схватить объективно-содержательных операций. Ведь последние как раз характеризуются тем, что они начинают не с готовых языковых выражений, а с самих объектов, и поэтому, естественно, выпадают из сферы анализа, если мы ограничиваем исходный материал одними лишь знаниями. Следовательно, чтобы иметь возможность охватить анализом также и реальные мыслительные операции, мы должны расширить понятие исходного материала, сказав, что для одних операций — формальных — им являются знания, а для других — реальных — сами объекты. Первое определение исходного материала не давало нам возможности выявлять реальные операции и исследовать их структуру, в частности, все то в этих операциях, что относилось к «нижней» плоскости объектов и действий с ними. Поэтому произведённое уточнение понятия исходного материала является исключительно важным: только оно даёт возможность выделить ту действительность, в которой лежат реальные операции. Но применить его в ходе анализа самого текста оказывается не так-то просто. Дело в том, что в языковом тексте как таковом мы не можем найти и выделить сами объекты. Выявление их, и то лишь в подразумеваемом плане, возможно только на основе сложного смыслового анализа текста, учитывающего кроме того весьма необычные логические характеристики объекта (более подробно мы будем говорить об этом несколько ниже). Поэтому употреблять это различение непосредственно на первом этапе анализа текста невозможно. Единственное, что мы можем и должны сделать в плане уточнения методологии этого этапа анализа, — это указать на то, что сам исходный материал процесса мысли сложен и неоднороден по своему составу и что требование найти исходный материал какого-либо процесса означает, что в общем случае надо найти по меньшей мере четыре различных его компоненты:
Элементы, перечисленные под пунктами 2); 3) и 4), дают нам фактически структуру исходного знания, то есть то, что мы с самого начала фиксировали в понятии исходного материала. Элементы, идущие под пунктом 1), при первом уточнении были вынесены в краевое знание, но теперь могут быть охарактеризованы как особые элементы исходного материала. Перечисляя элементы исходного материала, мы отнюдь ещё не выявляем операцию, приводящую к образованно исходного знания, и тем более не делаем шагов в анализе структуры этой операции; мы только указываем, что за этим и именно за этим знанием должна скрываться «реальная» операция мышления. Тем самым мы выделяем предмет для второго этапа анализа текста, который направлен на выяснение структуры реальных мыслительных операций и начинается лишь после того, как выделены, обозначены и тем самым отграничены друг от друга все процессы и операции, входящие в анализируемый текст. Каким должен быть такой анализ — этот вопрос мы будем обсуждать в другой связи, здесь же нам важно лишь уточнить само понятие исходного материала. В-третьих, сделанный выше вывод о характере исходного и конечного материала процесса мышления позволяет Достаточно так поставить вопрос, чтобы стало ясным, что решение его должно вылиться в длительное и трудное исследование операциональной структуры процесса соотнесения и многих других процессов мысли. Дело затрудняется ещё и тем, что мы пока не начинали систематического исследования ни структуры, ни функций этих операций и, более того, по характеру нашего нынешнего движения даже не можем мечтать о таком исследовании. Всё это — задача восходящего генетического выведения. А пока мы не знаем ни структуры, ни функций операций, выделенных в процессе соотнесения, и у нас нет подходящей символики для их изображения, но мы должны знать, какие операции и процессы мысли являются целостными, а какие нет, так как от этого во многом зависит весь наш дальнейший функциональный анализ. В этих условиях, как оказывается, можно использовать в качестве критерия целостности операций и процессов мысли сформулированное выше положение о том, что исходным и конечным материалом процесса мышления должны быть сами объекты, и таким путём решить проблему, обойдя задачу исследовать способы сочленении операций внутри процессов. Этот подход становится особенно ясным, если воспользоваться для пояснения схематическими изображениями. Например, в процессе соотнесения:
Ни одна из выделенных выше операций, включая и первую — реальную, с точки зрения этого определения не является целостным процессом мысли: первая, если брать её изолированно, не содержит обратного движения к объекту, вторая, взятая отдельно, не имеет объекта ни в своём начале, ни в конце, а третья, опять-таки если рассматривать её саму по себе, не имеет начального движения от объекта. Но та же самая первая операция станет целостным процессом мысли, если она будет осуществляться не в контексте процесса соотнесения, а сама по себе и для себя. В этом случае она будет содержать как прямое движение от Х к знаку (A), так и обратное движение от (A) к Х, и её нужно будет изобразить в схемах
Если описывать наглядный вид самой схемы, то можно сказать, что целостным процессом мысли являются операции или комбинации операций, представляющие собой как бы «замкнутые кольца». Подобным же целостным процессом мысли может стать комбинация из первой и второй операции в том случае, когда мы будем относить к объекту Х все формальное выражение (A) → (B). Схематически этот процесс можно будет изобразить примерно так:
В свете этих положений о целостности и частичности операций и процессов мысли мы можем Поэтому они всегда остаются частичными мыслительными операциями и могут образовывать процессы мышления только в связи с какими-либо реальными операциями. Этот вывод позволяет нам также утверждать, что формальные операции нельзя рассматривать в одном ряду с «реальными», собственно мыслительными операциями или с целостными процессами мышления. Обобщая анализ процесса соотнесения, мы можем сказать, что вместе с реальными операциями (одной или несколькими) в один сложный процесс мышления могут сочленяться не только две формальные операции из действий типа «объединения» и «исключения», но, очевидно, и целые цепи их, которые схематически можно будет изобразить так:
И какими бы длинными ни были эти цепи, и они всегда будут представлять собой единый целостный процесс, если только у них будет всего одно движение от объекта и одно «возвращение» к объекту, и каждый раз такой процесс мысли будет представлять собой как бы замкнутое циклическое движение 31. Этот вывод значительно продвигает нас в понимании возможного строения одного из простейших процессов мысли, а именно процесса соотнесения, и даёт некоторое вспомогательное средство для анализа других, более сложных процессов. Вместе с тем, мы ещё очень мало продвинулись как в выяснении того, что такое объект знания и каковы методы его выявления, так и в анализе эмпирически заданного нам текста. Поэтому мы должны вернуться к рассматриваемому краевому процессу. 19Все выводы предыдущего параграфа были получены нами в предположении, что рассматриваемый краевой процесс (I) (см. схемы 6 (1), 31, 32) подобен процессу соотнесения и что, следовательно, всё то, что мы говорим о последнем, будет справедливо и в отношении первого. Производя это замещение, мы в то же время подчёркивали, что на самом деле рассматриваемый краевой процесс по меньшей мере в двух существенных моментах отличается от процесса соотнесения и что поэтому тезис об их подобии может быть принят только в первом приближении. Но само это приближение, считали мы, возможно, так как между сторонами краевого процесса, которые мы рассматривали в модели процесса соотнесения, и теми сторонами, от которых мы сознательно отвлекались, существует отношение абстрактного и конкретного, и, следовательно, опущенные пока особенности краевого процесса могут быть учтены на втором этапе анализа путем конкретизации характеристик процесса соотнесения. Теперь мы должны осуществить эту конкретизацию. Для этого прежде всего, в соответствии с соображениями, изложенными в предыдущем пункте, упростим символику, посредством которой мы изображали анализируемый краевой процесс. Его схема будет выглядеть тогда так:
От предыдущей схемы она отличается только тем, что опущены знаки переменных и постоянных и добавлена штриховая стрелка вниз от (L), обозначающая условное отнесение (L) к его предполагаемому объекту:
Теперь сопоставим между собой схемы краевого процесса (I) и процесса соотнесения и постараемся выяснить, что представляют собой те стороны исследуемого краевого процесса, от которых мы отвлеклись на первом этапе анализа. С самого начала бросается в глаза то обстоятельство, на которое мы уже указывали выше, при сведении краевого процесса к процессу соотнесения: различие между ними в количестве и характере объектов. В процессе соотнесения имеется всего один объект, в краевом процессе — несколько. Пока трудно сказать, сколько именно, так как ещё недостаточно выяснены критерии выделения и определения объектов в сложных мыслительных процессах, но, во всяком случае, это можно утверждать с уверенностью, — не один. Другое обстоятельство, тоже с самого начала бросающееся в глаза, это различие в количестве знаний, которые могут рассматриваться как собственно исходные, и, соответственно, в количестве реальных операций, создающих эти знания. В процессе соотнесения имеется всего одно исходное знание, и соответственно этому мы выделяем в нём всего одну реальную операцию. В краевом процессе (I) таких знаний и операций несколько. Мы опять-таки не можем с уверенностью сказать, сколько именно, так как не имеем необходимых критериев для разложения сложных знаний на простые составляющие. Но характерно, что уже самый поверхностный подход позволил нам выделить в рассматриваемом краевом процессе два исходных знаний (если не две группы таких знаний!). А более точный ответ требует специального анализа эмпирического материала и выработки новых логических понятий. Попробуем сделать это, опираясь на эмпирический материал. При первом подходе к краевому процессу (I) мы выделили в нём два собственно исходных звания: 1) утверждение относительно треугольников TEH и SLT — что они подобны и 2) утверждение относительно сторон EH, TH и LT, ST — что они соответственные. Эти два знания схематически в упрощённой символике были изображены как:
Но почему именно эти знания были выделены в качестве исходных, в чём основание для такого именно анализа и изображения первой части рассматриваемого краевого процесса? Ведь можно произвести совершенно другое расчленение и выделить, к примеру, такие знания:
Тогда в рассматриваемом краевом процессе оказалось бы сразу восемь исходных знаний, и мы должны были бы искать, соответственно, восемь реальных операций, создающих эти знания. Но и приведённое выше разложение не является окончательным. Так, нетрудно заметить, что знание (7) является сложным, что оно само получается опосредствованным путём, по структуре очень напоминающим процесс соотнесения, и что, следовательно, при более тщательном анализе этот процесс должен будет дать (кроме общего формального знания) целый ряд единичных реальных и поэтому в определённом смысле «исходных» знаний. При одном из возможных вариантов это будут следующие знания:
Таким образом мы получим уже не восемь, а четырнадцать исходных знаний и должны будем проанализировать, соответственно, четырнадцать реальных операций. Но оканчивается ли на этом процесс возможного разложения? Но что может гарантировать нам, что это разложение будет, наконец, полным и последним? В чём можно найти объективные критерии простоты тех или иных знаний и операций? Чтобы ответить на эти вопросы, мы должны изменить сам план и предмет исследования. Мы должны оставить в стороне вопрос о количестве реальных знаний и порождающих их операций в рассматриваемом краевом процессе и поставить целый ряд более общих вопросов методологического порядка. Мы должны выяснить принципы и основания подобного разложения, применимые при анализе разнообразных процессов мысли. А для этого мы должны исследовать возможные типы структур процессов мышления, содержащих не одно, а много реальных знаний. Начнём с некоторых соображений по рассматриваемому процессу. Уже самого поверхностного анализа перечисленных выше знаний достаточно, чтобы увидеть, что между ними существуют определённые зависимости. Например, знания (3), (4), (7.1) и (7.2) предполагают в качестве своего необходимого условия знание (1), а знания (5), (6), (7.3) и (7.5) предполагают знание (2). Знание (7), как мы уже сказали, предполагает в качестве своего условия, по крайней мере, восемь других знаний, причём внутри этой группы существует своя особая субординация. Знание (8) предполагает в качестве своего условия все перечисленные выше знания, включая и знание (7), и кроме того, Но такое положение дел даёт нам повод предположить, что существует также определённая зависимость и между операциями, порождающими эти знания. Ведь для того, чтобы определить EH как сторону треугольника, надо предварительно выделить сам этот треугольник или, чтобы путём Подобная же зависимость существует и между объектами, входящими в рассматриваемый процесс, хотя с выделением самих объектов и анализом их дело обстоит значительно сложнее. В соответствии с нашим пониманием структуры знания, каждое реальное знание должно иметь свой объект. На первый взгляд кажется, что их нетрудно определить: объект знания (1) — сам представленный на чертеже треугольник TEH, объект знания (2) — сам чертёж треугольника SLT, объекты знаний (3), (4), (5), (6) — соответствующие стороны этих треугольников, данные точно так же в чертежах, а объекты знаний (7.1), (7.2), (7.3) и (7.4) — «чертежные» углы; здесь все пока выглядит исключительно простым. Но когда мы переходим к знаниям (7.5), (7.6), (7), (8) или тем более привлекаем к рассмотрению продукт всего процесса — знание «EH:TH = LT:ST», — то положение осложняется. Продолжая линию, намеченную выше, мы должны были бы сказать, что их объектами являются «равенства определённых углов», «подобие треугольников TEH и SLT», «соответственность сторон этих треугольников» и, наконец, «равенство отношений EH к TH и LT к ST». Результат — совершенно неприемлемый для нас, так как объект знания отождествлен здесь с содержанием. И кроме того, возникает следующий вопрос: если объекты знания вводятся таким образом, то почему тогда мы разделили первую часть рассматриваемого краевого процесса на два движения и выделили соответственно два объекта, а не предположили сразу, что исходным объектом является сама «соответственность сторон подобных треугольников TEH и SLT», и в соответствии с этим не рассмотрели всю эту первую часть как одно знание? В этом случае мы имели бы в первой части краевого процесса (I) одно движение, и с этой точки зрении он ничем не отличался бы от процесса соотнесения. Вывод отсюда может быть только один: объекты знания нельзя выделять таким образом, их нужно выделять На первый взгляд довольно естественным кажется подход, когда, к примеру, в знаниях (7.5) и (7.6) в качестве объектов знаний рассматривают не равенство соответствующих углов, а сами эти углы, в знании (7) — не «подобие» треугольников, а сами эти треугольники, а в знании (8) — не «соответственность» четырёх сторон двух подобных треугольников, а сами эти четыре стороны. Тогда в соответствующих реальных знаниях оказывается не один объект, а два, три или четыре, и этот факт фиксируют, говоря, что указанные знания в отличие, к примеру, от знаний (1)–(6), (7.1)–(7.4), являются многообъектными — подход, получивший широкое распространение в логике с конца XIX столетия. Философскую основу этой линии составляют взгляды крайнего эмпиризма, в частности, той его разновидности, которая получила название «логического атомизма». Согласно этим взглядам, объектами исследования могут быть только единичные вещи и явления, в крайнем случае — их стороны, но ни в коем случае не отношения и не связи этих вещей, явлений или сторон. Когда представители этого подхода сталкиваются с отношениями и системами отношений, со связями и системами связей, то они рассматривают их как сопоставляемые друг с другом множества изолированных элементов или множества множеств таких элементов, тем самым исключая из рассмотрения главное и специфическое в этих объектах — сами отношения и связи, которые придают этим группам элементов качества целостности. В практике мышления, как повседневного, так и научного, мы постоянно имеем дело с отношениями, связями и системами отношений и связей как едиными целостными объектами: они выступают как то, что мы исследуем, как то, чем мы оперируем в познавательном действии, и, наконец, как то, к чему мы относим полученное знание. И подобно этому, объектами перечисленных выше «многообъектных» знаний на самом деле являются не линии, углы, а треугольники, и не группы из двух углов, четырёх линий или двух треугольников, а именно определённые взаимоотношения и системы линий, углов и треугольников, если понимать под «взаимоотношениями» и «системами» некие особые целостности или единства самих отношений и относящихся предметов (вещей). И эти целостности могут стать и становятся объектами исследования и объектами оперирования, в которых мы выделяем определённые свойства и к которым мы относим знаковые формы, фиксирующие эти свойства. Именно с этой точки зрения надо подходить к анализу знаний, к выделению их объектов, а подход, подобный подходу «эмпирического атомизма» может привести только к утере специфики этих знаний, определяемой спецификой их объектов, и закроет путь к исследованию порождающих их операций. Поэтому мы утверждаем, что и этот «многообъектный» подход так же не годен при анализе знаний и сложных процессов мысли, как и разбиравшийся выше, и делаем вывод, что необходимо выработать Здесь прежде всего оказывается, что нужны новые, дополнительные определения, характеризующие как объект вообще, так и, в особенности, логические типы и виды объектов. При анализе геометрии недостаточность нашего понятия объекта не чувствовалась потому, что там мы с самого начала имели определённые (с точки зрения своего материала) вещи и явления — определённые реальные предметы, чертежи, звуки, графические значки, и так далее — и рассматривали их сквозь призму схемы замещения, придавая каждому либо функциональную характеристику объекта, либо функциональную характеристику знака. Можно сказать, что мы как бы «накладывали» одну из ячеек отношения «объект — знак» на те или иные вещи и явления, заданные нам независимо от этого отношения. При таком подходе нам не нужны были никакие признаки объекта, кроме тех, которые заключены в самой схеме, тем более не нужна была исчерпывающая классификация видов и типов объектов. При анализе краевого процесса как процесса соотнесения у нас была в принципе такая же ситуация. Ведь в процессе соотнесения, по предположению, всего один объект, и существует единственное функциональное взаимоотношение — между этим объектом и знаковым выражением, фиксирующим его свойства. Поэтому единственными признаками, которые мы должны приписать объекту как элементу схемы, являются следующие: 1) он противостоит сложной знаковой ферме (или формальному знанию) и 2) на него направлена реальная познавательная операция, обеспечивающая переход от объекта к знаковой форме. Вопрос о том, что такое объект по своему материалу, а также о видах и типах объектов при таком подходе, естественно, не вставал. Но точно так же он не вставал и при приложении схемы процесса соотнесения к эмпирическим процессам мысли. Действительно, функциональное отношение «объект — формальное знание» остаётся одним и тем же независимо от природы или материала самого объекта. Поэтому объектом в процессе соотнесения может быть любая вещь и любой абстрактный предмет, выраженный в знаках. Важно только, чтобы между ним и знаковой формой существовало указанное функциональное взаимоотношение. А чтобы выяснить это, достаточно перечисленных выше признаков. Если пользоваться тем же сравнением, к которому мы прибегали выше, то можно сказать, что и здесь мы как бы «накладываем» схему процесса соотнесения на любые вещи и явления, и единственное, что нам нужно решать, так это вопрос, к чему относятся эти вещи и явления в том или ином эмпирическом процессе мышления — к объекту или к знаковой форме. Очевидно, что недостаточность понятия объекта не могла обнаружиться и здесь. Но когда мы переходим к анализу краевого процесса (I), эта недостаточность обнаруживается тотчас же — и прежде всего потому, что мы имеем дело с совершенно другой задачей исследования. Мы не имеем здесь готовой схемы, как раньше, которую надо наложить на те или иные эмпирически зафиксированные мыслительные явления в соответствии с функциональными определениями самой схемы, а должны ещё только выработать эту схему. При этом мы имеем дело со сложным процессом мышления, содержащим ряд реальных знаний и, следовательно, ряд объектов, и, чтобы выработать схему, адекватную этому процессу мысли, мы должны прежде всего определить, какое различие существует в функциях этих объектов и в каких отношениях друг с другом они могут находиться. Это и будет, фактически, необходимым определением объекта знания. Только после этого, после выработки таких общих схем возможных отношений между объектами мы сможем решать вопросы о количестве и характере объектов в тех или иных конкретных процессах мышления. Вопрос об объекте знания органически связан с целым рядом других принципиальных вопросов — о содержании и «предмете» знания, чувственном опыте и роли практики в познании, о значении языковых выражений, теории описания, и так далее, которые отчасти уже затрагивались нами в других местах. Здесь нам придётся вновь обращаться к полученным там решениям, а часто — брать вопросы с новой стороны. 20Проблема определения объекта знания имеет свою длинную историю. Не задаваясь целью рассмотреть её систематически, сделаем несколько замечаний по отдельным, важным на наш взгляд, моментам. В логике, построенной в соответствии с принципом параллелизма и изучающей в силу этого только знаковую форму, проблема объекта знания не могла встать в чистом и непосредственном виде. Но понимание структуры суждения как связи субъекта и предиката, как S — P подразумевало отношение свойства к объекту или знания о свойстве к знанию об объекте 33. Таким образом объект знания выступал в образе субъекта суждения, и на него в соответствии с принципом параллелизма переносилось всё то, что характеризовало субъект суждения S — P. Поэтому Аристотель двойственно характеризовал сам субъект: в логике — как элемент предложения, в риторике — как вещь (см., к примеру, [Серрюс 1948: 144]). Определение в обоих случаях оставалось одним и тем же: то, о чём говорят. Содержание знания по смыслу всей Аристотелевой концепции отождествлялось с тем, что выражено в предикате, и в этом плане противопоставлялось субъекту, а через него и объекту знания. Затруднения с интерпретацией субъекта суждения как непосредственного и единственного выражения объекта знания появлялись лишь в связи с анализом общих формальных знаний. Здесь ставились в первую очередь два вопроса:
Вопрос о возможности интерпретации структуры S — P как осуществляющей включение одного класса в другой возникал вторичным образом при сопоставлении пары суждений «А — B» и «B — C», в которых один и тот же термин B выступает один раз как предикат, а другой раз — как субъект. Весь процесс тогда выглядел бы как:
Другим аспектом этого же сопоставления могла быть мысль о связи двух свойств:
Но в силу определённого понимания структуры мира (род — «причина» вида) эти свойства длительное время не могли рассматриваться как рядоположные. Уже одно это делало невозможным предположение, что связь между этими свойствами может быть объектом особого рода. Независимо от того, каким было речевое выражение субъекта, всякое суждение рассматривалось как монообъектное, и это, фактически, предопределяло решение вопроса о видах объектов — безразлично к онтологическому смыслу все они с логической точки зрения были совершенно одинаковыми. Вместе с тем у Аристотеля были уже таблицы предикабилий и категорий, но это было связано не столько с логическим анализом, сколько с грамматическим и онтологическим (см. [Минто 1902: 75–84]). Стоики обсуждали проблему объекта знания в связи с теорией лекты (см. [Bochenski 1956: 126–131]), а в Средние века эта же проблема обсуждалась в связи с теориями второй интенции и суппозиции (там же, с. 176–179, 186–199), а также спором между реалистами, номиналистами и концептуалистами. В ХVII веке Лейбниц уже достаточно отчётливо осознает тот факт, что не всякое суждение (соответственно, предложение) может быть разложено на субъект и предикат. «Вот три человека», утверждение это, — замечает он, — не полагает рядом трёх существований; оно полагает сразу (en bloc) число таким образом, что в предложении не оказывается ни субъекта, ни атрибута» (см. [Серрюс 1948: 124]). Вся структура суждения выглядит в этом плане однородной; она вся напоминает предикат, а объект оказывается вытолкнутым из её сферы куда-то во вне. Возникает естественный вопрос о его существовании: где он и что он? Рассматривая сравнение двух линий (L) и M, Лейбниц отвечает на него: «Следует сказать, что это отношение находится вне субъектов и что, не будучи ни субстанцией, ни акциденцией, оно должно быть идеальной вещью, рассмотрение которой тем не менее не перестаёт быть полезным» (там же). В XIX веке этот подход получает интенсивное развитие в виде логики отношений. Прежде всего было обращено внимание на то, что в суждениях об отношениях, если исходить из их «естественного смысла», нет ничего похожего на связку «есть». Как выразился Ж. Лашелье, «связка в предложениях этого рода не имеет метафизического значения», то есть она не подразумевает отношения предиката к субъекту, знания о свойствах к объекту, — «она есть скорее аналог знаков, которыми пользуются в арифметике и в геометрии для выражения отношения чисел или отношений величин» (см. [Серрюс 1948: 123]). И это абсолютно правильно. Правда, в связи с этим тезисом многие представители логики отношений делали сразу две принципиальных ошибки.
Обсуждение вопроса о «сфере существования» объектов суждений об отношениях, привело к постановке вопроса о том, что представляют собой эти объекты, каковы их логические характеристики. При этом обнаружилось, что каждое такое суждение может иметь несколько различных объектов. «В действительности под этим предикатом LrM разумеют несколько субъектов, каждый из которых будет определён посредством установки на значение», — пишет Ш. Серрюс (там же, с. 146). И в другом месте: «Лейбниц научил нас интерпретировать во всех возможных смыслах одно и то же сравнение двух прямых (L) и M. Таким образом, вот ещё несколько возможных субъектов для одного и того же предиката. Точно так же a = b может иметь в качестве субъекта, смотря по установке, то a и b, то a, то b, то, наконец (Лейбниц обошел вниманием последний случай), — само равенство» (там же, с. 158–159). Но следствием такой постановки вопроса об объекте знания явилась новая постановка вопросе и о содержании. Эти формулы 34 крайне интересны, ибо в них впервые, благодаря повторению знака А, появляется изображение объекта в его отличии от содержания. Но вместе с тем, в этих формулах нет самого главного: не подчёркивается принципиальная разнородность этих двух элементов акта мысли — объекта и знаков, фиксирующих его свойства-стороны. Изображения, введённые Джевонсом, остались ориентированными исключительно на сферу знаков и поэтому внешне сохранили свою связь с традицией. Но именно поэтому не был понят действительный смысл этих изображений. Позднейшие логики отвергли их — в прямом несоответствии со структурой и нормами языка они дважды повторяют знак А, а вместе с тем и скрывающееся за ним содержание. Общим следствием всей этой эволюции точек зрения было заострение вопроса об отношении формы знания к объекту, или, говоря традиционным языком, — суждения и предложения к объекту. Направленность высказывания на объект, а вместе с тем и сам объект являются необходимыми элементами мысли — таков был наиболее важный вывод. Но логика, стремясь соблюсти точность и строгость своего анализа, вынуждена была игнорировать этот тезис и искать все возможные оправдания для этого. «Значит ли это, что субъект исключается из мысли? Как раз наоборот; из этих наблюдений следует, что он составляет постоянный фон суждения — как в том случае, когда он выражен, так и в том, когда он подразумевается. Он есть предмет мысли и область, в которой я утвердился с тем, чтобы судить … и всё же он остаётся вне логической сферы — если под ней следует разуметь замкнутую область, включающую в себя лишь связи суждений и умозаключений и содержащую только технику мысли» [Серрюс 1948: 145]. Ниже: «… апофантические значения (les valeurs apophantiques) исключены из научного изложения» (там же, с. 146). «Изолированный предмет, если угодно, есть и нечто убогое; он похож на тело без души — если его отделить от субъекта. При сравнении его с богатством апофантической структуры он кажется бедным. Однако, в конечном счёте, это — описание некоего порядка и выражение некоей теоретичности, а этим отнюдь не следует в такой мере пренебрегать… Во всяком случае логика может рассматривать в суждении только это, а именно — его теоретическое строение. Поэтому мы отказываемся принять, что новейшая доктрина уступает доктрине Аристотеля, так как она составляет лишь род Органона, неполного и абстрактного. Напротив, она есть сама логика, орудие мысли, но не мысль, так как всеми способами необходимо добиться, чтобы содержание осуществлялось в формах теоретичности, которую эта доктрина выражает» (там же, с. 148–149). Казалось бы вывод должен был быть противоположным. Если объект есть обязательный элемент мысли, и в то же время он существует вне структуры самого предложения, вне структуры знаковой формы, то из этого следует только один вывод, что изображение акта мысли, а вместе с тем и знания нужно дополнить ещё одним графическим знаком, изображающим этот объект как элемент мысли. И этот знак должен быть поставлен в определённую связь со знаками, изображающими структуру предложения, связь, подразумевающую и обозначающую действительную связь между этими элементами мысли. Но подавляющее большинство логиков побоялись идти на столь резкий разрыв с традицией и сделали противоположный вывод: объект, несмотря на то, что он является обязательным элементом акта мысли, не входит в сферу логического анализа и не нуждается поэтому в особых изображениях. На этот путь становится, в частности, Б. Рассел и, необходимо, — все «формалисты» в логике. Вместе с тем в этой связи для них теряет свою актуальность вопрос об объекте и типах объектов. Он вновь встаёт во весь рост в связи с обнаружением различия в способах связи элементов суждения, как вопрос о различии мыслимых содержаний и приводит к теории типов Рассела. Резюмируя всё изложенное, можно сказать, что в собственно логике вопрос об отношении знаковой формы к объектам всегда под тем или иным предлогом элиминировался. Представители теории познания и теоретико-познавательной логики — английские гегельянцы Ф. Г. Брэдли и Б. Бозанкет, Э. Гуссерль и психологи Вюрцбургской школы, имманент В. Шуппе и русский интуитивист Н. Лосский — подходят к проблеме иначе: для них вопрос об отношении формы знания к объекту, а вместе с тем и вопрос о типах объектов имеет первостепенное значение, однако и никому из них не удаётся выработать строгий метод исследования и изображения этого отношения. Позиция логики отношений, дающая бесспорный положительный результат в плане выделения и обособления объекта создаёт вместе с тем новые затруднения в различении объекта и содержания знания. При традиционном понимании схемы S — P это различие было исключительно простым: S есть субъект и представитель объекта, P — предикат и представитель содержания, то есть вычленяемой в объекте стороны. Но если вся структура суждения (или предложения), как это принимает логика отношений, есть не что иное, как предикат, то вопрос о показателях различия между объектом и содержанием знания встаёт вновь во всей остроте. Необходимость их различения становится очевидной в тех случаях, когда объект имеет реальное представительство в мысли в форме знаков принципиально иного рода, нежели знаки предикации. «Так как предикат и субъект независимы, вопрос становится уже не об их «логическом» отношении. Их следует поместить один против другого — подобно тому, как в двух столбцах реестра записывают счетные операции против названия дела, к которому они относятся, — пишет Ш. Серрюс. — В нашем реестре мы можем надеяться привести к соответствию вещи настолько разнородные, как, например, фигура (объект) и уравнение (предикат)» [Серрюс 1948: 154]. Но как быть в тех случаях, когда такого представительства нет, когда объект лишь подразумевается под формой однородного (с точки зрения типа знаков) предиката и подразумевается как таковой, в своём отличии от содержания, фиксируемого этим же предикатом? Г. Фреге выходит из положения, привлекая к сравнению такие формы, как «Утренняя звезда» и «Вечерняя звезда», «Победитель при Аустерлице» и «Побеждённый при Ватерлоо»: тождество их значений, говорит он, даёт нам предмет, а различие — смысл (или содержание). Но такое умозаключение само возможно только в том случае, если мы знаем, что и утренняя, и вечерняя звезда — это одна и та же планета Венера, а победитель при Аустерлице и побеждённый при Ватерлоо — это Наполеон, то есть если мы знаем, что в каждой паре этих выражений подразумевается один и тот же объект. Именно поэтому Г. Фреге так и не удаётся решить вопрос о значении равенства «а = в» [Frege 1892]. Ш. Серрюс говорит более удачно: «В других случаях алгебраический предикат и геометрический предикат относят к одному и тому же субъекту (например, способ получения фигуры и способ анализа, которые оба выражают мысль о кривых второго порядка». Но опять необходимо сравнение двух разнородных предикатов, и объект, всё равно, остаётся по существу не выявленным и не зафиксированным («оба выражают мысль о кривых второго порядка»). А как быть в тех случаях — а их подавляющее большинство — когда дана одна лишь знаковая форма?» Когда вся цель разрешения проблемы состоит в определении x, x и является субъектом заключения:
Пишет Ш. Серрюс. — То же самое справедливо относительно всей дедукции в целом, ибо не будет ничего странного в том, что нам говорят здесь о субъекте всего рассуждения, или всего умозаключения» (там же, с. 147). Но это не решение вопроса, которое может быть дано лишь в обобщённой форме. Совершенно очевидно, что оно не может быть применено к таким простым суждениям как именные, имперсоналии, и так далее. Да и сам Серрюс отчётливо чувствует это; сразу же после приведённого выше места он пишет: «И всё же в перестановках, которых требует разрешение проблемы, x оказывается введённым в систему предиката в качестве термина, с которым мы, однако, не связываем специального значения. Он даже не всегда занимает первое место в уравнениях или неравенствах (чего, впрочем, как мы уже знаем, было бы недостаточно для сообщения ему достоинства субъекта)». И немного ниже: «Длинные цепи Декарта являются рядами предикатов, и если мы примем эти самые невыраженные субъекты всех утверждений, необходимо допустить, что они вводятся в виде предикативной формы». Именно отсюда следует заключительный тезис Серрюса (мы разбирали его выше), что объект, несмотря на всё своё значение для мысли, остаётся вне сферы логики. И он закономерен, так как логика отношений, подобно классической Аристотелевой логике не знает пути, каким можно было бы разделить объект и содержание и ввести то и другое в схемы логики. В приведённой выше алгебраической формуле не случайно стоит знак индивидуального тождества. Это вытекает из смысла и назначения акта познания в понимании Серрюса — дать интенцию на объект. Но ведь вместе с тем этот знак символизирует тождество объекта и содержания знания. И если мы будем не характеризовать x через посредство выражения:
Предполагая, что это лишь одна его сторона, а будем вводить и определять x путём отождествления его с этим выражением, то x приобретет отнюдь не индивидуальное, а общее значение, не имеющее, казалось бы, никакой интенции на индивидуальный объект. Но будет ли это означать, что у этого выражения нет объекта? Таким образом Ш. Серрюс приходит к естественному выводу, что объект определяется установкой на значение, и эта установка весьма произвольна, пока мы имеем дело с отдельным выражением, взятым вне контекста того процесса мышления, в котором оно было получено или используется, это действительно так. Выражение «а = b» может быть отнесено по меньшей мере к четырём объектам: 1) a, 2) b, 3) ab— (черта внизу означает, что а и b берутся как совместно существующие) и 4) аRb. Точно так же и атрибутивное выражение (А) — (В), если брать его изолированно и рассматривать интенсиональные значения в качестве объективных, может иметь по меньшей мере шесть объектов: 1) А как единичная вещь, 2) А как класс, 3) А как свойство, 4) АВ— как совместность свойств, 5) АrВ как отношение классов, 6) А — В как связь свойств. Если же мы берём это выражение в контексте определённого процесса мысли, то такое произвольное определение объекта уже неуместно. В контексте определённого процесса мышления у этого выражения может быть только один, строго определённый объект, который нужно уметь выделить. И этот объект в каждом таком процессе мышления резко и определённо противостоит содержанию знания. Мы говорим «противостоит». И это действительно так, ибо в этом противопоставлении собственно и заключается смысл и значение всякого целостного акта мысли: как и всякий другой акт познания он направлен на выявление (получение) нового содержания. Но как отличить, отделить их друг от друга для каждого выражения в конкретных случаях? Логика отношений не даёт ответа на этот вопрос. Логический позитивизм пытался решить проблему объекта и содержания знания, во-первых, с позиций радикального сенсуалистического эмпиризма, во-вторых, (по линии собственно логики) с позиций крайне зкстенсионалистской точки зрения. Характерными для первого этапа в обсуждении проблемы являются статьи Р. Карнапа «Scheinprobleme in der Philosophie; das Fremdpsychische und der Realismusstreit» и М. Шлика «Positivimus und Realismus». Эволюция взглядов логического позитивизма на протяжении 30 лет завершилась отказом от обоих принципов. Это нашло отчётливое выражение в работах К. Поппера, К. Гемпеля, в последней работе В. Крафта [Kraft 1960] и в работах самого Р. Карнапа (cм. [Карнап 1959]). Для математической логики в целом способы определения объекта и содержания знания — а к ним приходится постоянно обращаться в связи с потребностями именно логики — составляют в настоящее время загадку. Это проявилось, в частности, в продолжающейся уже более 10 лет дискуссии по поводу универсалий и абстрактных предметов [Bochenski 1957; Church 1966, 1958; Goodmen 1955, 1956; Linsky 1952; Pap 1957;Quine 1939, 1943, 1947, 1948, 1951, 1951 b; Ryle 1949; Wilson 1953]. 21Таким образом, можно сказать, что существующие в настоящее время подходы к определению объекта и содержания знания не могут решить тех логико-гносеологических проблем и вопросов, которые были поставлены и обсуждались уже в прошлом. Но перед нами, в контексте проводимого анализа, встают кроме того новые вопросы, и проблема поворачивается такими сторонами, которые раньше не обнаруживались. И эти стороны, на наш взгляд, являются собственно логическими. Суть их в самом общем виде может быть выражена следующим образом: если сложное рассуждение (направленное на решение определённой задачи) разлагается на отдельные операции и содержит, соответственно, ряд знаний, то оно должно содержать также и ряд объектов (в предельном случае — как раз по числу этих знаний). Вместе с тем это рассуждение, если оно является одним цельным образованием, должно содержать всего один объект, к которому относится вопрос задачи. Преодолеть эту антиномию можно только одним способом — предположив, что объекты частичных знаний и операции находятся в определённых отношениях и связях друг с другом и образуют благодаря этому сложную структуру, которая и является объектом всего мыслительного процесса в целом. Но такой вывод выдвигает на передний план вопрос о видах этих объектов (с точки зрения целого) и их взаимоотношений. В частности, исключительно принципиальное значение имеет вопрос общего порядке: можно ли все эти многочисленные и разнообразные объекты рассматривать как лежащие наряду друг с другом, как бы на одной линии, или же между ними существуют При этом надо помнить, что речь идёт совсем не об объектах как таковых, то есть не о реальных вещах, а об «объектах знания». Мы занимаемся здесь исследованием не объектов того или иного типа, а исследованием процесса мышления, и объекты знаний должны интересовать нас именно в этом плане. Иначе говоря, нас должны интересовать не просто объективные взаимоотношения и связи между объектами знания в онтологическом плане, а те отношения между ними, которые устанавливаются процессом мышления, то есть отношения между ними как объектами разных знаний, включённых в процесс получения другого знания. Но это означает, что вопрос об отношениях объектов частичных знаний друг к другу и к объекту целого сливается с вопросом об отношениях друг к другу самих знаний и должен рассматриваться именно в контексте последнего. Иначе: решить вопрос о взаимоотношении объектов знаний в сложном процессе мышления — это и значит решить вопрос о взаимоотношении соответствующих знаний. Таким образом, здесь не может быть никакой чистой онтологии, а может быть только логика и, соответственно, логическая онтология. Тогда вопрос, сформулированный выше, приобретает вид: можно ли все многочисленные и разнообразные знания и операции, входящие в анализируемый сложный процесс, рассматривать как лежащие наряду друг с другом, как бы на одной линии, или же между ними существуют сложные иерархические отношения — и если да, то какие? Но решить этот вопрос — это и значит решить вопрос о том, как относятся друг к другу объекты этих знаний. С другой стороны, от решения этого вопроса, хотя бы в общем виде, в свою очередь зависит, что именно мы будем называть объектами и, соответственно, выделять в качестве объектов в конкретных эмпирически заданных процессах. Поясним это на примерах. Предположим, что мы анализируем высказывание о взаимоотношении двух треугольников X и Y. Может ли быть названо это взаимоотношение объектом? Существует ли оно как объект? Мы его, конечно, объективируем, но достаточно ли констатации одного этого факта, чтобы уже можно было говорить об объектах? И не исчезнет ли у нас тогда всякое различие между объектом и содержанием знания? И, наконец, даже если мы признаем, что взаимоотношение треугольников есть объект, то можно ли его рассматривать как объект того же типа и слоя, какими являются сами треугольники X и Y. Или вот другой пример — стороны треугольников в высказывании «В подобных треугольниках отношения соответственных сторон равны». Можно ли рассматривать их как объекты вообще и как объекты, лежащие наряду с такими объектами, как сами треугольники, в частности? Если бы мы рассматривали по отдельности такие знания, как «Вот сторона а треугольника X», «Вот треугольник X», «Вот отношение между сторонами a и b треугольника X», и так далее, то мы могли бы это сделать, то есть могли бы рассматривать их не только как объекты, но и как объекты, лежащие как бы на одной линии. Действительно, в каждом из этих знаний, если брать его само по себе, между объектом и знаковой формой, фиксирующей определённое его свойство, такое же отношение, как и в другом, и нет собственно ничего, что мешало бы нам расположить их рядом друг с другом, на одной линии и так же сопоставлять между собой. Но когда мы берём эти знания и соответствующие им объекты в контексте и в структуре одного процесса мышления, то мы уже не можем так подходить, а должны выяснять их взаимоотношения с точки зрения самого процесса мышления. К этой же проблеме можно подойти и с другой стороны. Ведь, начиная анализ строения выделенного нами краевого процесса (I), мы отвлеклись от того обстоятельства, что действительным объектом всего процесса решения задачи в целом являются реальные расстояния «Земля — Луна», «Земля — Солнце», и предположили, что краевой процесс имеет дело уже только с чертежами. А если мы теперь вспомним и учтём это обстоятельство, то перед нами сразу же встанет вопрос: можем ли мы рассматривать одновременно в качестве объектов процесса мышления реальные расстояния «Земля — Луна», «Земля — Солнце» и их изображения в чертежах и если да, то как мы должны располагать их — на одном уровне как объекты одного порядка или же на разных уровнях в соответствии с определённой иерархией? Для знаний, входящих в один процесс мышления, проблема встаёт аналогичным образом. Только приступив к анализу краевого процесса (I), мы выделили по меньшей мере четырнадцать различных знаний и встали в тупик перед вопросом: можно ли их рассматривать как однородные, лежащие наряду друг с другом, или между ними существует своя сложная иерархия отношений? Интуитивные соображения непосредственно по этому процессу мысли, а также опыт анализа процессов мышления в геометрии склоняют скорее к последнему. Действительно, трудно предположить, чтобы знание, устанавливающее определённую характеристику — соотношение между отношениями EH к TH и LT к ST, лежало наряду со знаниями о сторонах — элементах этих отношений. Но даже если эти интуитивные соображения верны, они ничего не говорят о всех этих слоях и уровнях, об отношениях между ними и их типологической структуре. Но раз не выяснена структура этих знаний и их взаимосвязи, остаётся совершенно неясным, в каких символических структурах можно и нужно их изображать, как фиксировать эти иерархические взаимоотношения. Проведённый выше анализ геометрического материала подсказывает нам ответ на вопрос относительно общих типов знания и возможных взаимоотношений между ними. И прежде всего он даёт возможность наметить три основных группы процессов мысли, которые могут составлять элементы сложных процессов. Для характеристики процессов первой группы можно взять мыслительные операции, которые мы осуществляем, отвечая на вопросы: «Сколько предметов на этом столе?», «Какова длина этого стола?», «Равны ли по длине эти две верёвки?» и так далее. Во всех этих случаях исследуемый объект и вопрос относительно него заданы таким образом, что существует одна познавательная операция — счёт, измерение, наложение, и так далее — решающая задачу. Эта познавательная операция направлена непосредственно на объекты (и сама представляет собой особую модификацию замещения одних объектов другими), она выделяет в объектах определённое содержание и может рассматриваться как лежащая в одной плоскости с самими объектами. Результат этой познавательной операции выражается в определённой знаковой форме (цифры, слова «равно» и «не равно», и так далее), которые находятся уже как бы в другой плоскости по отношению к объектам и самой операции: операция как бы исчезает в этом языковом выражении, последнее замещает операцию и выделенное посредством неё содержание. Наглядно-схематически описанный процесс мысли может быть изображён в формуле, которую мы уже чертили выше:
Где, напомним, Х — объект, D — непосредственно-практическая часть мыслительной операции, (А) — знаковая формула, а вертикальные стрелки и ¯ изображают переход от объективного содержания, выявленного в плоскости объектов — Х D, к знаковой форме, лежащей уже в другой, более «высокой» плоскости, и назад, от знаковой формы к объекту Х. С точки зрения этой схемы мы можем несколько уточнить то, что говорили выше относительно самой операции: она соединяет плоскость объектов и плоскость знаковой формы. Перейдём ко второй группе процессов. В ряде случаев объект и вопрос относительно него бывают заданы таким образом, что не существует одной познавательной операции, посредством которой можно было бы непосредственно решить задачу. Например, нельзя непосредственно сопоставить по длине два непередвигаемых объекта, расположенных в разных местах, нельзя измерить длину кривой линии прямолинейным эталоном, и так далее. В этих случаях задачу решают, преобразуя исходный объект Х к такому виду Y или замещая объект Х другим объектом Y, таким, что к Y может быть применена какая-либо операция типа и ¯D, дающая знание, которое может рассматриваться как ответ на вопрос относительно Х. При этом между Х и Y устанавливается особое отношение замещения, которое получило название отношения эквивалентности (см. по этому поводу [Ладенко 1958]). Именно таким образом, к примеру, решал задачу Галилей, когда он приступил к изучению свободного падения тел, но не мог достаточно точно измерять время такого движения и заместил его движением шарика, скатывающегося по наклонной плоскости. При этом он должен был специально обосновать, что оба этих движения, как замещаемое, так и замещающее, подчиняются одному и тому же объективному закону (подробнее это разработано в статье [Щедровицкий 1958 a]). Наглядно-схематически описанный процесс решения задачи может быть изображен формулой:
Или, наконец, формулой:
Знак = (читай «эквивалентно») обозначает здесь замещение объекта Х другим объектом Y, а g — любой сложный процесс, обеспечивающий это замещение. Для процессов этой группы характерно то, что как операция замещения, так и непосредственно-практическая часть познавательной операции D осуществляются в плоскости объектов, а языковое выражение (А), фиксирующее содержание, выделенное посредством D в объекте Y относится к объекту Х. В качестве примера процессов третьей группы можно взять любой процесс соотнесения. Необходимым условием их являются предварительная выработка и использование в ходе решения определённой задачи сложной знаковой фермы (иначе — формального знания), которая в простейших случаях представляет собой отдельное выражение вида «Все (В) суть (А)» или систему таких выражений. Наглядно-схематически эти процессы мысли мы изображаем в формулах:
Где (В) есть знаковое выражение, фиксирующее результат применения D к объекту Х, а l изображает «формальные преобразования» (осуществляемые в соответствии со связями и правилами формальной знаковой системы), приводящие выражения вида (В), (С), (D)… к виду (А), которое может рассматриваться как ответ на исходный вопрос относительно объекта Х. Другими примерами процессов этой же группы будут: сложение нескольких чисел, дающее ответ на вопрос о количестве объектов в совокупности, части которой находятся в разных местах; вычисление длины окружности на основании формулы L=2pR, после того как измеряна длина радиуса этой окружности; использование уравнения химической реакции для ответа на вопрос, какие вещества получатся, если мы приведём во взаимодействие другие определённые вещества, и так далее. Для всех процессов этой группы характерно, что большая часть составляющей их деятельности лежит в плоскости знаковой формы (есть, следовательно, деятельность не с объектами, а со знаковыми выражениями) и имеет чисто формальный характер. Специально следует отметить, что процессы каждой из этих групп могут комбинироваться с другими (по сути вторая и третья схемы уже содержат внутри себя первую, но вторая и третья также могут быть объединены); в каждой из них заключены широкие возможности для присоединения новых элементов как по краям, так и внутри схемы. В общем случае сложные процессы мысли имеют,
Или кольцеобразные сочленения вида:
Первая схема, к примеру, может служить для изображения процесса решения геометрической задачи, при котором исходная замещающая фигура включается в более сложную фигуру и получает в связи с этим новые определения, позволяющие в соответствии с уже имеющейся сложной знаковой формой приписать этой фигуре (а вместе с тем и объекту Х) новое свойство; (b) в этой схеме изображает геометрическую фигуру, замещающую на основе операции D исходный объект, (a) — эта же фигура, получившая новое определение, = — знак эквивалентного замещения, D¢ — операция, выделяющая в (a) свойство, которое фиксируется в знаке (В), а (А) — знаковое выражение свойства, которое в соответствии с формальным знанием (В) (А) приписывается (a), затем (b) и, наконец, самому Х. Специфику сложных процессов мысли в каждом случае образуют, во-первых, сами составляющие операции, их содержание и строение, а во-вторых, порядок и способы комбинирования этих составляющих. Большую роль играет при этом соотношение содержательных и формальных операций в этих процессах. Важно также отметить, что часто повторяющиеся комбинации элементарных процессов закрепляются в виде определённых строго фиксированных приемов; в качестве примера можно указать на приём среднего пропорционального в геометрии. В частности, этим воспользовался Аристарх Самосский, когда проводил линию TG под углом 22½° к TE, чтобы определить отношение IE к DE. Важно специально отметить — и это отчётливо видно на самих схемах — что на определённых отрезках подобных сложных мыслительных процессов знаковые формы, замещающие исходный объект, могут рассматриваться как объекты особого рода, и тогда к ним применяется особая деятельность, напоминающая те содержательные преобразования собственно объектов, которые мы рассматривали выше в качестве второго случая. Многочисленные примеры этого мы видели при разборе мышления в геометрии. Это обстоятельство объясняет и ту относительность понятий объекта и содержания знания, с которой мы постоянно сталкивались выше. Действительно, пусть Х наш исходный объект. Операция D — выделяет в нём определённую сторону. Мы получаем содержание, которое в своём логическом анализе выражаем знаками Х D. Это содержание в ходе образования знания обозначается, фиксируется знаком (b). Благодаря этому оно опредмечивается, овеществляется, само становится особым объектом, с которым мы можем действовать, действуя определённым образом со знаком. Так появляются объекты особого рода. Это не просто материал знака — взятый таким образом, он может быть объектом, но это будет уже нечто совсем другое. Это — содержание в чистом виде, как бы оторванное от Х (а оно действительно отрывается, поскольку вместо Х появляются Y, Z и так далее), выступает в виде самостоятельного объекта. Но оно может сделать это лишь постольку, поскольку оно выражено, обозначено, зафиксировано в знаке, который собственно и выступает как вещная оболочка этого содержания, как плоть того, сущностью которого является это содержание. Но это содержание, даже зафиксированное в знаке, не будет ещё объектом до тех пор, пока к нему не будет применена определённая деятельность. И эта деятельность, деятельность особого вида, возникает. Она направлена непосредственно на материал знаков, и это обстоятельство накладывает на неё определённый отпечаток, то есть определяет какую-то её сторону, но в существе своём она направлена именно на содержание, это есть оперирование с содержанием, и основные законы её поэтому определяются именно содержанием. Деятельность эта такова, что в содержании Х , взятом как объект (b), оно выделяет новое содержание (b) D¢, которое в свою очередь выражается, обозначается, фиксируется в знаке. Если говорить о смысле этого повторного выделения содержания, то оно должно заключаться, Во всяком случае, приведённые выше схемы возможного строения сложных процессов мышления объясняют довольно удачно динамику объекта и содержания — их относительность и переходы друг в друга. Они показывают, как может сложиться сложная иерархия деятельностей, выделяющих в объекте содержание, переводящих содержание в объект, снова выделяющих уже в этом новом объекте содержание и снова переводящих его в объект и так далее. Но, Другой интересный момент, отчётливо выступающий при анализе приведённых выше схем процессов мышления, касается функциональных определений объекта. В процессе соотнесения, который служит нам первой моделью краевого процесса, был всего один объект (хотя теперь, обогащённые всем проделанным анализом, мы могли бы найти в нём возможно и большее их число); он совмещал в себе три функциональных определения: во-первых, был тем, что исследуется и познается в данном процессе мысли; во-вторых, был тем, на что непосредственно направлена практическая содержательная операция; наконец, в-третьих, — тем, к чему в конце процесса мысли относится знаковое выражение, оставшееся после исключения промежуточных членов в общем формальном знании. Таким образом, объект в процессе соотнесения был объектом исследования, объектом содержательного оперирования и объектом отнесения. В процессах мышления такого типа, как изображённые на новых схемах, эти три определения уже расходятся. Объект исследования задаётся исходным вопросом задачи; поэтому в каждом конкретном процессе мысли мы можем считать его неизменным и полагать, что он легко определяется. На первом этапе исследования этот объект может быть вместе с тем и объектом оперирования, но затем в сложных процессах мысли объектами оперирования могут становиться все новые и новые знаковые формы. В каждом частичном процессе, который мы можем выделить как относительно самостоятельный, они будут вместе с тем и объектами исследования, но в контексте всего сложного исходного процесса мысли эти определения к ним уже неприменимы. Эти факты выдвигают на передний план новое обстоятельство, а именно проблему отнесения. В процессах соотнесения мы рассматривали заключительный акт отнесения как направленный на тот же самый, единственный объект, с которого начиналось движение. Это давало нам возможность рассматривать само это отнесение и его направленность как простое следствие исходного движения от объекта и фактически элиминировать специальный анализ самого отнесения и определяющих его факторов. В рассматриваемых теперь сложных процессах последнее языковое выражение непосредственно соответствует иному объекту, нежели тому, с которого началось движение, оно, следовательно, не может рассматриваться как простое следствие исходного движения, и поэтому исследование его направленности и функции в сложном процессе мышления выделяется на передний план и становится специальной задачей. Особую проблему, в частности, ставит вопрос: существует ли своё частное отнесение в частичных процессах мысли, входящих в более сложный процесс, или в таких процессах есть только одно общее завершающее отнесение к исходному объекту исследования? Нетрудно заметить, что этот вопрос означает по существу следующее: какая из двух приведённых выше формул — первая, «раскрытая», или вторая, «циклическая» — точнее передаёт строение мысли — или, может быть, существуют процессы, соответствующие как одной, так и другой? И если в частичных процессах-элементах существуют свои локальные отнесения, то в каком отношении стоят они к общему, заключительному? К этой же группе вопросов принадлежит вопрос о целостности процесса мысли; в частности, в свете новых моментов требует дополнительного анализа выдвинутая выше идея, что признаком целостности служит цикличность процесса. Если верна и вторая схема, то эта идея будет, очевидно, ложной. Прежде чем перейти к новым вопросам, подведём некоторые итоги нашего анализа. Столкнувшись с задачей выделить объекты знаний в сложном процессе мысли, мы вынуждены были поставить вопрос о возможных типах этих объектов, который затем слился с вопросом о возможных типах знаний в этих процессах. Решение последнего вопроса, в свою очередь, оказалось зависимым от решения вопроса о возможных взаимоотношениях знаний и их объектов внутри сложных процессов мысли (ибо в этом, как выяснилось, и заключена суть вопроса о типах). Таким образом здесь переплелись два вопроса, которые раньше казались нам раздельными: 1) о возможных типах знаний и объектов знаний и 2) о слоях или уровнях расположения этих знаний, их объектов и соответствующих мыслительных действий в контексте сложных процессов мышления. Решение первого оказалось зависимым от решения второго, а ответ на второй, в свою очередь, оказался связанным с анализом строения тех операций мышления, посредством которых эти знания получаются из других. Таким образом и здесь — мы повторим это ещё раз — нет никакой чистой онтологии, а есть особый логический анализ, включающий в себя в качестве подчинённых онтологические моменты. Этот вывод крайне важен для оценки исторических подходов к проблеме. Рассматривая их, необходимо разделять вопросы, касающиеся знаний, и вопросы относительно объектов этих знаний, так как обсуждение их шло принципиально различным образом: всё, что касалось знаний, рассматривалось в гносеологии и логике, а всё, что касалось объектов знания, по преимуществу в онтологии (или метафизике). Исключительно интересные постановки вопроса об объектах различных знаний и их статусе имеются у Аристотеля в «Метафизике». Примечательно также, что число, выражавшее отношение, во времена Евклида рассматривалось вообще не как число — во всяком случае, как сущность совершенно другого рода, нежели обычные числа, полученные из пересчёта [Начала Евклида 1948: Примечания]. В какой мере ХХ век стоит позади в тонкости анализа, можно видеть хотя бы на примере рассуждений Ш. Серрюса. «Мы рассматриваем мысли об объектах, поставленные лицом к лицу с предикативными построениями, — пишет он. — Мы исследуем субъекты суждений восприятия, повествовательных суждений, а также субъекты научных суждений. Мы должны будем остановиться на определениях — определениях имён и определениях вещей. Далее мы рассмотрим — в разделе о возможных субъектах — аристотелевский род и математическое множество, перебрав таким образом (курсив мой. — Прим. авт.) — по крайней мере мы так думаем — существенные формы субъектов, определённые посредством их отношений к их предикатам» [Серрюс 1948: 154]. Специального разбора требуют гносеологические концепции объекта А. Мейнонга и Э. Гуссерля. Б. Рассел пришёл к различению типов объектов от собственно логических проблем. Но никто из них так, Но до тех пор, пока не решена эта задача, невозможен анализ самого главного в сложном процессе мысли — переходов от одних частных объектов к другим. У нас не оказывается никакого принципа, который помог бы нам за совершенно хаотическим переплетением многозначных форм высказываний увидеть закономерный ход мысли. Этот вывод ставит перед нами задачу первоочередной важности: рассмотреть способы содержательного оперирования с объектами разного типа (и, следовательно, разных слоёв мышления), разложение объектов в соответствии с этими способами деятельности и возможности замены одних способов деятельности другими при соответствующей замене формы обозначения исходных содержаний. Богатый материал для такого анализа даёт, 22Мы рассмотрели два из поставленных выше вопросов и наметили примерные пути их разрешения. Но остаётся ещё третий вопрос: сохраняет ли анализируемый процесс мысли своё Т-образное строение при разложении на двухплоскостные единицы, или, иными словами, раскладывается ли он при них по-прежнему на основной и краевые процессы? Обсудим его. Предыдущий анализ привёл нас к выводу, что рассматриваемый процесс мысли состоит из шести как бы приложенных друг к другу краевых процессов. То, что объединяет, связывает их в одно целое, есть так называемая «основная линия» процесса. Но в этой основной линии не оказалось собственно процесса мысли. Это лишь цепь формальных математических соотношений, в соответствии с которой после того, как она получена, совершаются формальные преобразования и формальный «перенос» численного значения. Каждое из математических соотношений, как мы выяснили, должно иметь своё основание в определённых взаимосвязях элементов чертежа и соответственно в определённые мыслительных движениях, во-первых, по чертежу, а во-вторых, от чертежа к формальным словесно-алгебраическим или словесно-арифметическим соотношениям. В этих движениях, предположили мы, и заключено собственно мыслительное движение. Наглядно-символически итог нашего анализа можно изобразить в такой схеме:
Где верхние вертикальные линии выражают формальные соотношения, а нижние — содержательное движение в чертежах. Но этот итог является во многом парадоксальным. Ведь, если соотношения, лежащие в верхней плоскости, связаны, а их основания, изображённые внизу, не связаны, то основание этой связи должно быть заключено либо в самих этих соотношениях, либо ещё в каком-то третьем образовании, являющемся необходимым элементом процесса мысли, но лежащем в Кроме того, при таком понимании процесса мысли, которое изображено на предыдущей схеме, исчезает целостность рассматриваемого процесса мысли именно как движения. Продукты его связаны, а сам он представляет разрозненную «кучу»; мы теряем целостность самого движения и те факторы, которые определяют переходы от одних взаимосвязей элементов чертежа к другим. Но если мы признаем наличие такой связи в «нижней плоскости» оснований, то мы, по существу, зачеркнем весь принцип разложения процесса мысли на основную и краевые линии. Весь процесс будет представлять собой пусть внутри очень сложное, но с внешней стороны цельное единонаправленное движение. Обращение к эмпирическому материалу текста убеждает, что такая целостность и связь процесса мысли должны быть. Возьмём хотя бы первый краевой процесс: «Из подобия треугольников SLT и TEH следует…». Но откуда берутся подобные треугольники, или, точнее, как устанавливается подобие этих треугольников? Оказывается, что треугольник TEH с самого начала строится так, чтобы быть подобным треугольнику SLT. Чем это определяется? И мы можем предположить лишь один ответ: во-первых, в Правда, здесь мы встаем перед исключительно важной проблемой: что представляет собой это движение в «плане решения» задачи, из чего оно возникает и какие специальные символические средства предполагает? Но это уже другая, побочная проблема, а сейчас нам важно подчеркнуть саму зависимость построения подобного треугольника от других «шагов» процесса, в том числе «шагов» в чертежах. Во втором краевом процессе мы также обнаруживаем весьма характерную вещь. Предложение «Так как FE TH» имеет своим основанием чисто наглядные соображения и функциональные определения: «TH — наклонная, TE — перпендикуляр» или «TH — гипотенуза, TE — катет». Точно так же — и предложение «FE = TE» (как стороны квадрата). Но именно здесь отчётливо обнаруживается, что все эти определения идут по построению, и как бы «обратным ходом», то есть построение, очевидно, производилось именно так, чтобы можно было получить эти определения. В следующем краевом процессе применяется приём среднего пропорционального. Аристарх вводит новые чертёжные элементы и вводит их именно затем, чтобы создать непрерывную цепь взаимоотношений в чертежах. Все изложение материала в тексте исходит из уже готовых, построенных фигур, находящихся в определённых отношениях друг к другу, именно тех, которые нужны для решения задачи. Но само построение ведь тоже должно было осуществляться в соответствии с какими-то определёнными факторами, с помощью Вместе с тем именно в этом кусочке процесса мысли особенно отчётливо выступает связь «чертежных движений» и формальных соотношений, фиксирующих их результаты, и даже более того — известная зависимость первых от вторых. Одна из основных задач, очевидно, заключается в том, чтобы проанализировать эту зависимость. В четвёртом процессе («Но отношение отрезков GE и EH больше отношения дуг и значит…») мы совершенно ясно видим, что достаточно получить определённые соотношения в чертежах («отрезки — дуги»), чтобы можно было записать соотношение во второй плоскости. Но откуда и как получается эта система чертежей? Пятый переход вообще не фиксируется словесно: одна линия представляется как сумма своих частей. Шестой случай («Но в треугольнике ETF линия TG биссектриса угла ETF, поэтому TF:TE = FG:GE. Но квадрат, построенный на диагонали TF, вдвое более квадрата, построенного на TE или ET») требует специального и подробного анализа, который мы здесь не будем проводить; нам достаточно убедиться, что и здесь в основании лежат определённые соотношения чертёжных элементов, которые должны были быть заданы раньше построением. Но это совершенно очевидно, так как сложная система квадратов не возникает сама собой, а должна быть выбрана и построена. Итак, все процессы мышления, выделенные нами первоначально в краевые линии, оказываются неорганизованными, беспредметными и совершенно мистическими, если мы рассматриваем их изолированно, обособленно от общего контекста процесса мысли и от исходной задачи. Верхняя, формальная линия соотношений сама по себе не даёт связей; эти связи могут быть только в чертежном движении, а точнее — в процессе построения соответствующей системы чертежей. Но ведь нас интересует выделение целостных единиц в процессах мышления, которые затем можно будет употреблять в качестве эталонов разложения, и выявление законов построения сложных процессов мысли. Значит, мы можем и должны сделать вывод, что краевые процессы не могут быть такими единицами, а сам принцип анализа, приводящий к ним, ложен. Но даже если мы примем идею изображения рассматриваемого процесса мысли как цельного, единонаправленного движения, то и тогда перед нами во всей остроте будет стоять вопрос: а каково внутреннее строение этого процесса, какова последовательность движений и на какие единицы — линейные или структурные и многомерные — нужно раскладывать этот процесс? И, в частности, одним из основных вопросов будет тот, который мы уже наметили выше, рассматривая один из краевых процессов: в какой мере движение в чертежах, и именно построение, определяется характером словесно-алгебраических соотношений, которые нужно получить для решения задачи? Откуда идёт собственно мыслительное движение — от чертежа к знанию или от необходимости получить определённое знание (в данном случае — цепь формальных соотношений) к чертежу? Можно предположить, что задача ставится так: установить непрерывный ряд формальных соотношений. Средство её решения — создание «чертежной» системы, в которой существовали бы такие отношения и связи между чертёжными элементами, которые дают основание для искомой цепи словесно-алгебраических (или словесно-арифметических) соотношений. Движение мысли идёт от задачи к средству и затем — от одних элементов средства к другим. Но, во-первых, собственно у Аристарха, Можно, Чтобы понять, как этот способ решения превратился в более формальный и одновременно более компактный, свернутый, наш современный способ, нужно провести специальное генетическое исследование. Но уже то, что мы сейчас знаем, подтверждает основную для нас сейчас мысль, что у Аристарха движение шло, хотя и с учётом верхней плоскости и фиксируемых там результатов, но скорее в нижней плоскости самих чертежей, и именно там должны были фиксироваться в Во-вторых, этот вывод подтверждается тем, что ведь сама цепь формальных отношений, её состав, определяется возможностями чертёжного построения. Её элементы не заданы изначала как условие, они не определены однозначно, их подбор — лишь следствие того или иного движения в чертежах и будет таким на всех этапах развития мышления. Эти два соображения приводят нас к выводу, что процесс решения рассматриваемой задачи ни в коем случае нельзя представлять как изолированные (или относительно изолированные) движения в одной из плоскостей. Они не являются также и двумя параллельными, совершающимися относительно независимо и лишь соответствующими друг другу движениями. Вернее всего, что это — единое движение, которое в равной мере определяется как своей задачей — перевести отношение одних величин в отношение других или, позднее, установить непрерывный ряд соотношений, так и возможностями движения в чертежах. Это единое движение содержит, К примеру, после того, как на основе определённого движения в чертежах, найдено промежуточное соотношение, мы вновь возвращаемся к чертежам и ищем среди их элементов такое отношение, которое могло бы дать соотношение, связывающее данное отношение с новым в промежуточном соотношении. Таким образом поиск и движение в чертежах определяется задачей, которая фактически существует как задача получения определённого знания или определённого выражения. Таким образом, определённая характеристика продукта из верхней плоскости определяет характер познавательного движения в нижней плоскости, то есть в плоскости объектов. Собственно это обстоятельство и обнаруживает прежде всего, что мы имеем дело с единым целостным движением, а не с двумя просто тесно связанными между собой. Но чтобы проанализировать этот единый процесс, мы должны начать с анализа построений, то есть движений в собственно объектах, определяя попутно, чем обусловливается каждый шаг в них. Мы должны построить весь этот процесс мышления «снизу», исходя сначала из действий с первыми, начальными объектами, затем учитывая первые их заместители и действия с ними, ещё после — вторые заместители и так далее. Но это, в свою очередь, упирается в решение вопросов, которые были поставлены в конце предшествующего параграфа: каковы познавательные действия с объектами разных слоёв и в каких условиях при решении задач происходит переход от одного слоя заместителей к другому? Обсуждение этих вопросов — а систематически оно может быть проведено лишь в контексте восходящего исследования — должно стать темой ближайшей работы. |
|||||||||||
Примечания: |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||
Оглавление |
|||||||||||
|
|||||||||||