Карл Поппер:
Предположения и опровержения. Рост научного знания.
Часть I. Предположения.
Глава 2. Природа философских проблем и их корни в науке

Часть I

После некоторых колебаний я решил в качестве исходного пункта избрать современное состояние английской философии. Задача учёного или философа, как мне представляется, заключается скорее в том, чтобы решать научные или философские проблемы, нежели говорить о том, что он сам или другие философы сделали или могли бы сделать. Любая, даже неудачная, попытка решить научную или философскую проблему, если это честная и искренняя попытка, кажется мне более важной, чем обсуждение таких вопросов, как «Что такое наука?» или «Что такое философия?» И даже если последний вопрос мы сформулируем несколько лучшим образом: «Каков характер философских проблем?», я не стал бы особенно беспокоиться по поводу его решения, ибо чувствую, что он имеет слишком небольшое значение даже по сравнению со столь мелкой проблемой философии, как вопрос о том, всегда ли обсуждение или критика должны опираться на такие «допущения» или «предположения», которые сами остаются вне критики. ¹

Утверждая, что вопрос «Каков характер философских проблем?» является улучшенной формулировкой вопроса «Что такое философия?», я хочу указать на одну из причин тщетности современных споров относительно природы философии: наивную веру в то, что существует такая сущность, как «философия» или, может быть, «философская деятельность», и что она обладает определёнными чертами, сущностью или «природой». Вера в то, что существует такая вещь, как физика, биология или археология, и что эти «исследования» или «дисциплины» отличаются предметами исследования, представляется мне отголоском той эпохи, когда верили в то, что теория начинает с определения своего предмета ².

Однако я считаю, что предмет или разновидности вещей не создают основы для различения дисциплин. Дисциплины отличаются друг от друга отчасти в силу исторических причин и административных соображений (организация обучения и распределение финансирования), а отчасти потому, что теории, которые мы строим для решения наших проблем, имеют тенденцию ³ вырастать в специальные системы.

Однако все эти классификации и дистинкции сравнительно несущественны и поверхностны. Мы исследуем не предметы, а проблемы. Проблемы же способны пересекать границы любых дисциплин и их предметов.

Сколь бы очевидным ни казался этот факт некоторым людям, он настолько важен для нашего анализа, что заслуживает хотя бы иллюстрации посредством примера. Едва ли стоит напоминать о том, что проблемы геологии — скажем, оценка шансов обнаружить залежи нефти или урана в том или ином районе — решаются с помощью теорий и технических средств, обычно относимых к математике, физике и химии. Менее очевидно, однако, то обстоятельство, что даже более «базисные» науки, такие, скажем, как атомная физика, могут использовать геологические исследования, теории и технику геологии для решения проблем самых абстрактных и фундаментальных теорий, например, проблемы проверки предсказаний об относительной стабильности или нестабильности атомов с чётными или нечётными квантовыми числами.

Я вполне готов согласиться с тем, что многие проблемы, даже когда их решение опирается на далеко расходящиеся дисциплины, «принадлежат» в некотором смысле к одной и той же традиционной дисциплине. Две упомянутые выше проблемы очевидно «принадлежат» геологии и физике. Это обусловлено тем, что каждая из них была поставлена в ходе развития определённой дисциплины. Проблема возникает при обсуждении определённой теории или при её эмпирической проверке, а теории в отличие от предмета изучения способны образовать конкретную науку (которую можно истолковать как более или менее неопределённый набор теорий, способный изменяться и расти). Однако это не затрагивает моего утверждения о том, что разделение на дисциплины сравнительно несущественно и что мы изучаем не дисциплины, а проблемы.

Однако существуют ли философские проблемы?

Современная английская философия, воспринявшая, как мне представляется, учение покойного профессора Витгенштейна, считает, что таковых проблем не существует; что все подлинные проблемы являются научными; что так называемые проблемы философии являются псевдопроблемами; что мнимые утверждения или теории философии являются псевдоутверждениями и псевдотеориями; что их нельзя считать даже ложными (если бы они были ложными, то их отрицания следовало бы признать истинными утверждениями и теориями), ибо это просто бессмысленные наборы слов ⁴, имеющие не большее значение, чем лепет младенца, который ещё не научился правильно говорить ⁵.

Вследствие этого философия не может содержать каких-либо теорий. Истинная природа философии, согласно Витгенштейну, выражается не в теориях, а в деятельности. Задача всякой подлинной философии заключается в том, чтобы разоблачать философские бессмыслицы и учить людей говорить осмысленно. Это учение ⁶ Витгенштейна я хочу принять в качестве своего отправного пункта. Я попытаюсь объяснить его (в разделе II); до некоторой степени защитить его и подвергнуть критике (в разделе III). Затем я проиллюстрирую всё это (в разделах IV–XI) на некоторых примерах из истории научных идей.

Но прежде чем перейти к осуществлению своего плана, я хочу ещё раз повторить своё утверждение о том, что философ должен философствовать, он должен пытаться решать философские проблемы, а не говорить о философии. Если бы учение Витгенштейна было истинно, то никто не смог бы философствовать. И если бы я придерживался его мнения, я бросил бы философию.

Однако так случилось, что меня не только глубоко волновали определённые философские проблемы (не важно, «правильно» ли называть их «философскими» проблемами), но и существовала некоторая надежда на то, что я смогу внести свой вклад — пусть небольшой и только за счёт тяжёлого труда — в их решение. Моё стремление говорить здесь о философии, а не философствовать, несколько оправдывается надеждой на то, что осуществление намеченной программы даст нам удобный случай немного и пофилософствовать.

Часть II

Вместе с возникновением гегельянства появился опасный разрыв между наукой и философией. Философов обвиняли (и справедливо, я думаю) в том, что они «философствуют, не зная фактов», а их философские системы характеризовали как «примитивные и глупые фантазии» ⁷. Хотя гегельянство пользовалось большим влиянием в Англии и на континенте, противодействие ему и насмешки над его претенциозностью никогда вполне не умирали. Его ниспровержение было осуществлено философом, который — подобно Лейбницу, Беркли и Канту до него — имел здравое представление о науке, в частности, о математике. Я имею в виду Бертрана Рассела.

Расселу также принадлежит классификация, тесно связанная с его знаменитой теорией типов и послужившая основой для истолкования философии Витгенштейном, — классификация (критикуемая ниже в гл. 14) языковых выражений на:

• (1) истинные высказывания;
• (2) ложные высказывания;
• (3) бессмысленные выражения, в число которых входят похожие на высказывания последовательности слов, так называемые «псевдопредложения».

Это различие Рассел использовал для решения проблемы открытых им логических парадоксов. Для его решения наиболее существенным было различие между (2) и (3). На своём обыденном языке мы могли бы сказать, что ложные высказывания типа «3 умножить на 4 равно 173» или «Все кошки являются коровами» бессмысленны. Однако Рассел называет «бессмысленными» такие выражения, как «3 умножить на 4 равняется корове» или «Все кошки равны 173», которые не следует считать ложными высказываниями. Их не следует считать ложными, ибо отрицание осмысленного ложного высказывания всегда будет истинным.

Однако отрицание псевдопредложения «Все кошки равны 173» — «Все кошки не равны 173» — является таким же псевдопредложением, как и первоначальное выражение. Отрицания псевдопредложений сами являются псевдопредложениями, в то время как отрицания подлинных предложений (не важно, истинных или ложных) являются также подлинными предложениями (соответственно, ложными или истинными).

Это разграничение позволило Расселу устранить парадоксы (которые, как он считал, были бессмысленными псевдопредложениями).

Витгенштейн пошёл дальше. Подозревая, что философы — в частности, гегельянцы — говорят что-то очень похожее на парадоксы логики, он воспользовался расселовским различением для того, чтобы объявить всякую философию полностью бессмысленной.

Следовательно, не может существовать подлинно философских проблем. Все так называемые философские проблемы можно разбить на четыре группы ⁸:

1. Те, которые являются чисто логическими или математическими, требуют логического или математического решения и, следовательно, не являются философскими.
2. Те, которые являются фактуальными, требуют решения от эмпирической науки и, следовательно, опять-таки не являются философскими.
3. Проблемы, представляющие собой комбинацию (1) и (2), тоже не являются философскими; наконец.
4. Бессмысленные псевдопроблемы, например, «Являются ли все кошки равными 173?», «Является ли Сократ тождественным?» или «Существует ли невидимый, невоспринимаемый и непознаваемый Сократ?».

Идея Витгенштейна уничтожить философию (и теологию) с помощью расселовской теории типов была остроумна и оригинальна (и даже более радикальна, чем позитивизм Конта, которому она близка) ⁹. Эта идея вдохновила влиятельную современную школу анализа языка — школу, представители которой восприняли убеждение Витгенштейна в том, что подлинно философских проблем не существует и что задача философа заключается в разоблачении и устранении языковых головоломок, порождённых традиционной философией.

Я же считаю, что философия интересует меня лишь постольку, поскольку я занят решением подлинно философских проблем. Я не понимаю, чем может привлечь философия, если в ней нет проблем. Конечно, мне известно, что многие люди высказывают бессмыслицу, и я вполне допускаю, что кто-то может заняться неприятным делом разоблачения бессмысленностей, особенно если они опасны. Однако мне представляется, что хотя иногда люди высказывают не очень осмысленные вещи и не очень хорошо соблюдают правила грамматики, их высказывания весьма интересны и поучительны, они более ценны, нежели многие вполне осмысленные речи. Я могу упомянуть дифференциальное и интегральное исчисление, которое в своих ранних формах было совершенно парадоксально и бессмысленно с точки зрения стандартов Витгенштейна (и других). Однако оно получило вполне разумное обоснование в результате столетних усилий великих математиков и даже в наши дни все ещё продолжаются поиски дальнейшего прояснения его оснований ¹⁰.

В этой связи мы могли бы вспомнить о контрасте между внешней абсолютной точностью математики и неопределённостью и неточностью философского языка — контрасте, который произвёл глубокое впечатление на первых последователей Витгенштейна. Однако если бы какой-нибудь Витгенштейн направил своё оружие против основоположников дифференциального исчисления и подавил бы их попытки как выражение бессмыслицы, чего не удалось сделать их современникам (например, Беркли, который по существу был прав), то он задушил бы одно из наиболее плодотворных и философски важных направлений в истории человеческой мысли.

Витгенштейн как-то написал: «О чём нельзя говорить, о том следует молчать». На это Эрвин Шрёдингер, если я не ошибаюсь, ответил: «Но только об этом и следует говорить» ^10а. История дифференциального исчисления и, возможно, собственной теории Шрёдингера ¹¹ подтверждают это.

Безусловно, все мы должны стремиться к тому, чтобы говорить настолько ясно, точно и просто, насколько можно. Тем не менее, как мне представляется, если взять работы классиков науки и математики или просто книги, заслуживающие прочтения, то с помощью умелого применения техники языкового анализа можно показать, что в них содержится немало бессмысленных псевдопредложений или того, что называют «тавтологиями».

Более того, я думаю, что даже первоначальное применение теории Рассела Витгенштейном основывалось на логической ошибке. С точки зрения современной логики, уже нельзя больше говорить о псевдопредложениях или типичных ошибках в обыденных, естественных языках (в отличие от формальных исчислений), если учитывать конвенциональные правила и обычаи грамматики. Можно было бы даже сказать, что позитивист, с воодушевлением неофита провозглашающий, что мы пользуемся бессмысленными словами или произносим бессмыслицу, сам не знает, о чём говорит, — он просто повторяет то, что услышал от других, которые также не знают. Правда, здесь возникают технические проблемы, на которых сейчас я не хочу останавливаться. (Они рассматриваются в гл. 11–14.)

Часть III

Я обещал сказать кое-что в защиту позиции Витгенштейна. Во-первых, я согласен с тем, что имеется немало философских сочинений (в частности, представителей гегелевской школы), которые действительно заслуживают критики за бессмысленное пустословие. Следует отметить, во-вторых, что по крайней мере на время такого рода сочинения были дискредитированы благодаря усилиям Витгенштейна и представителей языкового анализа (хотя наиболее плодотворным в этом отношении было влияние Рассела, который в своих произведениях показал, каким образом глубину содержания можно сочетать с изяществом и простотой стиля).

Однако я готов пойти дальше и в своей защите Витгенштейна склонен отстаивать два следующих тезиса.

Первый тезис заключается в том, что каждая философия и особенно каждая философская «школа» со временем вырождается таким образом, что её проблемы становятся почти неотличимы от псевдопроблем, а её язык становится похож на бессмысленную болтовню. Я попытаюсь показать, что это является результатом философского кровосмешения. В свою очередь, вырождение философских школ является следствием ошибочной веры в то, что можно философствовать, не обращаясь к проблемам, возникающим за пределами философии, — например, в математике, космологии, политике, религии или в общественной жизни. Иными словами, мой первый тезис гласит: подлинно философские проблемы всегда вырастают из проблем, возникающих вне философии, и они умирают, если эта связь прерывается. В своих усилиях решить философские проблемы философы разрабатывают что-то похожее на философский метод или специальную технику достижения успеха ¹².

Однако таких методов или технических средств не существует. В философии методы не важны, любой метод оправдан, если приводит к результату, заслуживающему рационального обсуждения. Важны не методы, а чуткость по отношению к проблемам и стремление к их решению или, как говорили греки, способность удивляться.

Существуют люди, испытывающие потребность решить некоторую проблему, люди, для которых проблема становится реальной — как некий беспорядок в их личной системе ¹³. Они способны внести вклад в её решение, даже если привязаны к конкретному методу или технике. Однако имеются и другие авторы, не испытывающие такой потребности, у которых нет серьёзной и привлекательной проблемы, но они тем не менее упражняются в использовании модных методов. Для них философия является применением (какой-то концепции или техники, если угодно), а не исследованием. Они завлекают философию в болото псевдопроблем и словесных ухищрений, либо выдавая псевдопроблемы за реальные проблемы (опасность, которую видел Витгенштейн), либо убеждая нас заняться бесконечным и бесплодным разоблачением того, что они верно или неверно считают псевдопроблемами или «головоломками» (в эту ловушку попал Витгенштейн).

Второй тезис состоит в том, что prima facie (Здесь и далее: первоначальный (лат). — Прим. ред.) метод обучения философии создаёт философию, отвечающую описанию Витгенштейна. Под «prima facie методом обучения философии», который может показаться единственным методом, я имею в виду такой способ действий, когда начинающего (который не знаком с историей математических, космологических и других идей науки и политики) заставляют читать работы великих философов, скажем, Платона и Аристотеля, Декарта и Лейбница, Локка, Беркли, Юма, Канта и Милля. Каков эффект такого чтения? Перед читателем открывается новый мир удивительно тонких и широких абстракций — абстракций чрезвычайно высокого и сложного уровня. Перед его сознанием предстают идеи и рассуждения, которые не только трудно понять, но которые кажутся читателю ненужными, ибо он не знает, для чего они могли бы пригодиться. Однако студент понимает, что это великие философы и они создавали философию. Поэтому он будет стремиться заставить себя мыслить так, как мыслили (по его мнению, которое, как мы увидим, ошибочно) эти философы. Он будет пытаться усвоить их странный язык, понять прихотливые изгибы их рассуждений и погрузиться в их странные проблемы.

Одни скользнут поверхностно по этим ходам мысли, другие увлекутся ими, как наркотиком. Тем не менее, мне кажется, нужно с уважением отнестись к человеку, затратившему много усилий для того, чтобы в конечном итоге прийти к выводу, сделанному Витгенштейном: «Я усвоил этот жаргон так же хорошо, как любой другой. Он прост и привлекателен. На самом же деле, это опасная привлекательность, ибо простая истина состоит в том, что здесь много шума из ничего, только бессмыслица».

Теперь этот вывод кажется мне совершенно ошибочным, хотя это почти неизбежный результат prima facie обучения философии. (Конечно, я не хочу спорить с тем, что отдельные одарённые студенты могут найти в работах великих философов гораздо больше, чем было указано, причём без самообмана.) Шансов обнаружить внефилософские проблемы (математические, научные, моральные и политические), вдохновлявшие великих философов, у студента очень мало. Эти проблемы, как правило, можно открыть только благодаря изучению истории, например, научных идей и, главным образом, проблемных ситуаций в математике и науке того или иного периода, а это, в свою очередь, предполагает основательное знакомство с математикой и наукой. Только в том случае, если студент понимает современную проблемную ситуацию в тех или иных науках, он может понять, что великие философы прошлого пытались решать настоятельные и конкретные проблемы — проблемы, от которых они не могли уйти. Лишь такое понимание способно дать студенту верное представление о великих философских системах и придать смысл кажущейся бессмыслице.

Свои тезисы я хочу обосновать с помощью примеров, однако прежде чем переходить к этим примерам, я хотел бы кратко выразить основную идею этих тезисов и определить своё отношение к Витгенштейну.

Два моих тезиса равнозначны утверждению о том, что поскольку философия глубоко укоренена в нефилософских проблемах, постольку негативная оценка Витгенштейном философских систем, оторвавшихся от своих внефилософских корней, в значительной мере справедлива. Об этих корнях легко забывают те философы, которые «изучают» философию вместо того, чтобы заниматься ей под давлением внефилософских проблем.

Моё отношение к учению Витгенштейна кратко можно выразить следующим образом. Возможно, в значительной мере верно, что «чисто» философских проблем не существует. Чем чище становится философская проблема, тем больше она теряет своё первоначальное значение и тем быстрее её обсуждение вырождается в пустую словесную эквилибристику. С другой стороны, существуют не только подлинно научные, но и подлинно философские проблемы. Даже если в этих проблемах обнаруживаются фактуальные компоненты, их нельзя считать проблемами науки. И даже если они решаются, скажем, чисто логическими средствами, их нельзя характеризовать как чисто логические или тавтологические.

Аналогичные ситуации возникают, например, в физике. Скажем, проблему объяснения серий спектральных линий (с помощью гипотезы относительно структуры атомов) можно решить чисто математическими вычислениями. Однако отсюда не следует, что данная проблема относится к математике, а не к физике. Мы вполне оправданно считаем проблему «физической», если она связана с проблемами и теориями, которые традиционно обсуждались физиками (например, проблема строения материи), даже когда средства её решения оказываются чисто математическими. Как мы видели, решение некоторых проблем может зависеть от многих наук. И точно так же некоторую проблему с полным правом можно называть «философской», даже если обнаруживается, что, хотя первоначально она возникла в связи, скажем, с атомной теорией, однако она более тесно связана с проблемами и теориями философии, чем с теми теориями, которыми сегодня занимаются физики. И опять-таки совершенно не важно, какого рода методы мы используем при решении таких проблем.

Космология, например, всегда будет вызывать большой интерес у философов, несмотря на то что некоторые её методы весьма близки тому, что лучше было бы назвать «физикой». Утверждать, что поскольку космология имеет дело с фактуальными вопросами, её следует относить к науке, а не к философии, было бы не только педантизмом, но, очевидно, эпистемологической, то есть философской, догмой. Аналогично, если некоторая проблема решается средствами логики, то нет никаких оснований отрицать её «философский» статус. Она может быть как философской, так физической или биологической. Логический анализ играл важную роль в специальной теории относительности Эйнштейна, и отчасти именно это сделало данную теорию интересной с философской точки зрения и породило широкий спектр философских проблем, связанных с ней.

Учение Витгенштейна оказывается следствием тезиса, утверждающего, что все подлинные предложения (следовательно, все подлинные проблемы) можно разбить на два взаимоисключающих класса: фактуальные предложения (synthetic a posteriori), относящиеся к эмпирическим наукам, и логические предложения (analytic a priori), принадлежащие к чистой логике и математике. Эта простая дихотомия, весьма ценная для первичного исследования, для многих целей оказывается слишком простой ¹⁴. Несмотря на то что она специально была предназначена для того, чтобы исключить существование философских проблем, она оказалась совершенно недостаточной для достижения этой цели. Даже если принять эту дихотомию, мы все ещё можем считать, что фактуальные, логические или смешанные проблемы при некоторых обстоятельствах могут оказаться философскими.

Часть IV

Теперь я обращаюсь к своему первому примеру: Платон и кризис раннего греческого атомизма.

Я утверждаю, что центральное философское учение Платона, его так называемую теорию форм или идей, нельзя правильно понять без обращения к внефилософскому контексту ¹⁵, точнее говоря, вне контекста критической проблемной ситуации, возникшей в греческой науке ¹⁶ (главным образом, в теории материи) в результате открытия иррациональности квадратного корня из двух. Если моё утверждение верно, то теория Платона до сих пор не была полностью понята. (Конечно, вопрос о том, можно ли вообще когда-нибудь получить «полное» понимание, является в высшей степени спорным.) Однако более важное следствие состоит в том, что она никогда не может быть понята философами, получившими своё образование посредством prima facie метода, описанного в предшествующем разделе, если, конечно, они специально и ad hoc не познакомились с соответствующими фактами. (Но в таком случае это означает отказ от prima facie метода изучения философии.)

Представляется весьма правдоподобным ¹⁷, что и в своём происхождении, и в своём содержании теория форм Платона была тесно связана с учением пифагорейцев о том, что сущностью всех вещей являются числа.

Однако детали этой связи и взаимоотношения между атомизмом и пифагорейством известны не очень хорошо. Поэтому я кратко остановлюсь здесь на этой истории и изложу её так, как она мне представляется сегодня.

По-видимому, основатель пифагорейской школы испытал глубокое воздействие двух открытий. Первое заключалось в том, что такое prima facie совершенно качественное явление, как музыкальная гармония, опиралось, по сути дела, на чисто числовые соотношения 1:2; 2:3; 3:4. Второе открытие состояло в том, что «прямой» угол (получаемый, например, посредством сгибания листа так, чтобы складки образовали крест) был связан с чисто числовыми отношениями 3:4:5 или 5:12:13 (стороны прямоугольных треугольников). Вот эти два открытия привели пифагорейцев к несколько фантастическому обобщению, гласящему, что вещи по сути своей являются числами или числовыми соотношениями, что числа являются ratio (logos = reason), рациональной сущностью вещей или их подлинной природой.

Сколь бы фантастичной ни была эта идея, во многих отношениях она доказала свою плодотворность. Одним из наиболее успешных было её применение к простым геометрическим фигурам — квадратам, прямоугольникам, равнобедренным треугольникам, а также к некоторым простым телам, например, пирамидам.

Анализ некоторых из этих геометрических проблем опирался на так называемый гномон.

Суть дела можно пояснить следующим образом. Если указать квадрат посредством четырёх точек:

То его можно интерпретировать как результат добавления трёх точек к одной, находящейся в левом верхнем углу. Эти три точки образуют гномон, который можно указать так: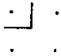

Добавляя сюда второй гномон, состоящий из пяти точек, мы получаем: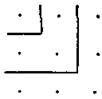

Легко заметить, что множества добавляемых точек 1, 3, 5, 7… образуют гномон квадрата, что суммы 1,1 + 3,1 + 3 + 5,1 + 3 + 5 + 7… являются квадратами чисел и что если n (число точек) есть сторона квадрата, его площадь (общее число точек = n²) будет равна сумме первых добавленных чисел.

Точно так же можно истолковать равнобедренный треугольник. Следующая фигура представляет растущий треугольник — растущий благодаря добавлению новых горизонтальных наборов точек:

Здесь каждый гномон представляет собой горизонтальную линию точек и каждый элемент последовательности 1, 2, 3, 4… является гномоном.

«Треугольные числа» являются суммами 1 + 2; 1 + 2 + 3; 1 + 2 + 3 + 4 и так далее, то есть суммами первых n натуральных чисел. Расположив два таких треугольника друг против друга: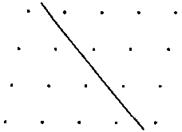

Мы получим параллелограмм с горизонтальной стороной n + 1, другой стороной n и содержащей n (n + I) точек. Поскольку он состоит из двух равнобедренных треугольников, его числом будет 2 (1 + 2 + … + n), поэтому мы получаем равенство:

(1) 1 + 2 + … + n = 7₂ n (n + 1); следовательно:

(2) d (l + 2 + … + 2) = % n (2 + 1).

Отсюда легко получается общая формула для суммы арифметических серий.

Точно так же мы получаем «прямоугольные» числа, то есть числа неравнобедренных прямоугольников, простейшим из которых будет следующий: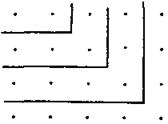

С прямоугольными числами 2 + 4 + 6… Гномоном прямоугольного числа является четное число и прямоугольные числа являются суммами чётных чисел.

Эта трактовка может быть распространена и на геометрические тела, например, суммируя первые треугольные числа, мы получаем пирамидальные числа. Однако главной областью её применения были плоские фигуры, образы или «формы». Считалось, что формы могут быть охарактеризованы подходящими последовательностями чисел и числовыми соотношениями. Иными словами, «формы» являются числами или соотношениями чисел. С другой стороны, не только формы вещей, но и такие абстрактные свойства, как гармония или «прямизна», также являются числами. Вот так приходят к общей теории, гласящей, что числа являются умопостигаемой сущностью всех вещей.

Вероятно, на разработку этой точки зрения оказало влияние сходство диаграмм точек со схемами созвездий — Льва, Скорпиона, Девы.

Если Лев есть упорядоченная совокупность точек, то он должен обладать числом.

Здесь можно заметить связь пифагорейства с верой в то, что числа, или «формы», являются небесными образами вещей.

Одной из главных составных частей этой ранней теории была так называемая «таблица оппозиций», опиравшаяся на фундаментальное различие между нечётными и чётными числами. В неё входили такие элементы:

Просматривая эту странную таблицу, получаешь некоторое представление о мышлении пифагорейцев и начинаешь понимать, почему не только «формы» или образы геометрических фигур считались, по сути своей, числами, но также и абстрактные идеи, такие как Справедливость, Гармония и Здоровье, Красота и Знание. Эта таблица интересна ещё и потому, что с небольшими изменениями она была принята Платоном. Самый ранний вариант знаменитой теории «форм», или «идей», Платона приблизительно можно описать как учение о том, что сторона «Добра» в таблице оппозиций образует (невидимый) универсум — универсум высшей реальности, универсум неизменных и определённых «форм» всех вещей.

Истинное и определённое знание (episteme = scientia = science) может относиться только к этому неизменному и реальному универсуму, в то время как видимый, изменчивый и текучий мир, в котором мы живём и умираем, мир рождения и разрушения, мир опыта представляет собой лишь отражение или копию этого реального мира. Это лишь мир явлений, относительно которого нельзя получить истинного и определённого знания. Место знания (episteme) здесь занимают неопределённые и неполноценные мнения (doxa) подверженных ошибкам смертных ¹⁸. В своей интерпретации таблицы оппозиций Платон испытал влияние Парменида — человека, смелый вызов которого привёл к разработке атомистической теории Демокритом.

Часть VI

Теория пифагорейцев с её диаграммами точек, несомненно, намекала на очень примитивный атомизм. Трудно сказать, в какой мере атомистическая теория Демокрита испытала влияние пифагорейцев. Гораздо более несомненным представляется влияние элеатов — Парменида и Зенона. Наиболее важной проблемой для школы элеатов и Демокрита была проблема рационального истолкования изменения. (Я отхожу здесь от интерпретации Корнфорда и других авторов.) Я считаю, что эта проблема восходит к Гераклиту и идеям ионийских философов, а не к пифагорейцам ¹⁹, и она всё ещё остаётся фундаментальной проблемой натуральной философии.

Хотя Парменид, по-видимому, не был физиком (в отличие от своих великих ионийских предшественников), его можно, как мне кажется, считать основоположником теоретической физики. Он создал антифизическую ²⁰ (а не не-физическую, как считал Аристотель) теорию, которая тем не менее была первой гипотетико-дедуктивной системой. Она положила начало длинной последовательности таких систем физических теорий, каждая из которых была улучшением своих предшественниц.

Как правило, улучшения признавались необходимыми в результате осознания того, что прежняя система была фальсифицирована определёнными опытными фактами. Такое эмпирическое опровержение следствий дедуктивной системы вело к её реконструкции и, таким образом, к созданию новой улучшенной теории, которая обычно сохраняла следы своего происхождения — предшествующей теории и опровергающего опыта.

Этот опыт или наблюдения вначале, как мы увидим, были очень грубыми, однако они становились всё более тонкими по мере того, как возрастала способность теорий к ассимиляции грубых наблюдений. В случае с теорией Парменида её столкновение с наблюдением было столь очевидным, что, может быть, не стоит считать её первой гипотетико-дедуктивной системой физики. Лучше назвать её последней до-физической дедуктивной системой, опровержение или фальсификация которой дала начало первой физической теории материи — атомистической теории Демокрита.

Теория Парменида проста. Он находит, что рациональное понимание изменения или движения невозможно, и делает вывод о том, что изменение не является реальным или является лишь видимостью. Не будем с пренебрежением отворачиваться от этой очевидно нереалистической теории, попробуем сначала понять, что здесь имеется серьёзная проблема. Если вещь X изменилась, то ясно, что это уже не та же самая вещь X. С другой стороны, мы не можем сказать, что X изменилась, не подразумевая при этом, что X как-то сохраняется в процессе изменения, что и в начале, и в конце изменения это всё та же вещь X. Таким образом, кажется, что мы приходим к противоречию и что мысль о вещи, которая изменяется, следовательно, идея изменения невозможны.

Все это звучит весьма абстрактно и философично, и так оно и есть. Однако фактом является то, что указанная здесь трудность постоянно ощущалась в развитии физики ²¹. Атакую детерминистскую систему, как теория поля Эйнштейна, можно даже истолковать как четырёхмерный вариант парменидовского неизменного трёхмерного универсума. В четырёхмерном универсуме Эйнштейна также, в некотором смысле, не происходит никаких изменений. Все вещи остаются на своих четырёхмерных траекториях, а изменения становятся лишь «кажущимися».

«Только лишь» наблюдатель, движущийся вдоль своей мировой линии, замечает последовательную смену разных мест на этой мировой линии, то есть в своём пространственно-временном окружении… Вернувшись вновь к Пармениду, отцу теоретической физики, мы можем сформулировать его дедуктивную теорию приблизительно в следующем виде:

(1) Есть только то, что есть.

(2) Чего нет, того не существует.

(3) Небытие, то есть пустота, не существует.

(4) Мир полон.

(5) Мир не имеет частей; это одна громадная глыба (поскольку он полон).

(6) Движение невозможно (ибо не существует пустого пространства, в котором что-то могло бы двигаться).

Заключения (5) и (6) очевидно противоречат фактам.

Поэтому из ложности этих заключений Демокрит выводит ложность посылок:

(6’) Движение существует (поэтому оно возможно).

(5’) Мир имеет части; это не единое, а многое.

(4’) Поэтому мир не может быть полон ²².

(3’) Пустота (или небытие) существует.

Так была изменена теория. В отношении бытия, или множества существующих вещей (противопоставляемых пустоте) Демокрит принимает теорию Парменида, утверждая, что они не имеют частей. Они неразделимы (атомы), ибо они заполнены и не содержат в себе пустоты.

Основное достижение этой теории состоит в том, что она даёт рациональное истолкование движения. Мир состоит из пустого пространства (пустоты) и атомов в нём. Атомы не изменяются; они представляют собой неделимый универсум Парменида в миниатюре ²³. Все изменения обусловлены перераспределением атомов в пространстве. Поэтому всякое изменение есть движение. С этой точки зрения, может возникать лишь одно новое — новое расположение атомов ²⁴, поэтому, в принципе, возможно предсказать все будущие изменения в мире, если мы способны предсказать движение всех атомов (или на современном языке: всех материальных точек).

Теория изменения Демокрита имела громадное значение для развития физической науки. Частично она была принята Платоном, который в значительной мере сохранил атомизм, хотя и объяснял движение не только с помощью неизменных движущихся атомов, но и с помощью других «форм», которые сами не испытывали ни изменения, ни движения. Однако Аристотель её осуждал, полагая ²⁵, что всякое изменение является развёртыванием внутренних потенций существенно неизменных субстанций. Аристотелевская теория субстанций как объектов изменения стала доминирующей. Однако она оказалась бесплодной ²⁶, и метафизическая теория Демокрита, утверждающая, что все изменения следует объяснять движением, превратилась в неявно принимаемую программу действий физиков вплоть до настоящего времени. Она все ещё является частью философии физики, хотя сами физики уже переросли её (чего нельзя сказать о биологических и социальных науках). В дополнение к движущимся материальным точкам на сцену со времён Ньютона выступили силы изменения, напряжения (и направления).

Верно, конечно, что изменения ньютоновских сил можно объяснить как обусловленные движением, то есть изменением положений частиц. Тем не менее они не тождественны изменениям положений частиц, а квадратичный закон даже не является линейным.

После работ Фарадея и Максвелла изменения силовых полей становятся столь же важными, как и изменения материальных атомных частиц. То обстоятельство, что наши современные атомы оказываются сложными, не имеет большого значения. С точки зрения Демокрита, атомами должны быть не наши нынешние атомы, а скорее наши элементарные частицы, если не обращать внимания на тот факт, что они тоже подвержены изменениям. Таким образом, возникает чрезвычайно интересная ситуация. Философия изменения, предназначенная для преодоления трудностей рационального понимания изменения, на протяжении тысячелетий служила науке и в конечном счёте была превзойдена развитием самой науки. К сожалению, этот факт практически не был замечен теми философами, которые настойчиво отрицают существование философских проблем.

Теория Демокрита была громадным достижением. Она предложила теоретическую структуру для объяснения большей части эмпирически обнаруженных свойств материи (рассматривавшихся уже ионийцами) — сжимаемость, степени твёрдости и упругости, разрежение и сгущение, связность, разрушение, горение и многие другие. Однако значение этой теории не исчерпывалось только тем, что она объясняла явления опыта. Во-первых, она дала обоснование тому методологическому принципу, что дедуктивная теория и объяснение должны «спасать феномены» ²⁷, то есть должны согласоваться с опытом. Во-вторых, она показала, что теория может носить спекулятивный характер и опираться на фундаментальный принцип (Парменида), говорящий о том, что мир в понимании его мыслью отличается от мира prima facie опыта — мира зрения, слуха, обоняния, вкуса, осязания ²⁸.

Тем не менее такая спекулятивная теория может принять эмпирический «критерий», согласно которому видимое играет решающую роль в признании или отвержении теории невидимого ²⁹ (скажем, атомов). Эта философия оставалась фундаментом всего развития физики и вступала в конфликт со всеми «релятивистскими» и «позитивистскими» ³⁰ философскими тенденциями.

Кроме того, теория Демокрита привела к первым успехам метода исчерпывания (предвосхитившего интегральное исчисление), ибо сам Архимед признал, что Демокрит первым сформулировал теорию объёмов конусов и пирамид ³¹.

Однако наиболее удивительной, быть может, частью теории Демокрита является его учение о квантованности пространства и времени. Я имею в виду ныне широко обсуждаемую ³² мысль о том, что существуют минимальные расстояния и минимальные временные интервалы, то есть что в пространстве и времени существуют такие величины (элементы длины и времени, ameres ³³Демокрита, отличные от его атомов), которые являются предельно малыми.

Часть VII

Атомизм Демокрита был разработан в качестве основы для ответа ³⁴ на аргументы его предшественников-элеатов — Парменида и его ученика Зенона. В частности, его теория атомарных расстояний и временных интервалов была непосредственным результатом аргументов Зенона или, точнее, отрицания выводов Зенона. Однако теперь из того, что нам известно о Зеноне, мы можем усмотреть намёк на открытие иррациональных величин — открытие, имевшее решающее значение для нашей истории.

Мы не знаем даты доказательства иррациональности квадратного корня из двух или даты, когда это открытие получило известность.

Хотя и существует традиция приписывать его Пифагору (VI век до Новой эры) и некоторые авторы ³⁵ называют его «теоремой Пифагора», трудно сомневаться в том, что это открытие не было сделано и, во всяком случае, не было известно до 450 года до Новой эры, скорее даже до 420 года. Неясно, было ли оно известно Демокриту. Теперь я склонен считать, что он не знал об этом открытии и что названия двух последних книг Демокрита «Peri alagцn grammцn kai naston» следует переводить как «О нелогичных отрезках и полных телах (атомах)» ³⁶ и что эти две книги не содержали каких-либо ссылок на открытие иррациональности ³⁷.

Моё убеждение в том, что Демокрит не осознавал проблемы иррациональности, опирается на тот факт, что нет никаких следов, указывающих на то, что он хотел защитить свою теорию от удара, который наносило ей это открытие. Однако этот удар оказался фатальным как для атомизма, так и для пифагорейства. Обе теории исходили из учения о том, что всякое измерение в конечном счёте сводится к подсчёту естественных единиц, так что каждое измерение должно выражаться числом. Следовательно, расстояние между любыми атомными точками должно состоять из определённого числа атомных расстояний; таким образом, все отрезки должны быть соизмеримы. Однако это оказывается невозможным даже для простого случая расстояний между углами квадрата вследствие несоизмеримости его диагонали d со стороной a.

Английский термин «несоизмеримый» несколько неудачен.

В нём подразумевается несуществование соотношения натуральных чисел, например, можно доказать для квадрата со стороной, равной единице, что не существует таких двух натуральных чисел n и t, отношение которых n/t равно диагонали этого квадрата. Таким образом, «несоизмеримость» не означает несравнимости с помощью геометрических методов или измерений, а только несравнимость на основе арифметических методов счета или на основании натуральных чисел, включая пифагорейский метод сравнения отношений натуральных чисел и, конечно, подсчёт единиц длины (или «меры»).

Возвратимся ненадолго к характеристике этого метода натуральных чисел и их соотношений. Превознесение Числа Пифагором оказало плодотворное влияние на развитие научных идей. Это часто, хотя и несколько неопределённо, выражают утверждением о том, что пифагорейцы стимулировали развитие количественного научного измерения. Я же настаиваю на том, что для пифагорейцев всё это было скорее счетом, чем измерением. Это был счёт чисел, невидимых сущностей, или «природ», которые были числами мельчайших точек. Они знали, что эти мельчайшие точки нельзя сосчитать непосредственно, ибо они невидимы, и что реально мы не считаем Числа или Естественные единицы, а измеряем, то есть считаем произвольные видимые единицы. Однако измерения они интерпретировали как косвенное раскрытие истинных соотношений Естественных единиц или натуральных чисел.

Метод доказательства Евклидом так называемой «теоремы Пифагора» (Евклид, 1, 47), согласно которому если а есть сторона прямоугольного треугольника, лежащая против прямого угла, образованного сторонами b и c, то (1) a² = b² + c² был чужд духу пифагорейской математики. Ныне считается, что эта теорема была известна уже вавилонянам и доказывалась ими геометрически. Однако ни Пифагор, ни Платон не могли знать геометрического доказательства Евклида (который использовал разные треугольники с общим основанием и высотой). Проблема, которую они решали, была арифметической задачей нахождения общего решения для сторон прямоугольных треугольников. Если равенство (1) известно, то эта задача может быть легко решена посредством следующей формулы (тип — натуральные числа и t > n) \ (2) a — t² + n²; b = 2 tn; с = t² — n². Однако формула (2) была, по-видимому, неизвестна как Пифагору, так и Платону. Согласно традиции ³⁸, Пифагор предложил следующую формулу (полученную из (2) посредством подстановки: t = n + (1) : (3) а = 2n (n + 1); b = 2(n + 1); c = 2n + 1.

Её можно истолковать как гномон квадратных чисел, хотя эта формула является менее общей, нежели формула (2), ибо она не будет верной, например, для 17 : 8 : 15. Платону, который улучшил ³⁹формулу Пифагора (3), приписывают другую формулу, которая всё-таки ещё не равнозначна общему решению (2).

Для иллюстрации разницы между пифагорейским, или арифметическим, методом и геометрическим методом следует упомянуть доказательство Платоном того факта, что квадрат диагонали единичного квадрата (то есть квадрата со стороной, равной 1) равен удвоенной единице в квадрате.

Доказательство заключается в изображении квадрата с диагональю: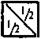

А затем в расширении этого изображения следующим образом: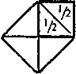

Отсюда искомый результат получается посредством счёта.

Однако переход от первого рисунка ко второму нельзя обосновать посредством арифметического подсчёта точек и даже посредством рациональных дробей.

Невозможность этого устанавливается знаменитым доказательством иррациональности диагонали, то есть квадратного корня из 2, — доказательством, хорошо известным Платону и Аристотелю. Это доказательство заключается в демонстрации того, что предположение:

(1) V 2 = n/t, гласящее, что V 2 равен рациональной дроби двух натуральных чисел n и t, приводит к противоречию. Сначала мы можем предположить, что:

(2) только одно из двух чисел n и t является чётным. Если бы оба числа были чётными, то мы всегда могли бы сократить их на 2 и получить два других числа n’ и t’, таких что  ⁿ/t = ⁿ’/t и> из которых лишь одно могло быть чётным. Возведя в квадрат обе части равенства (1), мы получаем:

(3) 2 = n²/t² а из этого получаем:

(4) 2t: ² = n² Таким образом, (5) n является чётным.

Это означает, что должно существовать такое натуральное число а, что:

(6) n = 2a. Теперь из (3) и (6) мы получаем:

(7) 2t² = n ² = a² из чего следует, что:

(8) t ² = 2а² Но это означает, что (9) t является чётным.

Ясно, что (5) и (9) противоречат допущению (2). Таким образом, предположение о том, что существуют два натуральных числа n и t, рациональная дробь которых равна V 2, приводит к абсурдному выводу. Следовательно, V 2 не является рациональной дробью, он «иррационален».

В этом доказательстве используется только арифметика натуральных чисел. Следовательно, здесь мы имеем дело с чисто пифагорейскими методами, поэтому не стоит спорить с традицией, приписывающей открытие этого доказательства пифагорейской школе. Однако невероятно, чтобы оно было сделано Пифагором или очень рано, ибо о нём не знал ни Зенон, ни Демокрит. Более того, поскольку оно подрывало основы пифагорейского учения, постольку можно предполагать, что это открытие не было сделано до того, как это учение достигло пика своего влияния, ибо оно должно было содействовать упадку этого учения.

Мысль о том, что оно было открыто в пифагорейской школе, но держалось в секрете, представляется мне вполне допустимой. В её пользу свидетельствует то обстоятельство, что старый термин для слова «иррациональный» — «arrhetos», «непроизносимый» или «не-упоминаемый» — вполне может указывать на скрываемый секрет. Традиция говорит о том, что члены школы, пытавшиеся раскрыть этот секрет, были убиты за предательство ⁴⁰. Так или иначе, но трудно сомневаться в том, что осознание существования иррациональных величин (которые, конечно, не считались числами) и возможности доказательства их существования подрывало веру в пифагорейское учение и надежду на то, что из арифметики натуральных чисел можно вывести космологию или хотя бы геометрию.

Часть VIII

Именно Платон осознал этот факт и выразительно подчеркнул его значение в «Законах», обвинив своих современников в неспособности оценить его следствия. Как мне представляется, влияние этого факта испытала на себе вся его философия и, в частности, его теория «форм» или «идей».

Платон был очень близок к пифагорейцам и к школе эле-атов, и хотя он, по-видимому, недолюбливал Демокрита, сам он был в некотором роде атомистом. (Атомистическое учение сохранялось в качестве одной из традиций Академии ⁴¹.) Это неудивительно, если принять во внимание тесную связь пифагорейства с идеями атомизма. Однако всё это оказалось под угрозой благодаря открытию иррациональности. Я полагаю, что главный вклад Платона в науку обусловлен его осознанием проблемы иррациональности и той модификацией пифагорейства и атомизма, которую он предпринял для спасения науки от катастрофы.

Он понял, что чисто арифметическая теория природы рухнула и нужен новый математический метод описания и объяснения мира. Поэтому он приступил к разработке самостоятельного геометрического метода. Своё наиболее полное воплощение этот метод нашёл в «Элементах» платоника Евклида.

Каковы факты? Я попытаюсь кратко суммировать их.

1. Учение пифагорейцев и атомизм Демокрита существенно опирались на арифметику, то есть на счёт.
2. Платон подчеркнул катастрофические последствия открытия иррациональности.
3. Над входом в Академию он написал: «Да не войдёт сюда никто, не знающий геометрии». Но геометрия, согласно прямому ученику Платона Аристотелю ⁴² и Евклиду, часто говорит о несоизмеримостях и иррациональности в отличие от арифметики, рассматривающей «четное и нечётное» (то есть целые числа и их отношения).
4. Вскоре после смерти Платона его школа в «Элементах» Евклида создала произведение, освободившее математику от «арифметического» предположения о соизмеримости и рациональности.
5. Платон и сам внёс вклад в это развитие, в частности, в разработку геометрии твёрдых тел.
6. Говоря точнее, в «Тимее» он предложил геометрический вариант ранее чисто арифметической атомной теории — вариант, в котором элементарные частицы (знаменитые платоновские Тела) строились из треугольников, включавших в себя иррациональные квадратные корни из двух и трех. (См. ниже.) Во всех других отношениях он сохраняет идеи пифагорейцев и наиболее важные идеи Демокрита ⁴³. В то же время он 147 устраняет пустоту Демокрита, ибо понимает ⁴⁴, что движение возможно даже в «заполненном» мире, если его истолковывать наподобие вихрей в жидкости. Таким образом, он сохраняет и некоторые из наиболее важных идей Парменида ⁴⁵.
7. Платон стимулировал создание геометрических моделей мира, в частности, моделей, объясняющих движения планет. И я полагаю, что геометрия Евклида была не просто очерком чистой геометрии (как обычно считают), а органоном теории мира. С этой точки зрения, «Элементы» были не «учебником по геометрии», а попыткой систематического решения основных проблем космологии Платона. Это было осуществлено столь успешно, что решённые проблемы ушли в тень и оказались почти забытыми. Какой-то их след сохранился у Прокла, который пишет: «Некоторые думали, что содержание разнообразных книг (Евклида) имеет отношение к космосу и что они были предназначены для того, чтобы изучать универсум» (op. cit., прим. 38 выше, Prologus, II, p. 71, 2–5).

Однако даже Прокл не упоминает в этом контексте о главной проблеме — проблеме иррациональности (он, конечно, упоминает о ней в других местах), хотя и указывает, что «Элементы» явились высшим достижением в построении «космических» или «платонических» правильных многогранников. Именно со времён ⁴⁶ Платона и Евклида, но не ранее, геометрия (а не арифметика) становится наиболее важным инструментом всех физических объяснений и описаний как в теории материи, так и в космологии ⁴⁷.

Часть IX

Таковы исторические факты. Я полагаю, они в достаточной мере обосновывают мой главный тезис: prima facie метод изучения философии не способен дать подлинного понимания тех проблем, которые стимулировали Платона. И этот метод не способен привести к правильной оценке его наиболее важного философского достижения — геометрической теории мира. Крупнейшие физики Возрождения — Коперник, Галилей, Кеплер, Гилберт, — обратившиеся от Аристотеля к Платону, стремились заменить аристотелевские качественные субстанции или потенциальности геометрическим методом космологии. Действительно, (в науке) Возрождение означало возрождение геометрического метода, лежащего в основе деятельности Евклида, Аристарха, Архимеда, Коперника, Кеплера, Галилея, Декарта, Ньютона, Максвелла и Эйнштейна.

Но можно ли считать это достижение собственно философским? Не относится ли оно скорее к физике — фактуальной науке или к чистой математике — разделу тавтологичной логики, как считает школа Витгенштейна?

Я полагаю, что теперь мы достаточно ясно можем увидеть, почему достижение Платона (хотя оно, без сомнения, включало в себя физические, логические и смешанные компоненты) было именно философским, почему по крайней мере часть его философии природы и физики сохранилась до сих пор и, я думаю, будет сохраняться в дальнейшем.

У Платона и его предшественников мы находим сознательное построение и изобретение нового подхода к миру и его познанию.

Первоначальную теологическую идею объяснения видимого мира с помощью постулируемого невидимого мира этот подход преобразует в наиболее важный инструмент теоретической науки. Эта идея в явном виде была сформулирована Анаксагором и Демокритом ⁴⁹ в качестве принципа изучения природы материи или материальных тел. Видимая материя объясняется посредством гипотез, говорящих о невидимом, о невидимой структуре, которая слишком мала, чтобы её можно было видеть. Платон принимает и обобщает эту идею: изменчивый видимый мир объясняется посредством невидимого мира неизменных «форм» (субстанций, сущностей или «природ»; то есть, как я пытаюсь показать, посредством геометрических образов или фигур).

Является ли эта идея относительно невидимой структуры материи физической или философской? Если физик лишь действует в русле этой теории, если он, возможно неосознанно, принимает её, побуждаемый к этому собственной проблемной ситуацией, и если при этом он создаёт новую конкретную теорию структуры материи, то я не могу назвать его философом. Но если он размышляет над этой идеей и, например, отвергает её (подобно Беркли или Маху), предпочитая феноменологическую или позитивистскую физику теоретическому и отчасти теологическому подходу, то его можно назвать философом. И точно так же тот, кто сознательно избирает теоретический подход, разрабатывает его и выражает в явном виде, перенося тем самым гипотетический и дедуктивный метод из теологии в физику, будет философом, даже если в качестве физика он пытается создавать конкретные теории невидимой структуры материи.

Однако я не буду больше заниматься вопросом о правильном употреблении слова «философия», ибо это — проблема Витгенштейна и очевидно относится к употреблению языка. Здесь мы имеем дело с типичной псевдопроблемой, обсуждение которой не может принести ничего, кроме скуки.

Теперь мне хочется добавить несколько слов относительно теории форм или идей Платона, точнее, относительно пункта (6) данного выше списка исторических фактов.

Теорию структуры материи Платона можно найти в «Тимее». Она имеет внешнее сходство с современной теорией твёрдых тел, истолковывающей их как кристаллы. Физические тела у Платона составлены из невидимых элементарных частиц различного вида. Видом этих частиц обусловлены макроскопические свойства видимой материи. Вид же элементарных частиц, в свою очередь, детерминирован видом плоских фигур, образующих их стороны. Наконец, сами эти плоские фигуры все состоят из двух элементарных треугольников: равнобедренного прямоугольного треугольника (половина квадрата), содержащего квадратный корень из двух, и прямоугольного треугольника (половина прямоугольника), содержащего квадратный корень из трех, то есть иррациональные величины.

Эти треугольники считаются копиями ⁵⁰ неизменных «форм» или «идей». Это означает, что геометрические «формы» включаются в сферу пифагорейских арифметических форм-чисел.

Трудно сомневаться в том, что побудительным мотивом этого построения было стремление преодолеть кризис атомизма посредством включения иррациональностей в конечные элементы мира. Как только это было сделано, затруднение, вызванное существованием иррациональных расстояний, исчезло.

Но почему Платон избрал именно эти два вида треугольников? В другом месте ⁵¹ я высказал предположение о том, что Платон верил, будто все другие иррациональности можно получить посредством рационального умножения квадратных корней из двух или трёх ⁵². Теперь я думаю, что это не вытекает из наиболее важного отрывка из «Тимея» (это неверно, как впоследствии показал Евклид). В упомянутом отрывке Платон говорит совершенно ясно: «Все треугольники выводимы из двух, имеющих прямой угол», и характеризует эти два треугольника как полу-квадрат и полу-прямоугольник. Однако в его контексте это может означать лишь, что все треугольники можно представить как комбинацию этих двух треугольников. Такая точка зрения эквивалентна ошибочной теории относительно соизмеримости всех иррациональных величин и суммы рационального числа с квадратными корнями из двух и трёх ⁵³.

Однако Платон не претендовал на доказательство этой теории. Напротив, он отмечал, что принимает эти два треугольника в качестве принципов, «в соответствии с подходом, соединяющим предполагаемое с необходимым». А несколько ниже, после утверждения о том, что полу-прямоугольный треугольник он принимает в качестве второго принципа, он говорит: «Слишком долго рассказывать о причинах, но если кто-то захочет заняться этим вопросом и доказать, что он обладает этим свойством (я думаю, тем свойством, что все другие треугольники можно составить из этих двух), то мы охотно отдадим ему награду» ⁵⁴. Язык несколько темен, и можно допустить, что Платон осознавал отсутствие доказательства его (ошибочного) предположения относительно этих двух треугольников и надеялся, что кто-то его предложит.

Неясность этого отрывка привела к странному следствию.

Большинство читателей и комментаторов Платона не заметили, что избранные им треугольники вводят иррациональности в его мир форм, хотя в других местах Платон подчёркивает важность проблемы иррациональности.

Возможно, это объясняет, почему теория форм Платона могла показаться Аристотелю по существу аналогичной пифагорейской теории форм-чисел ⁵⁵ и почему атомизм Платона показался Аристотелю лишь вариантом атомизма Демокрита ⁵⁶.

Несмотря на то что Аристотель ассоциировал арифметику с чётным и нечётным, а геометрию — с иррациональным, он не воспринимал проблему иррациональности всерьёз. Опираясь на интерпретацию «Тимея», отождествлявшую платоновское Пространство с материей, Аристотель, по-видимому, считал платоновскую программу реформы геометрии выполненной. Отчасти это было осуществлено Евдоксом ещё до того, как Аристотель пришёл в Академию, а сам он лишь весьма поверхностно интересовался математикой. Он нигде не упоминает о надписи над воротами Академии.

Подводя итоги сказанному, можно предположить, что теория форм Платона и его теория материи были обновлением теорий его предшественников — пифагорейцев и Демокрита — в свете осознания им того факта, что иррациональности требуют поставить геометрию впереди арифметики. Содействуя этому, Платон внёс важный вклад в разработку системы Евклида — самой влиятельной из всех когда-либо созданных дедуктивных систем. Приняв геометрию в качестве теории мира, он проложил путь для творчества Аристарха, Ньютона и Эйнштейна. Благодаря этому кризис греческого атомизма был преобразован в фундаментальное достижение. Однако научные интересы Платона в значительной мере оказались забытыми. Ситуация в науке, породившая его философские проблемы, была плохо понята. А его величайшее достижение — геометрическая теория мира — до такой степени влияла на наше представление о мире, что мы неосознанно считали эту теорию несомненной.

Часть X

Одного примера всегда недостаточно. Из громадного множества интересных возможностей я избираю в качестве второго примера Канта.

Его «Критика чистого разума» является одной из наиболее сложных из когда-либо написанных книг. Кант работал в великой спешке ⁵⁷ и размышлял над проблемой, которая, как я попытаюсь показать, была не только неразрешима, но и неправильно понята. Тем не менее это была не псевдопроблема, ибо она была порождена реальной ситуацией, сложившейся в науке.

Его книга была написана для тех, кто кое-что знал о небесной механике Ньютона и имел какое-то представление о его предшественниках — о Копернике, Тихо Браге, Кеплере и Галилее.

Просвещённым людям нашего времени, избалованным зрелищем непрерывных успехов науки, трудно понять, чем была теория Ньютона не только для Канта, но для любого мыслителя восемнадцатого столетия. После эпохи безудержной смелости, с которой древние штурмовали загадки природы, наступил длительный период упадка и постепенного возрождения. Ньютон открыл новый путь к успехам. Его геометрическая теория, опиравшаяся на работу Евклида, первоначально вызывала большое недоверие, причём даже у её собственного создателя ⁵⁸.

Причина заключалась в том, что сила гравитационного притяжения казалась чем-то «оккультным» и во всяком случае нуждалась в объяснении. Несмотря на то что приемлемого объяснения так и не нашли (а Ньютон не хотел прибегать к ad hoc гипотезам), все опасения в отношении его теории рассеялись задолго до того, как Кант внёс в неё собственный важный вклад. Это случилось через семьдесят восемь лет после выхода в свет «Principia» ⁵⁹. Ни один образованный человек ⁶⁰ не мог больше сомневаться в том, что теория Ньютона истинна. Для её проверки использовались самые точные измерения, но она всегда оказывалась права. Она предсказала небольшие отклонения от законов Кеплера и иные новые открытия. В наше время, когда теории приходят и уходят подобно автобусам на Пиккадилли и когда каждый школьник слышал о том, что Эйнштейн давно превзошёл Ньютона, трудно понять то чувство уверенности, восторга и свободы, которое внушала теория Ньютона. В истории человеческого мышления произошло уникальное событие, которое уже никогда не может повториться: первое и последнее открытие абсолютной истины о мире. Тысячелетняя мечта осуществилась. Человечество получило знание — реальное, несомненное и доказанное знание, божественную scientia или episteme, а не только doxa, человеческое мнение.

Таким образом, для Канта теория Ньютона была просто истинной, и убеждение в её истинности сохранялось в течение столетия после смерти Канта. В конце концов Кант признал, что он и все другие лишь считали её scientia или episteme. Вначале он принимал эту теорию без каких бы то ни было сомнений. Это состояние он назвал своим «догматическим сном». Разбужен он был Юмом.

Юм учил, что несомненного знания универсальных законов, или episteme, не может существовать; что всё наше знание получено с помощью наблюдения, которое относится только к единичным вещам, поэтому всё теоретическое знание недостоверно. Его аргументы были убедительны (и он, конечно, был прав). Однако существовал факт или то, что казалось фактом, — получение Ньютоном episteme.

Юм заставил Канта усомниться в том, что он считал фактом. Здесь была проблема, от которой нельзя было отмахнуться. Как мог бы человек получить знание? Знание, которое было бы общим, точным, математическим, доказуемым и бесспорным, подобно Евклидовой геометрии, и вместе с тем давать каузальное объяснение наблюдаемым фактам?

Так возникает центральная проблема «Критики чистого разума»: «Как возможно чистое естествознание?» Под «чистым естествознанием» — scientia, episteme — Кант подразумевает просто теорию Ньютона. (К сожалению, сам он об этом не сказал, и я не понимаю, каким образом студент, читающий его первую «Критику» в 1781 и 1787 годах, мог бы обнаружить это. Но то, что Кант имел в виду именно теорию Ньютона, выясняется из «Метафизических оснований естествознания», 1786 году, где он даёт априорную дедукцию теории Ньютона; см. восемь теорем Второй главной части и Приложение 2, замечание 1, параграф 2.) В пяти параграфах заключительного «Общего замечания о феноменологии» Кант относит теорию Ньютона к «звёздному небу». Это можно увидеть также из «Заключения» к «Критике практического разума», 1788 года, где обращение к «звёздному небу» поясняется ссылкой на априорный характер новой астрономии ⁶¹.

Хотя «Критика» была написана плохим языком и отличалась громоздким стилем, эта проблема не могла быть сведена к лингвистической головоломке. Существовало знание. Каким образом Ньютон смог получить его? Нельзя было уйти от этого вопроса ⁶². Однако он был неразрешим, ибо кажущийся факт получения episteme был реальным фактом.

Как нам теперь известно или кажется, что известно, теория Ньютона была лишь изумительным предположением, удивительно хорошим приближением. Она действительно была уникальна, но не как божественная истина, а как уникальное достижение человеческого гения, она представляла собой не episteme, а лишь doxa. Поэтому-то и рушится кантовская проблема «Как возможно чистое естествознание?» и исчезает большая часть волновавших его трудностей.

Предложенное Кантом решение его неразрешимой проблемы заключалось в том, что он с гордостью назвал «копер-никанской революцией», совершенной им в теории познания. Знание — episteme — возможно потому, что мы не пассивно воспринимаем данные органов чувств, а активно перерабатываем их. Ассимилируя и перерабатывая их, мы образуем из них Космос, мир природы. На материал, предоставляемый нашими чувствами, мы налагаем математические законы, являющиеся частью нашего организующего механизма. Таким образом, наш разум не открывает универсальные законы в природе, а предписывает ей свои собственные законы, налагает их на природу.

Эта теория представляет собой странную смесь абсурда и истины. Она абсурдна, ибо пытается решить неправильно поставленную проблему и доказывает слишком много, стремясь и доказать слишком много. Согласно теории Канта, «чистое естествознание» не просто возможно. Хотя он не всегда осознает это, но вопреки его намерениям оно оказывается необходимым результатом нашей мыслительной деятельности. Если факт получения нами episteme можно объяснить посредством того факта, что наш разум создаёт и налагает свои собственные законы на природу, то первый из двух фактов не может быть более случайным, чем второй ⁶³. Таким образом, проблема заключается не в том, как смог Ньютон совершить своё открытие, а в том, как можно было бы не совершить его. Почему наш интеллектуальный механизм не работал раньше?

В этом заключается очевидно абсурдное следствие идеи Канта. Однако было бы не вполне правомерно просто отбросить её и саму проблему как псевдопроблему. В идее Канта мы можем обнаружить зерно истины (как и в некоторых воззрениях Юма) после того, как надлежащим образом сформулируем его проблему. Как нам теперь известно (или мы считаем, что известно), его вопрос должен звучать так: «Как возможны успешные предположения?» И в духе его «коперниканской революции» наш ответ, как мне кажется, может быть таким: потому что мы, как вы сказали, являемся не пассивными регистраторами чувственных данных, а активными организмами. Потому что на наше окружение мы реагируем не только инстинктивно, но иногда сознательно и свободно. Потому что мы способны изобретать мифы и теории, стремимся к объяснению, хотим знать. Потому что мы не только изобретаем мифы и теории, но стремимся узнать, работают ли они и как работают. Потому что за счёт огромных усилий и преодоления множества ошибок иногда, в случае удачи, мы создаём такой сюжет, такое объяснение, которое «спасает феномены», например, миф о «невидимых» вещах, скажем, атомах или силах гравитации, объясняющий видимое. Потому что познание есть приключение идей.

Верно, что эти идеи создаются нами, а не окружающим миром, они представляют собой не просто следы повторяющихся впечатлений или стимулов. В этом вы правы. Но мы даже более активны и свободны, чем думали вы, ибо сходные наблюдения или похожие ситуации не приводят, как следует из вашей теории, к одинаковым объяснениям у разных людей. И успешность наших теорий ⁶⁴ объясняется вовсе не тем, что мы сами создаём их и пытаемся налагать на природу. Подавляющее большинство наших теорий, свободно изобретаемых нами идей оказываются безуспешными, они не выдерживают проверки и отбрасываются как фальсифицированные опытом. И лишь очень немногие из них, да и то на время, добиваются успеха в борьбе за выживание ⁶⁵.

Часть XI

Немногие из последователей Канта имели ясное представление о той проблемной ситуации, которая стимулировала его деятельность.

Перед ним стояли две проблемы: небесная механика Ньютона и абсолютные стандарты человеческого братства и справедливости, к которым апеллировала Французская революция, или, как выразился сам Кант, «звёздное небо надо мной и моральный закон во мне». Однако редко понимают, чем было «звёздное небо» Канта — напоминанием о Ньютоне ⁶⁶. Начиная с Фихте ⁶⁷, многие пытались копировать «метод» Канта и сложный стиль его «Критики». Однако большинство этих имитаторов, не понимая первоначальных интересов и проблем Канта, бессмысленно пытались распутать тот гордиев узел, в котором Кант, хотя и не по своей вине, запутался сам.

Следует опасаться бессмысленных и бесплодных тонкостей, которыми имитаторы обволакивают подлинную проблему первопроходца.

Нужно помнить о том, что хотя его проблема и не была эмпирической в обыденном смысле, тем не менее неожиданно оказалась в каком-то смысле фактуальной (Кант называл такие факты «трансцендентальными»), ибо была порождена кажущимся, хотя реально не существующим, примером scientia или episteme. И я полагаю, что следует серьёзно рассмотреть предположение о том, что ответ Канта, несмотря на его частичную абсурдность, содержит зерно истинной философии науки.